Towards Decentralized and Sustainable Foundation Model Training with the Edge

Foundation models are at the forefront of AI research, appealing for their ability to learn from vast datasets and cater to diverse tasks. Yet, their significant computational demands raise issues of environmental impact and the risk of centralized control in their development. We put forward a vision towards decentralized and sustainable foundation model training that leverages the collective compute of sparingly used connected edge AI devices. We present the rationale behind our vision, particularly in support of its sustainability benefit. We further outline a set of challenges that need to be addressed to turn this vision into reality.

Masked Matrix Multiplication for Emergent Sparsity

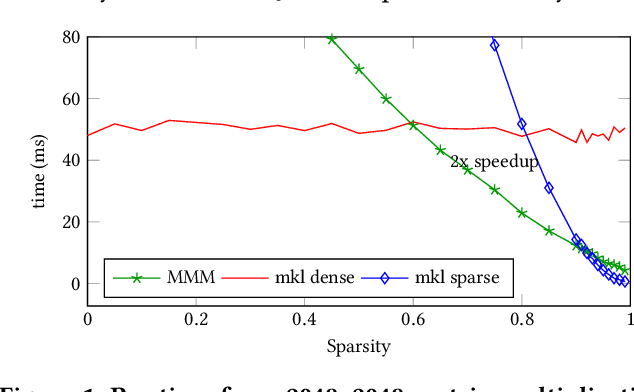
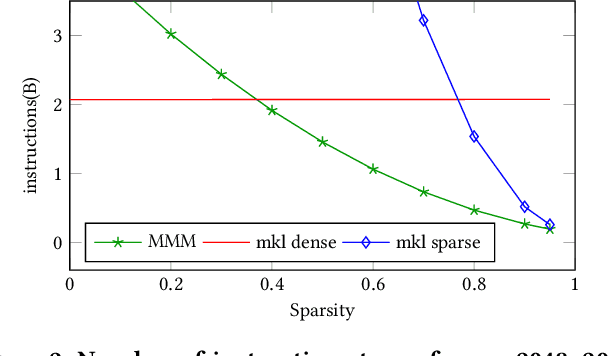
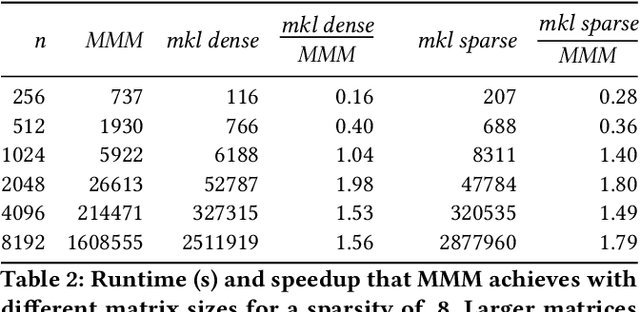
Artificial intelligence workloads, especially transformer models, exhibit emergent sparsity in which computations perform selective sparse access to dense data. The workloads are inefficient on hardware designed for dense computations and do not map well onto sparse data representations. We build a vectorized and parallel matrix-multiplication system A X B = C that eliminates unnecessary computations and avoids branches based on a runtime evaluation of sparsity. We use a combination of dynamic code lookup to adapt to the specific sparsity encoded in the B matrix and preprocessing of sparsity maps of the A and B matrices to compute conditional branches once for the whole computation. For a wide range of sparsity, from 60% to 95% zeros, our implementation performs fewer instructions and increases performance when compared with Intel MKL's dense or sparse matrix multiply routines. Benefits can be as large as 2 times speedup and 4 times fewer instructions.

Prospective Learning: Back to the Future

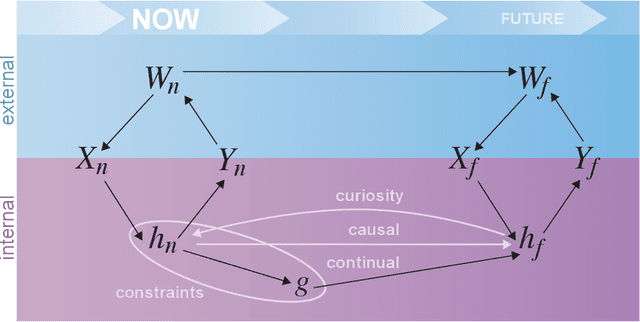
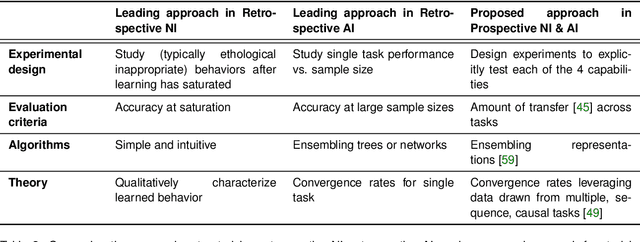
Research on both natural intelligence (NI) and artificial intelligence (AI) generally assumes that the future resembles the past: intelligent agents or systems (what we call 'intelligence') observe and act on the world, then use this experience to act on future experiences of the same kind. We call this 'retrospective learning'. For example, an intelligence may see a set of pictures of objects, along with their names, and learn to name them. A retrospective learning intelligence would merely be able to name more pictures of the same objects. We argue that this is not what true intelligence is about. In many real world problems, both NIs and AIs will have to learn for an uncertain future. Both must update their internal models to be useful for future tasks, such as naming fundamentally new objects and using these objects effectively in a new context or to achieve previously unencountered goals. This ability to learn for the future we call 'prospective learning'. We articulate four relevant factors that jointly define prospective learning. Continual learning enables intelligences to remember those aspects of the past which it believes will be most useful in the future. Prospective constraints (including biases and priors) facilitate the intelligence finding general solutions that will be applicable to future problems. Curiosity motivates taking actions that inform future decision making, including in previously unmet situations. Causal estimation enables learning the structure of relations that guide choosing actions for specific outcomes, even when the specific action-outcome contingencies have never been observed before. We argue that a paradigm shift from retrospective to prospective learning will enable the communities that study intelligence to unite and overcome existing bottlenecks to more effectively explain, augment, and engineer intelligences.

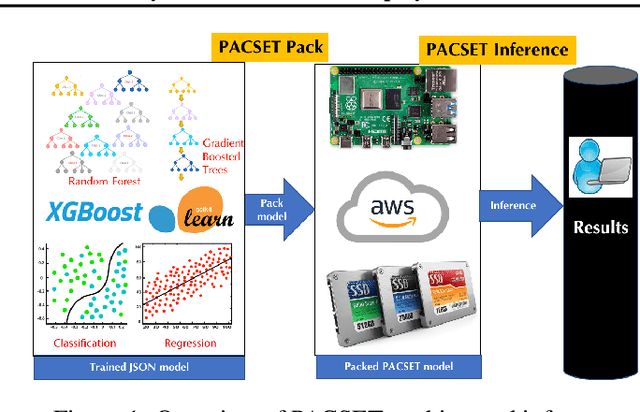
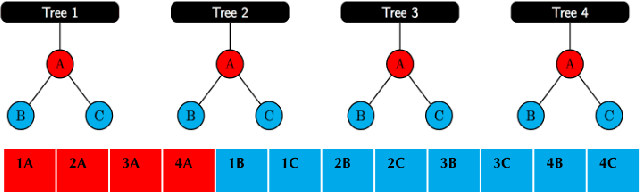
PACSET (Packed Serialized Trees): Reducing Inference Latency for Tree Ensemble Deployment

We present methods to serialize and deserialize tree ensembles that optimize inference latency when models are not already loaded into memory. This arises whenever models are larger than memory, but also systematically when models are deployed on low-resource devices, such as in the Internet of Things, or run as Web micro-services where resources are allocated on demand. Our packed serialized trees (PACSET) encode reference locality in the layout of a tree ensemble using principles from external memory algorithms. The layout interleaves correlated nodes across multiple trees, uses leaf cardinality to collocate the nodes on the most popular paths and is optimized for the I/O blocksize. The result is that each I/O yields a higher fraction of useful data, leading to a 2-6 times reduction in classification latency for interactive workloads.

Geodesic Learning via Unsupervised Decision Forests

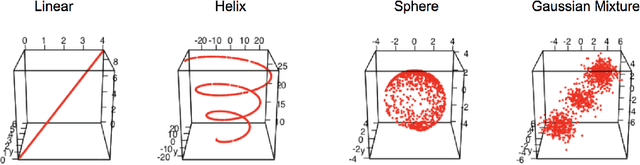
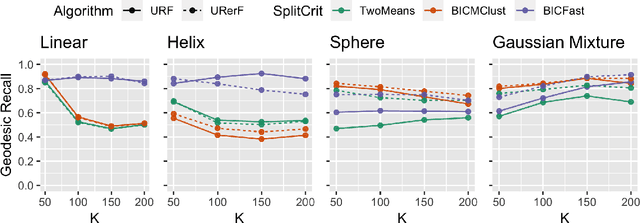
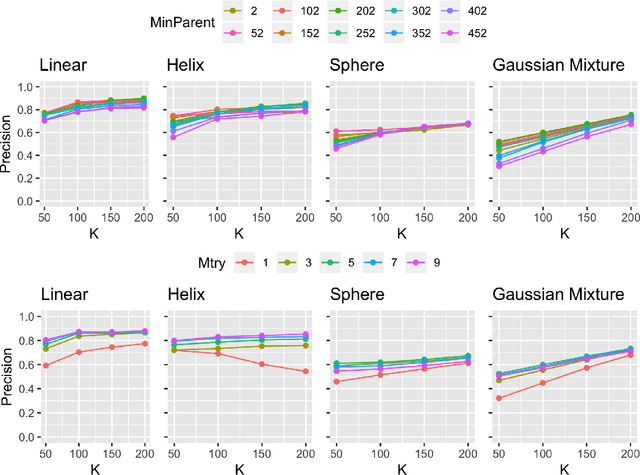
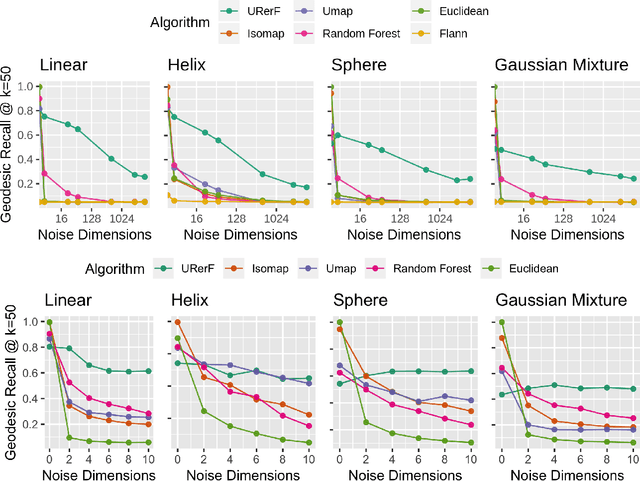
Geodesic distance is the shortest path between two points in a Riemannian manifold. Manifold learning algorithms, such as Isomap, seek to learn a manifold that preserves geodesic distances. However, such methods operate on the ambient dimensionality, and are therefore fragile to noise dimensions. We developed an unsupervised random forest method (URerF) to approximately learn geodesic distances in linear and nonlinear manifolds with noise. URerF operates on low-dimensional sparse linear combinations of features, rather than the full observed dimensionality. To choose the optimal split in a computationally efficient fashion, we developed a fast Bayesian Information Criterion statistic for Gaussian mixture models. We introduce geodesic precision-recall curves which quantify performance relative to the true latent manifold. Empirical results on simulated and real data demonstrate that URerF is robust to high-dimensional noise, where as other methods, such as Isomap, UMAP, and FLANN, quickly deteriorate in such settings. In particular, URerF is able to estimate geodesic distances on a real connectome dataset better than other approaches.

Inferring Concept Prerequisite Relations from Online Educational Resources

The Internet has rich and rapidly increasing sources of high quality educational content. Inferring prerequisite relations between educational concepts is required for modern large-scale online educational technology applications such as personalized recommendations and automatic curriculum creation. We present PREREQ, a new supervised learning method for inferring concept prerequisite relations. PREREQ is designed using latent representations of concepts obtained from the Pairwise Latent Dirichlet Allocation model, and a neural network based on the Siamese network architecture. PREREQ can learn unknown concept prerequisites from course prerequisites and labeled concept prerequisite data. It outperforms state-of-the-art approaches on benchmark datasets and can effectively learn from very less training data. PREREQ can also use unlabeled video playlists, a steadily growing source of training data, to learn concept prerequisites, thus obviating the need for manual annotation of course prerequisites.