Leyla Isik
Teresa
Simple 3D Pose Features Support Human and Machine Social Scene Understanding
Nov 06, 2025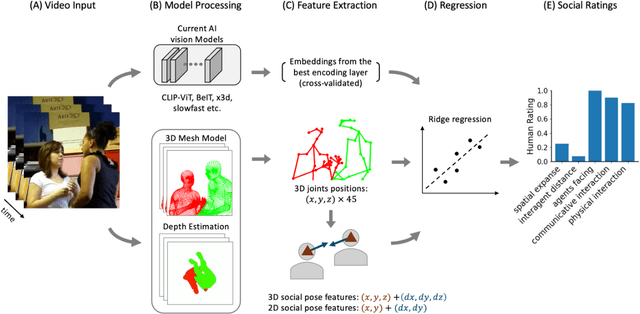
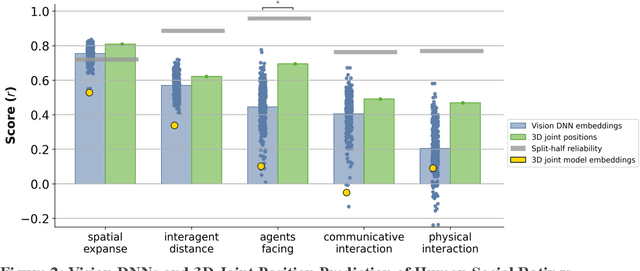
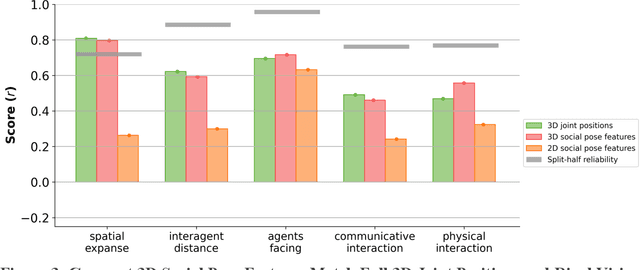
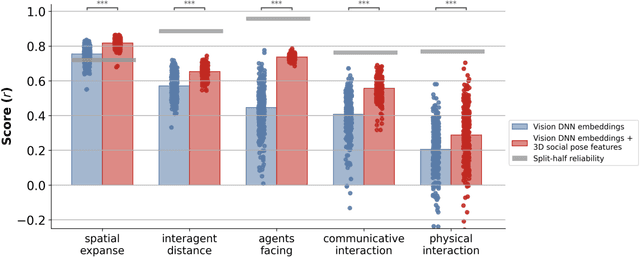
Abstract:Humans can quickly and effortlessly extract a variety of information about others' social interactions from visual input, ranging from visuospatial cues like whether two people are facing each other to higher-level information. Yet, the computations supporting these abilities remain poorly understood, and social interaction recognition continues to challenge even the most advanced AI vision systems. Here, we hypothesized that humans rely on 3D visuospatial pose information to make social interaction judgments, which is absent in most AI vision models. To test this, we combined state-of-the-art pose and depth estimation algorithms to extract 3D joint positions of people in short video clips depicting everyday human actions and compared their ability to predict human social interaction judgments with current AI vision models. Strikingly, 3D joint positions outperformed most current AI vision models, revealing that key social information is available in explicit body position but not in the learned features of most vision models, including even the layer-wise embeddings of the pose models used to extract joint positions. To uncover the critical pose features humans use to make social judgments, we derived a compact set of 3D social pose features describing only the 3D position and direction of faces in the videos. We found that these minimal descriptors matched the predictive strength of the full set of 3D joints and significantly improved the performance of off-the-shelf AI vision models when combined with their embeddings. Moreover, the degree to which 3D social pose features were represented in each off-the-shelf AI vision model predicted the model's ability to match human social judgments. Together, our findings provide strong evidence that human social scene understanding relies on explicit representations of 3D pose and can be supported by simple, structured visuospatial primitives.
Aligning Video Models with Human Social Judgments via Behavior-Guided Fine-Tuning
Oct 01, 2025Abstract:Humans intuitively perceive complex social signals in visual scenes, yet it remains unclear whether state-of-the-art AI models encode the same similarity structure. We study (Q1) whether modern video and language models capture human-perceived similarity in social videos, and (Q2) how to instill this structure into models using human behavioral data. To address this, we introduce a new benchmark of over 49,000 odd-one-out similarity judgments on 250 three-second video clips of social interactions, and discover a modality gap: despite the task being visual, caption-based language embeddings align better with human similarity than any pretrained video model. We close this gap by fine-tuning a TimeSformer video model on these human judgments with our novel hybrid triplet-RSA objective using low-rank adaptation (LoRA), aligning pairwise distances to human similarity. This fine-tuning protocol yields significantly improved alignment with human perceptions on held-out videos in terms of both explained variance and odd-one-out triplet accuracy. Variance partitioning shows that the fine-tuned video model increases shared variance with language embeddings and explains additional unique variance not captured by the language model. Finally, we test transfer via linear probes and find that human-similarity fine-tuning strengthens the encoding of social-affective attributes (intimacy, valence, dominance, communication) relative to the pretrained baseline. Overall, our findings highlight a gap in pretrained video models' social recognition and demonstrate that behavior-guided fine-tuning shapes video representations toward human social perception.
Using Multimodal Deep Neural Networks to Disentangle Language from Visual Aesthetics
Oct 31, 2024



Abstract:When we experience a visual stimulus as beautiful, how much of that experience derives from perceptual computations we cannot describe versus conceptual knowledge we can readily translate into natural language? Disentangling perception from language in visually-evoked affective and aesthetic experiences through behavioral paradigms or neuroimaging is often empirically intractable. Here, we circumnavigate this challenge by using linear decoding over the learned representations of unimodal vision, unimodal language, and multimodal (language-aligned) deep neural network (DNN) models to predict human beauty ratings of naturalistic images. We show that unimodal vision models (e.g. SimCLR) account for the vast majority of explainable variance in these ratings. Language-aligned vision models (e.g. SLIP) yield small gains relative to unimodal vision. Unimodal language models (e.g. GPT2) conditioned on visual embeddings to generate captions (via CLIPCap) yield no further gains. Caption embeddings alone yield less accurate predictions than image and caption embeddings combined (concatenated). Taken together, these results suggest that whatever words we may eventually find to describe our experience of beauty, the ineffable computations of feedforward perception may provide sufficient foundation for that experience.
How does the primate brain combine generative and discriminative computations in vision?
Jan 11, 2024Abstract:Vision is widely understood as an inference problem. However, two contrasting conceptions of the inference process have each been influential in research on biological vision as well as the engineering of machine vision. The first emphasizes bottom-up signal flow, describing vision as a largely feedforward, discriminative inference process that filters and transforms the visual information to remove irrelevant variation and represent behaviorally relevant information in a format suitable for downstream functions of cognition and behavioral control. In this conception, vision is driven by the sensory data, and perception is direct because the processing proceeds from the data to the latent variables of interest. The notion of "inference" in this conception is that of the engineering literature on neural networks, where feedforward convolutional neural networks processing images are said to perform inference. The alternative conception is that of vision as an inference process in Helmholtz's sense, where the sensory evidence is evaluated in the context of a generative model of the causal processes giving rise to it. In this conception, vision inverts a generative model through an interrogation of the evidence in a process often thought to involve top-down predictions of sensory data to evaluate the likelihood of alternative hypotheses. The authors include scientists rooted in roughly equal numbers in each of the conceptions and motivated to overcome what might be a false dichotomy between them and engage the other perspective in the realm of theory and experiment. The primate brain employs an unknown algorithm that may combine the advantages of both conceptions. We explain and clarify the terminology, review the key empirical evidence, and propose an empirical research program that transcends the dichotomy and sets the stage for revealing the mysterious hybrid algorithm of primate vision.
Out-of-distribution and in-distribution posterior calibration using Kernel Density Polytopes
Feb 14, 2022

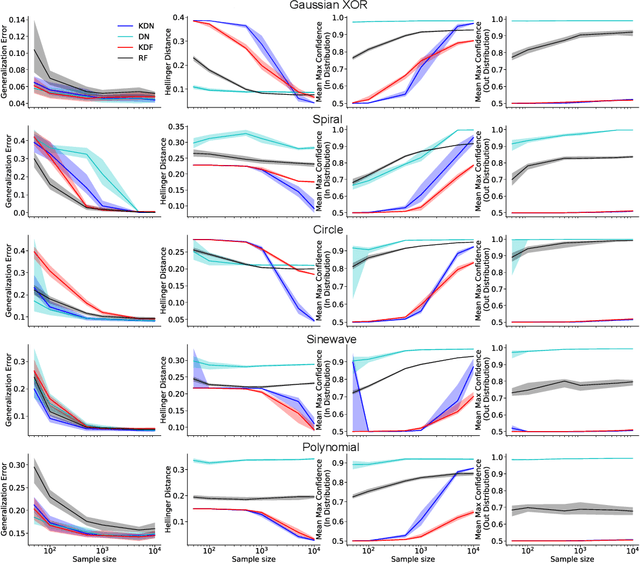
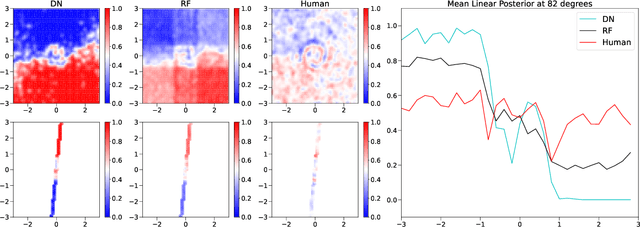
Abstract:Any reasonable machine learning (ML) model should not only interpolate efficiently in between the training samples provided (in-distribution region), but also approach the extrapolative or out-of-distribution (OOD) region without being overconfident. Our experiment on human subjects justifies the aforementioned properties for human intelligence as well. Many state-of-the-art algorithms have tried to fix the overconfidence problem of ML models in the OOD region. However, in doing so, they have often impaired the in-distribution performance of the model. Our key insight is that ML models partition the feature space into polytopes and learn constant (random forests) or affine (ReLU networks) functions over those polytopes. This leads to the OOD overconfidence problem for the polytopes which lie in the training data boundary and extend to infinity. To resolve this issue, we propose kernel density methods that fit Gaussian kernel over the polytopes, which are learned using ML models. Specifically, we introduce two variants of kernel density polytopes: Kernel Density Forest (KDF) and Kernel Density Network (KDN) based on random forests and deep networks, respectively. Studies on various simulation settings show that both KDF and KDN achieve uniform confidence over the classes in the OOD region while maintaining good in-distribution accuracy compared to that of their respective parent models.
Prospective Learning: Back to the Future
Jan 19, 2022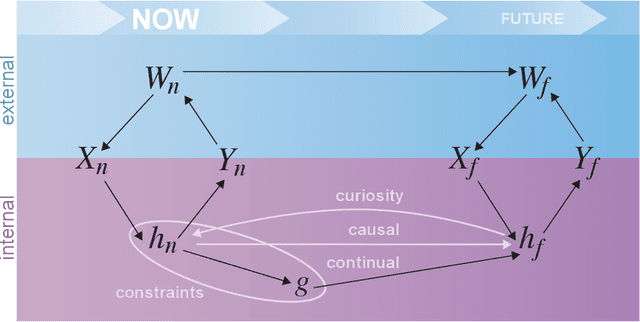

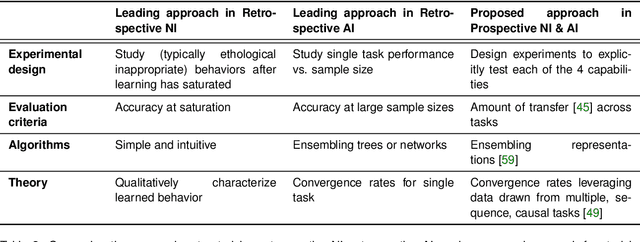
Abstract:Research on both natural intelligence (NI) and artificial intelligence (AI) generally assumes that the future resembles the past: intelligent agents or systems (what we call 'intelligence') observe and act on the world, then use this experience to act on future experiences of the same kind. We call this 'retrospective learning'. For example, an intelligence may see a set of pictures of objects, along with their names, and learn to name them. A retrospective learning intelligence would merely be able to name more pictures of the same objects. We argue that this is not what true intelligence is about. In many real world problems, both NIs and AIs will have to learn for an uncertain future. Both must update their internal models to be useful for future tasks, such as naming fundamentally new objects and using these objects effectively in a new context or to achieve previously unencountered goals. This ability to learn for the future we call 'prospective learning'. We articulate four relevant factors that jointly define prospective learning. Continual learning enables intelligences to remember those aspects of the past which it believes will be most useful in the future. Prospective constraints (including biases and priors) facilitate the intelligence finding general solutions that will be applicable to future problems. Curiosity motivates taking actions that inform future decision making, including in previously unmet situations. Causal estimation enables learning the structure of relations that guide choosing actions for specific outcomes, even when the specific action-outcome contingencies have never been observed before. We argue that a paradigm shift from retrospective to prospective learning will enable the communities that study intelligence to unite and overcome existing bottlenecks to more effectively explain, augment, and engineer intelligences.
Computational role of eccentricity dependent cortical magnification
Jun 06, 2014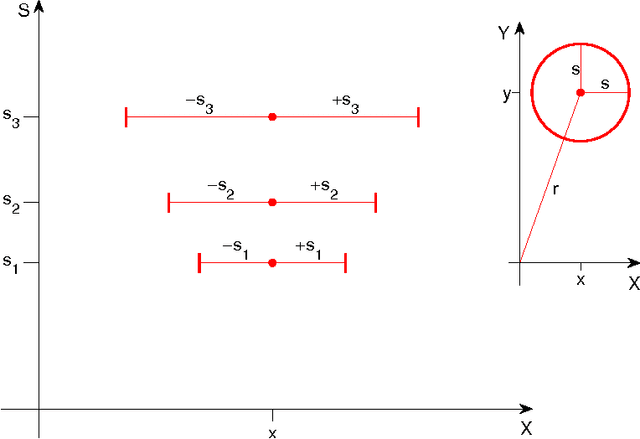
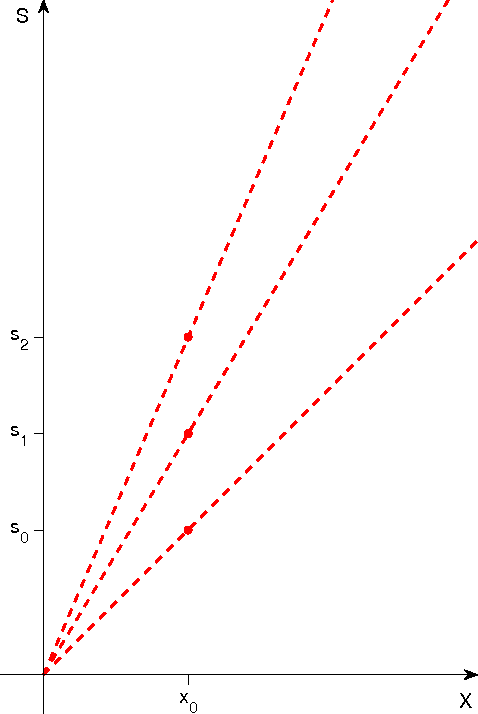
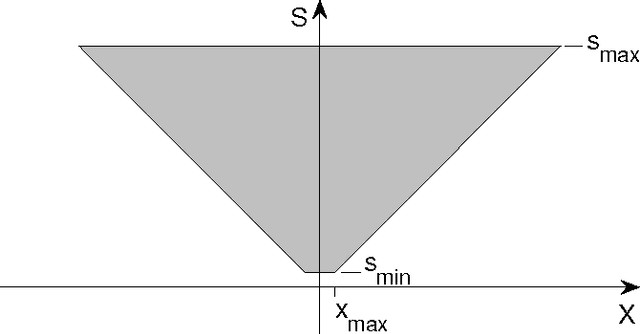
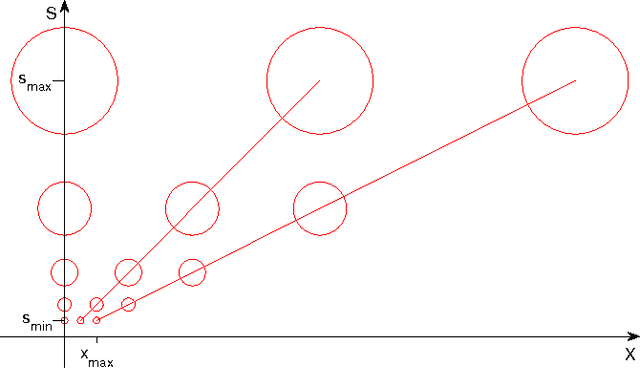
Abstract:We develop a sampling extension of M-theory focused on invariance to scale and translation. Quite surprisingly, the theory predicts an architecture of early vision with increasing receptive field sizes and a high resolution fovea -- in agreement with data about the cortical magnification factor, V1 and the retina. From the slope of the inverse of the magnification factor, M-theory predicts a cortical "fovea" in V1 in the order of $40$ by $40$ basic units at each receptive field size -- corresponding to a foveola of size around $26$ minutes of arc at the highest resolution, $\approx 6$ degrees at the lowest resolution. It also predicts uniform scale invariance over a fixed range of scales independently of eccentricity, while translation invariance should depend linearly on spatial frequency. Bouma's law of crowding follows in the theory as an effect of cortical area-by-cortical area pooling; the Bouma constant is the value expected if the signature responsible for recognition in the crowding experiments originates in V2. From a broader perspective, the emerging picture suggests that visual recognition under natural conditions takes place by composing information from a set of fixations, with each fixation providing recognition from a space-scale image fragment -- that is an image patch represented at a set of increasing sizes and decreasing resolutions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge