Elizabeth L. Ogburn
Teresa
Augmented balancing weights as linear regression
Apr 27, 2023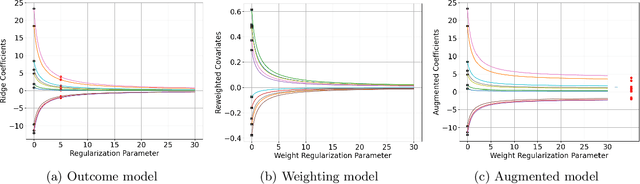
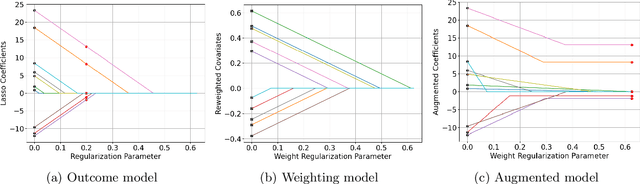
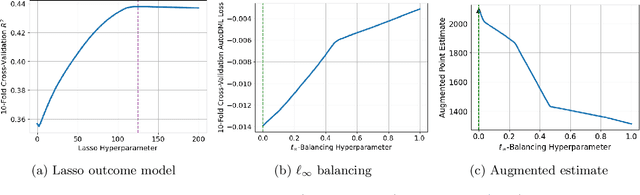
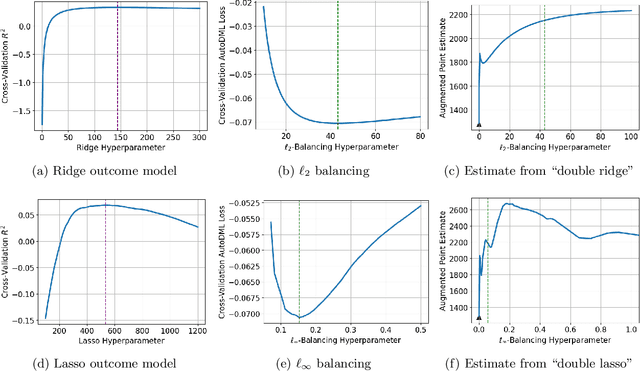
Abstract:We provide a novel characterization of augmented balancing weights, also known as Automatic Debiased Machine Learning (AutoDML). These estimators combine outcome modeling with balancing weights, which estimate inverse propensity score weights directly. When the outcome and weighting models are both linear in some (possibly infinite) basis, we show that the augmented estimator is equivalent to a single linear model with coefficients that combine the original outcome model coefficients and OLS; in many settings, the augmented estimator collapses to OLS alone. We then extend these results to specific choices of outcome and weighting models. We first show that the combined estimator that uses (kernel) ridge regression for both outcome and weighting models is equivalent to a single, undersmoothed (kernel) ridge regression; this also holds when considering asymptotic rates. When the weighting model is instead lasso regression, we give closed-form expressions for special cases and demonstrate a ``double selection'' property. Finally, we generalize these results to linear estimands via the Riesz representer. Our framework ``opens the black box'' on these increasingly popular estimators and provides important insights into estimation choices for augmented balancing weights.
Prospective Learning: Back to the Future
Jan 19, 2022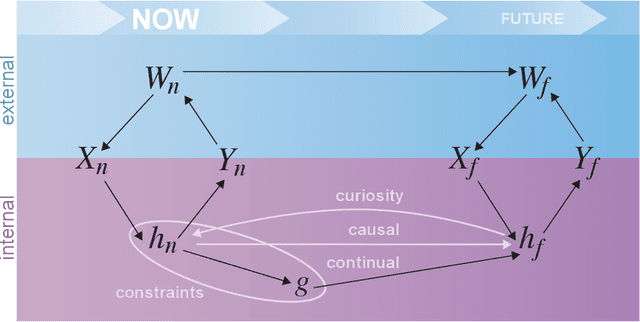

Abstract:Research on both natural intelligence (NI) and artificial intelligence (AI) generally assumes that the future resembles the past: intelligent agents or systems (what we call 'intelligence') observe and act on the world, then use this experience to act on future experiences of the same kind. We call this 'retrospective learning'. For example, an intelligence may see a set of pictures of objects, along with their names, and learn to name them. A retrospective learning intelligence would merely be able to name more pictures of the same objects. We argue that this is not what true intelligence is about. In many real world problems, both NIs and AIs will have to learn for an uncertain future. Both must update their internal models to be useful for future tasks, such as naming fundamentally new objects and using these objects effectively in a new context or to achieve previously unencountered goals. This ability to learn for the future we call 'prospective learning'. We articulate four relevant factors that jointly define prospective learning. Continual learning enables intelligences to remember those aspects of the past which it believes will be most useful in the future. Prospective constraints (including biases and priors) facilitate the intelligence finding general solutions that will be applicable to future problems. Curiosity motivates taking actions that inform future decision making, including in previously unmet situations. Causal estimation enables learning the structure of relations that guide choosing actions for specific outcomes, even when the specific action-outcome contingencies have never been observed before. We argue that a paradigm shift from retrospective to prospective learning will enable the communities that study intelligence to unite and overcome existing bottlenecks to more effectively explain, augment, and engineer intelligences.
Counterexamples to "The Blessings of Multiple Causes" by Wang and Blei
Jan 17, 2020Abstract:This brief note is meant to complement our previous comment on "The Blessings of Multiple Causes" by Wang and Blei (2019). We provide a more succinct and transparent explanation of the fact that the deconfounder does not control for multi-cause confounding. The argument given in Wang and Blei (2019) makes two mistakes: (1) attempting to infer independence conditional on one variable from independence conditional on a different, unrelated variable, and (2) attempting to infer joint independence from pairwise independence. We give two simple counterexamples to the deconfounder claim.
Comment on "Blessings of Multiple Causes"
Oct 17, 2019
Abstract:(This comment has been updated to respond to Wang and Blei's rejoinder [arXiv:1910.07320].) The premise of the deconfounder method proposed in "Blessings of Multiple Causes" by Wang and Blei [arXiv:1805.06826], namely that a variable that renders multiple causes conditionally independent also controls for unmeasured multi-cause confounding, is incorrect. This can be seen by noting that no fact about the observed data alone can be informative about ignorability, since ignorability is compatible with any observed data distribution. Methods to control for unmeasured confounding may be valid with additional assumptions in specific settings, but they cannot, in general, provide a checkable approach to causal inference, and they do not, in general, require weaker assumptions than the assumptions that are commonly used for causal inference. While this is outside the scope of this comment, we note that much recent work on applying ideas from latent variable modeling to causal inference problems suffers from similar issues.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge