Augmented balancing weights as linear regression

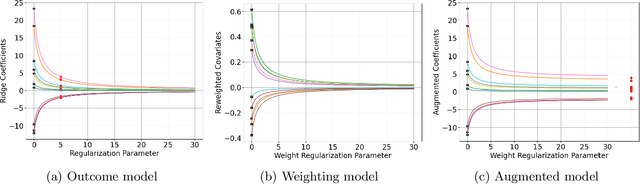
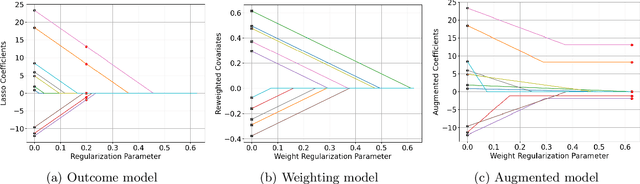
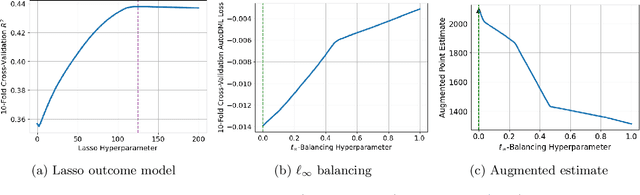
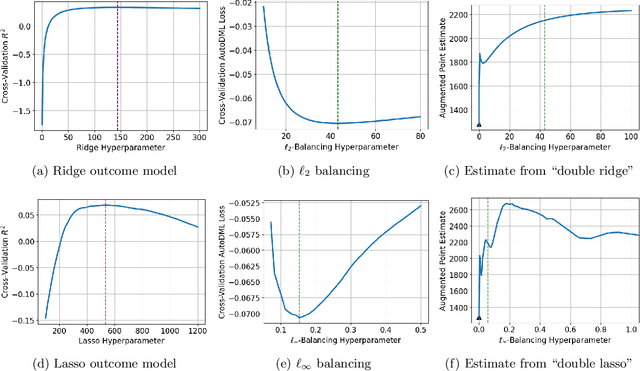
We provide a novel characterization of augmented balancing weights, also known as Automatic Debiased Machine Learning (AutoDML). These estimators combine outcome modeling with balancing weights, which estimate inverse propensity score weights directly. When the outcome and weighting models are both linear in some (possibly infinite) basis, we show that the augmented estimator is equivalent to a single linear model with coefficients that combine the original outcome model coefficients and OLS; in many settings, the augmented estimator collapses to OLS alone. We then extend these results to specific choices of outcome and weighting models. We first show that the combined estimator that uses (kernel) ridge regression for both outcome and weighting models is equivalent to a single, undersmoothed (kernel) ridge regression; this also holds when considering asymptotic rates. When the weighting model is instead lasso regression, we give closed-form expressions for special cases and demonstrate a ``double selection'' property. Finally, we generalize these results to linear estimands via the Riesz representer. Our framework ``opens the black box'' on these increasingly popular estimators and provides important insights into estimation choices for augmented balancing weights.