Deconfounding Scores and Representation Learning for Causal Effect Estimation with Weak Overlap

Overlap, also known as positivity, is a key condition for causal treatment effect estimation. Many popular estimators suffer from high variance and become brittle when features differ strongly across treatment groups. This is especially challenging in high dimensions: the curse of dimensionality can make overlap implausible. To address this, we propose a class of feature representations called deconfounding scores, which preserve both identification and the target of estimation; the classical propensity and prognostic scores are two special cases. We characterize the problem of finding a representation with better overlap as minimizing an overlap divergence under a deconfounding score constraint. We then derive closed-form expressions for a class of deconfounding scores under a broad family of generalized linear models with Gaussian features and show that prognostic scores are overlap-optimal within this class. We conduct extensive experiments to assess this behavior empirically.

Two Approaches to Direct Estimation of Riesz Representers

The Riesz representer is a central object in semiparametric statistics and debiased/doubly-robust estimation. Two literatures in econometrics have highlighted the role for directly estimating Riesz representers: the automatic debiased machine learning literature (as in Chernozhukov et al., 2022b), and an independent literature on sieve methods for conditional moment models (as in Chen et al., 2014). These two literatures solve distinct optimization problems that in the population both have the Riesz representer as their solution. We show that with unregularized or ridge-regularized linear, sieve, or RKHS models, the two resulting estimators are numerically equivalent. However, for other regularization schemes such as the Lasso, or more general machine learning function classes including neural networks, the estimators are not necessarily equivalent. In the latter case, the Chen et al. (2014) formulation yields a novel constrained optimization problem for directly estimating Riesz representers with machine learning. Drawing on results from Birrell et al. (2022), we conjecture that this approach may offer statistical advantages at the cost of greater computational complexity.

Augmented balancing weights as linear regression

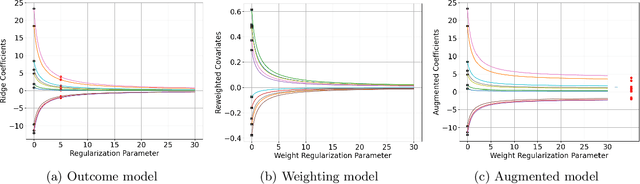
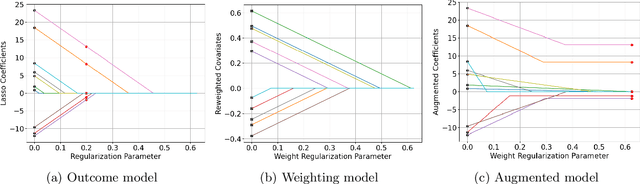
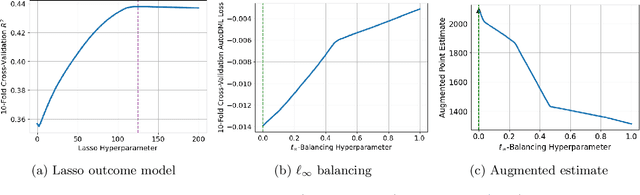
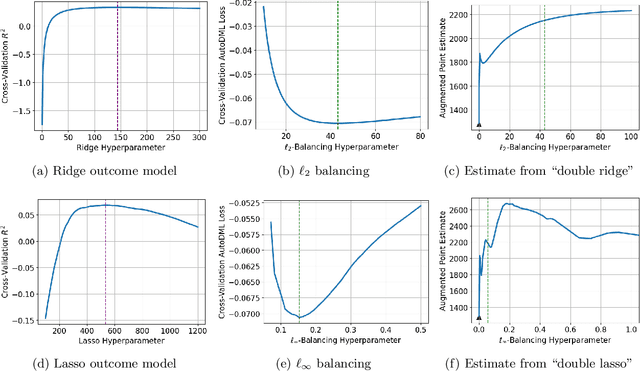
We provide a novel characterization of augmented balancing weights, also known as Automatic Debiased Machine Learning (AutoDML). These estimators combine outcome modeling with balancing weights, which estimate inverse propensity score weights directly. When the outcome and weighting models are both linear in some (possibly infinite) basis, we show that the augmented estimator is equivalent to a single linear model with coefficients that combine the original outcome model coefficients and OLS; in many settings, the augmented estimator collapses to OLS alone. We then extend these results to specific choices of outcome and weighting models. We first show that the combined estimator that uses (kernel) ridge regression for both outcome and weighting models is equivalent to a single, undersmoothed (kernel) ridge regression; this also holds when considering asymptotic rates. When the weighting model is instead lasso regression, we give closed-form expressions for special cases and demonstrate a ``double selection'' property. Finally, we generalize these results to linear estimands via the Riesz representer. Our framework ``opens the black box'' on these increasingly popular estimators and provides important insights into estimation choices for augmented balancing weights.

Robust Fitted-Q-Evaluation and Iteration under Sequentially Exogenous Unobserved Confounders

Offline reinforcement learning is important in domains such as medicine, economics, and e-commerce where online experimentation is costly, dangerous or unethical, and where the true model is unknown. However, most methods assume all covariates used in the behavior policy's action decisions are observed. This untestable assumption may be incorrect. We study robust policy evaluation and policy optimization in the presence of unobserved confounders. We assume the extent of possible unobserved confounding can be bounded by a sensitivity model, and that the unobserved confounders are sequentially exogenous. We propose and analyze an (orthogonalized) robust fitted-Q-iteration that uses closed-form solutions of the robust Bellman operator to derive a loss minimization problem for the robust Q function. Our algorithm enjoys the computational ease of fitted-Q-iteration and statistical improvements (reduced dependence on quantile estimation error) from orthogonalization. We provide sample complexity bounds, insights, and show effectiveness in simulations.

Model-Free and Model-Based Policy Evaluation when Causality is Uncertain

When decision-makers can directly intervene, policy evaluation algorithms give valid causal estimates. In off-policy evaluation (OPE), there may exist unobserved variables that both impact the dynamics and are used by the unknown behavior policy. These "confounders" will introduce spurious correlations and naive estimates for a new policy will be biased. We develop worst-case bounds to assess sensitivity to these unobserved confounders in finite horizons when confounders are drawn iid each period. We demonstrate that a model-based approach with robust MDPs gives sharper lower bounds by exploiting domain knowledge about the dynamics. Finally, we show that when unobserved confounders are persistent over time, OPE is far more difficult and existing techniques produce extremely conservative bounds.

Outcome Assumptions and Duality Theory for Balancing Weights

We study balancing weight estimators, which reweight outcomes from a source population to estimate missing outcomes in a target population. These estimators minimize the worst-case error by making an assumption about the outcome model. In this paper, we show that this outcome assumption has two immediate implications. First, we can replace the minimax optimization problem for balancing weights with a simple convex loss over the assumed outcome function class. Second, we can replace the commonly-made overlap assumption with a more appropriate quantitative measure, the minimum worst-case bias. Finally, we show conditions under which the weights remain robust when our assumptions on the outcomes are wrong.