Konrad P. Kording
Teresa
A Scalable, Causal, and Energy Efficient Framework for Neural Decoding with Spiking Neural Networks
Oct 23, 2025Abstract:Brain-computer interfaces (BCIs) promise to enable vital functions, such as speech and prosthetic control, for individuals with neuromotor impairments. Central to their success are neural decoders, models that map neural activity to intended behavior. Current learning-based decoding approaches fall into two classes: simple, causal models that lack generalization, or complex, non-causal models that generalize and scale offline but struggle in real-time settings. Both face a common challenge, their reliance on power-hungry artificial neural network backbones, which makes integration into real-world, resource-limited systems difficult. Spiking neural networks (SNNs) offer a promising alternative. Because they operate causally these models are suitable for real-time use, and their low energy demands make them ideal for battery-constrained environments. To this end, we introduce Spikachu: a scalable, causal, and energy-efficient neural decoding framework based on SNNs. Our approach processes binned spikes directly by projecting them into a shared latent space, where spiking modules, adapted to the timing of the input, extract relevant features; these latent representations are then integrated and decoded to generate behavioral predictions. We evaluate our approach on 113 recording sessions from 6 non-human primates, totaling 43 hours of recordings. Our method outperforms causal baselines when trained on single sessions using between 2.26 and 418.81 times less energy. Furthermore, we demonstrate that scaling up training to multiple sessions and subjects improves performance and enables few-shot transfer to unseen sessions, subjects, and tasks. Overall, Spikachu introduces a scalable, online-compatible neural decoding framework based on SNNs, whose performance is competitive relative to state-of-the-art models while consuming orders of magnitude less energy.
Grounding Intelligence in Movement
Jul 03, 2025
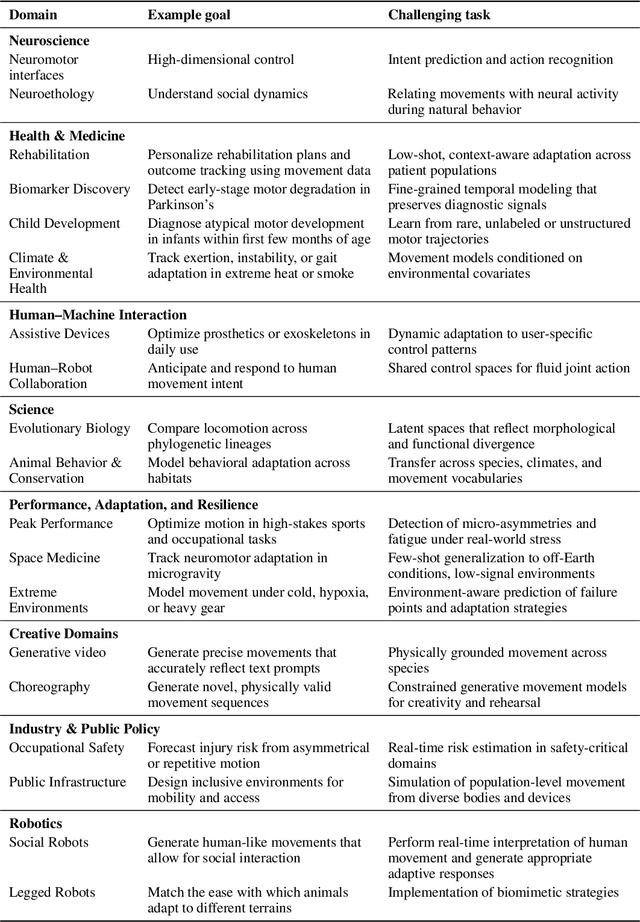
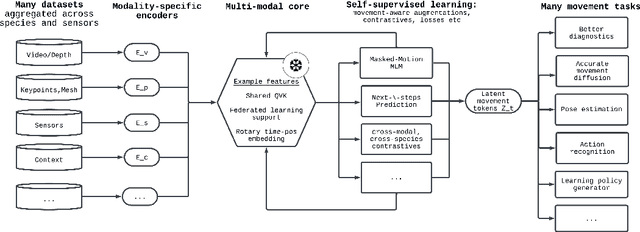
Abstract:Recent advances in machine learning have dramatically improved our ability to model language, vision, and other high-dimensional data, yet they continue to struggle with one of the most fundamental aspects of biological systems: movement. Across neuroscience, medicine, robotics, and ethology, movement is essential for interpreting behavior, predicting intent, and enabling interaction. Despite its core significance in our intelligence, movement is often treated as an afterthought rather than as a rich and structured modality in its own right. This reflects a deeper fragmentation in how movement data is collected and modeled, often constrained by task-specific goals and domain-specific assumptions. But movement is not domain-bound. It reflects shared physical constraints, conserved morphological structures, and purposeful dynamics that cut across species and settings. We argue that movement should be treated as a primary modeling target for AI. It is inherently structured and grounded in embodiment and physics. This structure, often allowing for compact, lower-dimensional representations (e.g., pose), makes it more interpretable and computationally tractable to model than raw, high-dimensional sensory inputs. Developing models that can learn from and generalize across diverse movement data will not only advance core capabilities in generative modeling and control, but also create a shared foundation for understanding behavior across biological and artificial systems. Movement is not just an outcome, it is a window into how intelligent systems engage with the world.
Who Does What in Deep Learning? Multidimensional Game-Theoretic Attribution of Function of Neural Units
Jun 24, 2025Abstract:Neural networks now generate text, images, and speech with billions of parameters, producing a need to know how each neural unit contributes to these high-dimensional outputs. Existing explainable-AI methods, such as SHAP, attribute importance to inputs, but cannot quantify the contributions of neural units across thousands of output pixels, tokens, or logits. Here we close that gap with Multiperturbation Shapley-value Analysis (MSA), a model-agnostic game-theoretic framework. By systematically lesioning combinations of units, MSA yields Shapley Modes, unit-wise contribution maps that share the exact dimensionality of the model's output. We apply MSA across scales, from multi-layer perceptrons to the 56-billion-parameter Mixtral-8x7B and Generative Adversarial Networks (GAN). The approach demonstrates how regularisation concentrates computation in a few hubs, exposes language-specific experts inside the LLM, and reveals an inverted pixel-generation hierarchy in GANs. Together, these results showcase MSA as a powerful approach for interpreting, editing, and compressing deep neural networks.
The Landscape of Causal Discovery Data: Grounding Causal Discovery in Real-World Applications
Dec 02, 2024

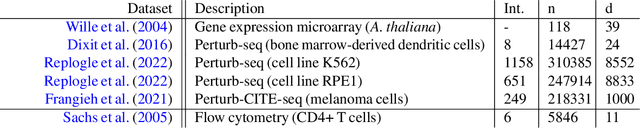

Abstract:Causal discovery aims to automatically uncover causal relationships from data, a capability with significant potential across many scientific disciplines. However, its real-world applications remain limited. Current methods often rely on unrealistic assumptions and are evaluated only on simple synthetic toy datasets, often with inadequate evaluation metrics. In this paper, we substantiate these claims by performing a systematic review of the recent causal discovery literature. We present applications in biology, neuroscience, and Earth sciences - fields where causal discovery holds promise for addressing key challenges. We highlight available simulated and real-world datasets from these domains and discuss common assumption violations that have spurred the development of new methods. Our goal is to encourage the community to adopt better evaluation practices by utilizing realistic datasets and more adequate metrics.
Empirical influence functions to understand the logic of fine-tuning
Jun 01, 2024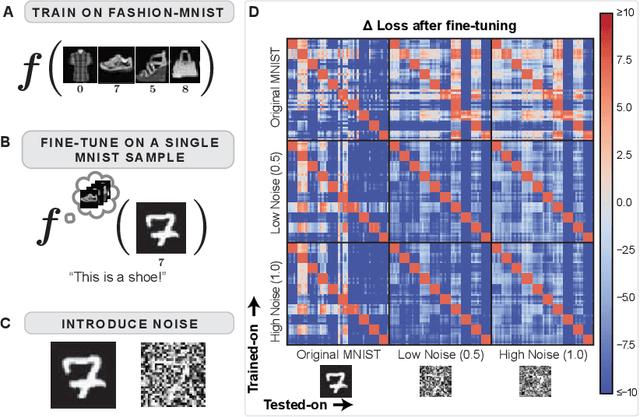
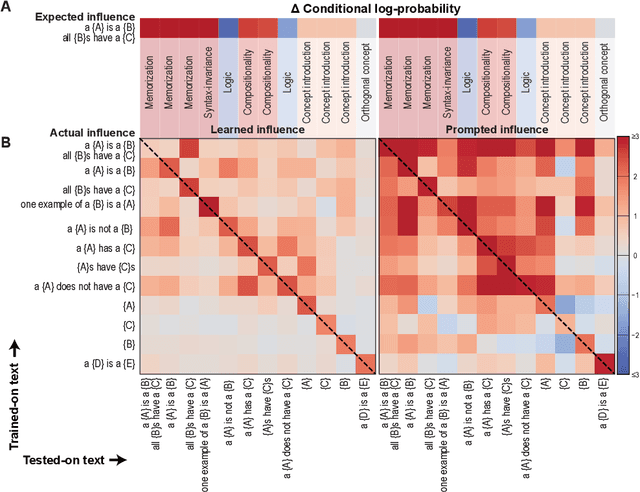
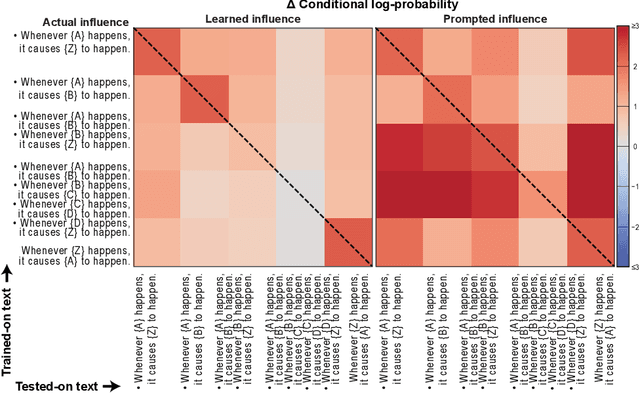
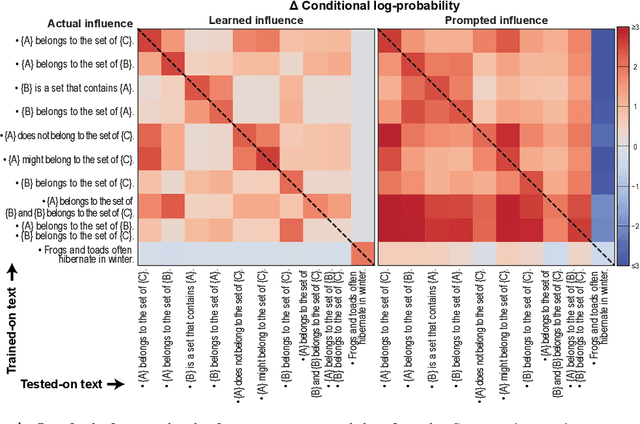
Abstract:Understanding the process of learning in neural networks is crucial for improving their performance and interpreting their behavior. This can be approximately understood by asking how a model's output is influenced when we fine-tune on a new training sample. There are desiderata for such influences, such as decreasing influence with semantic distance, sparseness, noise invariance, transitive causality, and logical consistency. Here we use the empirical influence measured using fine-tuning to demonstrate how individual training samples affect outputs. We show that these desiderata are violated for both for simple convolutional networks and for a modern LLM. We also illustrate how prompting can partially rescue this failure. Our paper presents an efficient and practical way of quantifying how well neural networks learn from fine-tuning stimuli. Our results suggest that popular models cannot generalize or perform logic in the way they appear to.
A large language model-assisted education tool to provide feedback on open-ended responses
Jul 25, 2023Abstract:Open-ended questions are a favored tool among instructors for assessing student understanding and encouraging critical exploration of course material. Providing feedback for such responses is a time-consuming task that can lead to overwhelmed instructors and decreased feedback quality. Many instructors resort to simpler question formats, like multiple-choice questions, which provide immediate feedback but at the expense of personalized and insightful comments. Here, we present a tool that uses large language models (LLMs), guided by instructor-defined criteria, to automate responses to open-ended questions. Our tool delivers rapid personalized feedback, enabling students to quickly test their knowledge and identify areas for improvement. We provide open-source reference implementations both as a web application and as a Jupyter Notebook widget that can be used with instructional coding or math notebooks. With instructor guidance, LLMs hold promise to enhance student learning outcomes and elevate instructional methodologies.
Neural Networks as Paths through the Space of Representations
Jun 22, 2022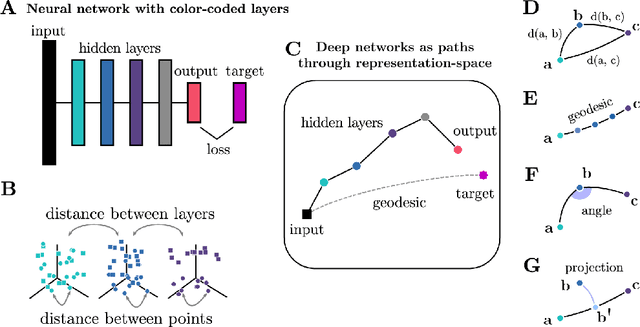
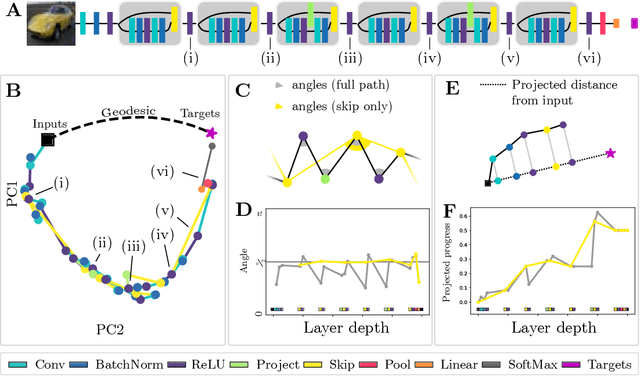
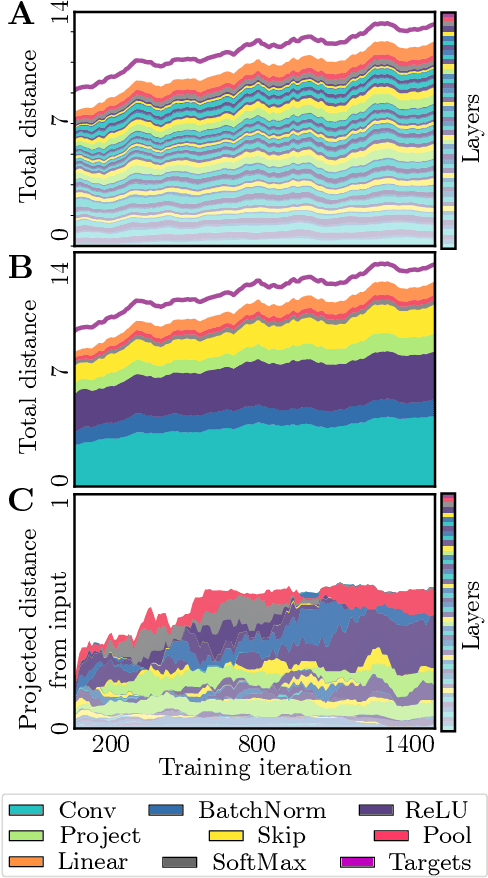
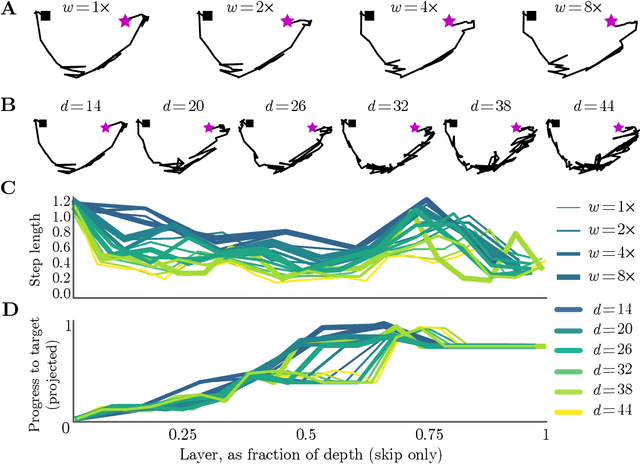
Abstract:Deep neural networks implement a sequence of layer-by-layer operations that are each relatively easy to understand, but the resulting overall computation is generally difficult to understand. We develop a simple idea for interpreting the layer-by-layer construction of useful representations: the role of each layer is to reformat information to reduce the "distance" to the target outputs. We formalize this intuitive idea of "distance" by leveraging recent work on metric representational similarity, and show how it leads to a rich space of geometric concepts. With this framework, the layer-wise computation implemented by a deep neural network can be viewed as a path in a high-dimensional representation space. We develop tools to characterize the geometry of these in terms of distances, angles, and geodesics. We then ask three sets of questions of residual networks trained on CIFAR-10: (1) how straight are paths, and how does each layer contribute towards the target? (2) how do these properties emerge over training? and (3) how similar are the paths taken by wider versus deeper networks? We conclude by sketching additional ways that this kind of representational geometry can be used to understand and interpret network training, or to prescriptively improve network architectures to suit a task.
Clustering units in neural networks: upstream vs downstream information
Mar 22, 2022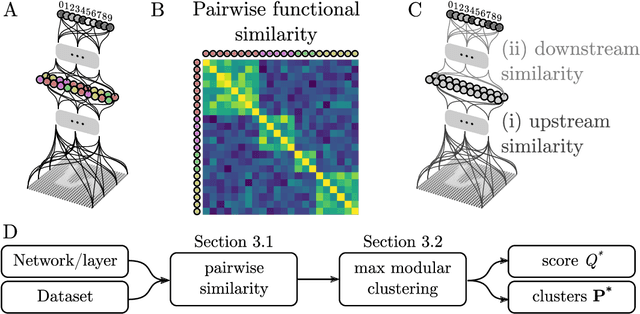
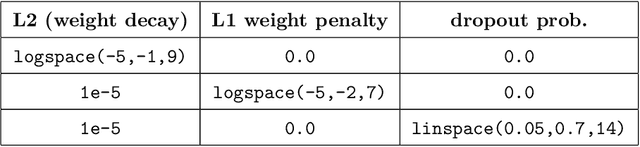
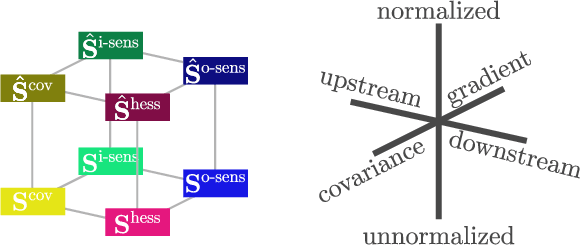
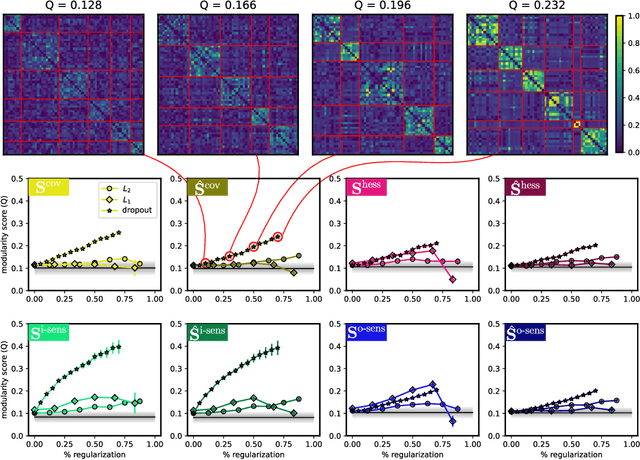
Abstract:It has been hypothesized that some form of "modular" structure in artificial neural networks should be useful for learning, compositionality, and generalization. However, defining and quantifying modularity remains an open problem. We cast the problem of detecting functional modules into the problem of detecting clusters of similar-functioning units. This begs the question of what makes two units functionally similar. For this, we consider two broad families of methods: those that define similarity based on how units respond to structured variations in inputs ("upstream"), and those based on how variations in hidden unit activations affect outputs ("downstream"). We conduct an empirical study quantifying modularity of hidden layer representations of simple feedforward, fully connected networks, across a range of hyperparameters. For each model, we quantify pairwise associations between hidden units in each layer using a variety of both upstream and downstream measures, then cluster them by maximizing their "modularity score" using established tools from network science. We find two surprising results: first, dropout dramatically increased modularity, while other forms of weight regularization had more modest effects. Second, although we observe that there is usually good agreement about clusters within both upstream methods and downstream methods, there is little agreement about the cluster assignments across these two families of methods. This has important implications for representation-learning, as it suggests that finding modular representations that reflect structure in inputs (e.g. disentanglement) may be a distinct goal from learning modular representations that reflect structure in outputs (e.g. compositionality).
Prospective Learning: Back to the Future
Jan 19, 2022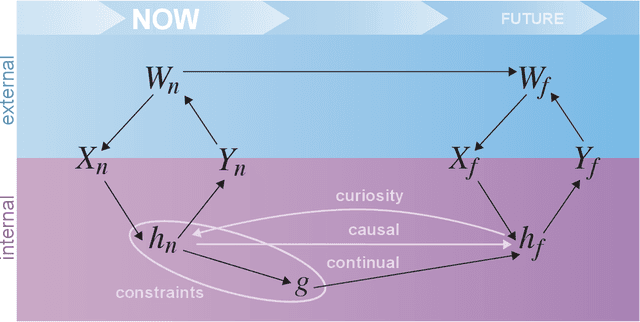

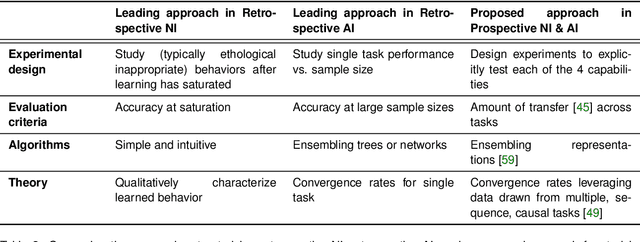
Abstract:Research on both natural intelligence (NI) and artificial intelligence (AI) generally assumes that the future resembles the past: intelligent agents or systems (what we call 'intelligence') observe and act on the world, then use this experience to act on future experiences of the same kind. We call this 'retrospective learning'. For example, an intelligence may see a set of pictures of objects, along with their names, and learn to name them. A retrospective learning intelligence would merely be able to name more pictures of the same objects. We argue that this is not what true intelligence is about. In many real world problems, both NIs and AIs will have to learn for an uncertain future. Both must update their internal models to be useful for future tasks, such as naming fundamentally new objects and using these objects effectively in a new context or to achieve previously unencountered goals. This ability to learn for the future we call 'prospective learning'. We articulate four relevant factors that jointly define prospective learning. Continual learning enables intelligences to remember those aspects of the past which it believes will be most useful in the future. Prospective constraints (including biases and priors) facilitate the intelligence finding general solutions that will be applicable to future problems. Curiosity motivates taking actions that inform future decision making, including in previously unmet situations. Causal estimation enables learning the structure of relations that guide choosing actions for specific outcomes, even when the specific action-outcome contingencies have never been observed before. We argue that a paradigm shift from retrospective to prospective learning will enable the communities that study intelligence to unite and overcome existing bottlenecks to more effectively explain, augment, and engineer intelligences.
Object Based Attention Through Internal Gating
Jun 08, 2021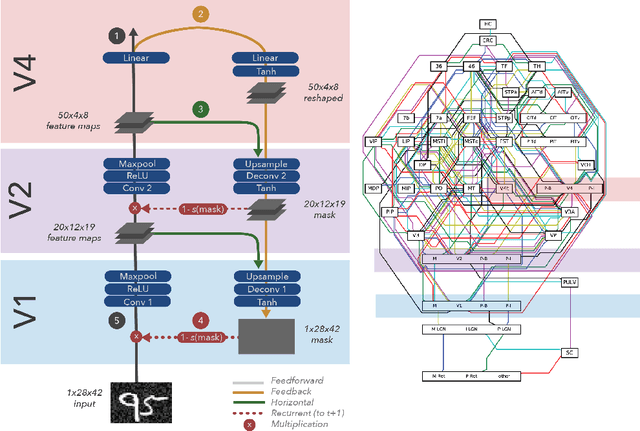
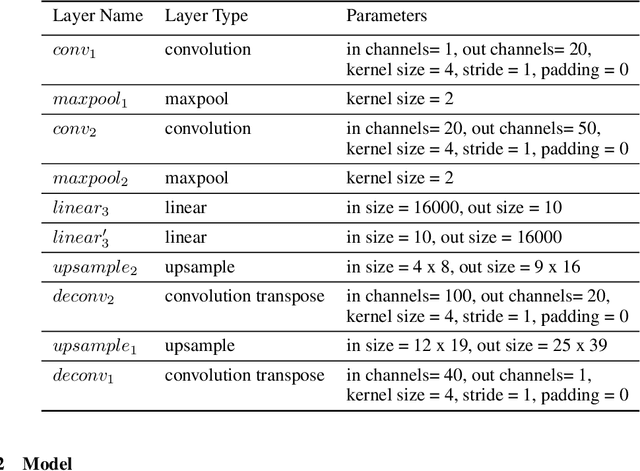
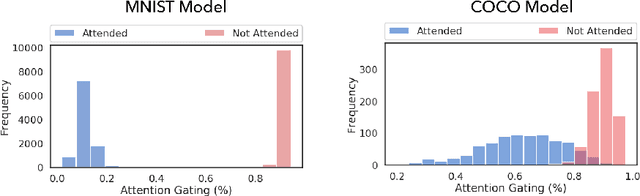

Abstract:Object-based attention is a key component of the visual system, relevant for perception, learning, and memory. Neurons tuned to features of attended objects tend to be more active than those associated with non-attended objects. There is a rich set of models of this phenomenon in computational neuroscience. However, there is currently a divide between models that successfully match physiological data but can only deal with extremely simple problems and models of attention used in computer vision. For example, attention in the brain is known to depend on top-down processing, whereas self-attention in deep learning does not. Here, we propose an artificial neural network model of object-based attention that captures the way in which attention is both top-down and recurrent. Our attention model works well both on simple test stimuli, such as those using images of handwritten digits, and on more complex stimuli, such as natural images drawn from the COCO dataset. We find that our model replicates a range of findings from neuroscience, including attention-invariant tuning, inhibition of return, and attention-mediated scaling of activity. Understanding object based attention is both computationally interesting and a key problem for computational neuroscience.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge