When Counterfactual Reasoning Fails: Chaos and Real-World Complexity

Counterfactual reasoning, a cornerstone of human cognition and decision-making, is often seen as the 'holy grail' of causal learning, with applications ranging from interpreting machine learning models to promoting algorithmic fairness. While counterfactual reasoning has been extensively studied in contexts where the underlying causal model is well-defined, real-world causal modeling is often hindered by model and parameter uncertainty, observational noise, and chaotic behavior. The reliability of counterfactual analysis in such settings remains largely unexplored. In this work, we investigate the limitations of counterfactual reasoning within the framework of Structural Causal Models. Specifically, we empirically investigate \emph{counterfactual sequence estimation} and highlight cases where it becomes increasingly unreliable. We find that realistic assumptions, such as low degrees of model uncertainty or chaotic dynamics, can result in counterintuitive outcomes, including dramatic deviations between predicted and true counterfactual trajectories. This work urges caution when applying counterfactual reasoning in settings characterized by chaos and uncertainty. Furthermore, it raises the question of whether certain systems may pose fundamental limitations on the ability to answer counterfactual questions about their behavior.

Internal Incoherency Scores for Constraint-based Causal Discovery Algorithms

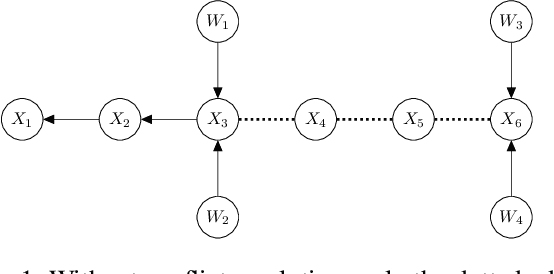
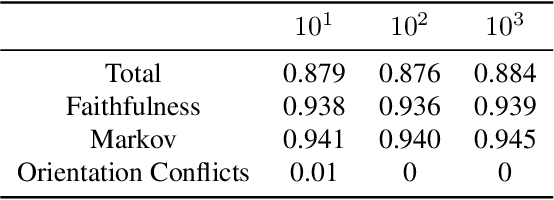
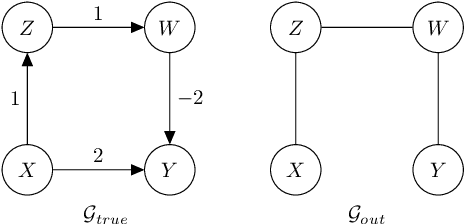
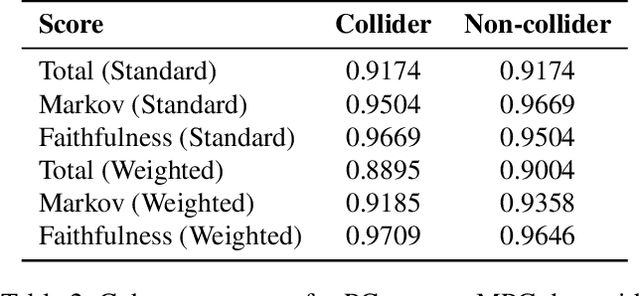
Causal discovery aims to infer causal graphs from observational or experimental data. Methods such as the popular PC algorithm are based on conditional independence testing and utilize enabling assumptions, such as the faithfulness assumption, for their inferences. In practice, these assumptions, as well as the functional assumptions inherited from the chosen conditional independence test, are typically taken as a given and not further tested for their validity on the data. In this work, we propose internal coherency scores that allow testing for assumption violations and finite sample errors, whenever detectable without requiring ground truth or further statistical tests. We provide a complete classification of erroneous results, including a distinction between detectable and undetectable errors, and prove that the detectable erroneous results can be measured by our scores. We illustrate our coherency scores on the PC algorithm with simulated and real-world datasets, and envision that testing for internal coherency can become a standard tool in applying constraint-based methods, much like a suite of tests is used to validate the assumptions of classical regression analysis.

The Landscape of Causal Discovery Data: Grounding Causal Discovery in Real-World Applications

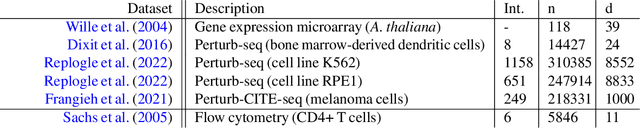
Causal discovery aims to automatically uncover causal relationships from data, a capability with significant potential across many scientific disciplines. However, its real-world applications remain limited. Current methods often rely on unrealistic assumptions and are evaluated only on simple synthetic toy datasets, often with inadequate evaluation metrics. In this paper, we substantiate these claims by performing a systematic review of the recent causal discovery literature. We present applications in biology, neuroscience, and Earth sciences - fields where causal discovery holds promise for addressing key challenges. We highlight available simulated and real-world datasets from these domains and discuss common assumption violations that have spurred the development of new methods. Our goal is to encourage the community to adopt better evaluation practices by utilizing realistic datasets and more adequate metrics.

Sortability of Time Series Data

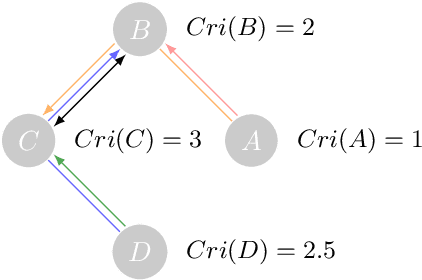
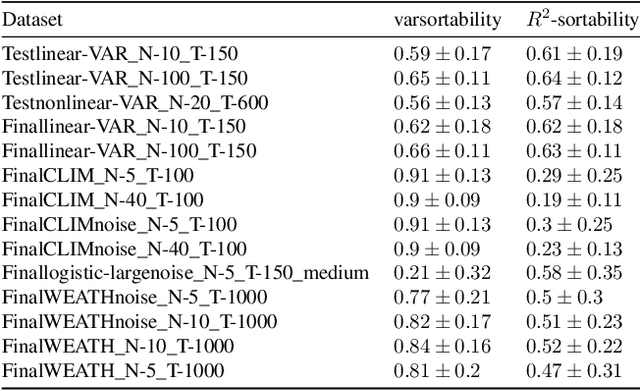
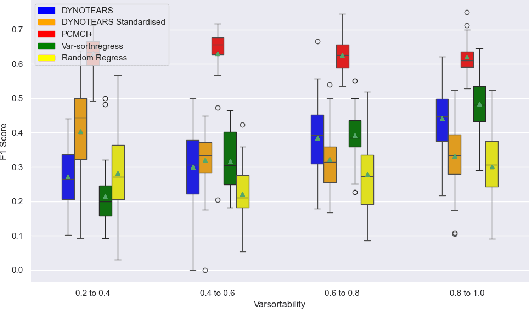
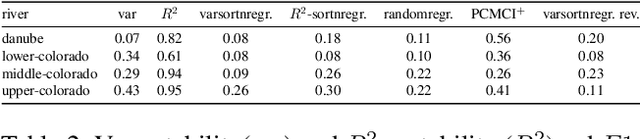
Evaluating the performance of causal discovery algorithms that aim to find causal relationships between time-dependent processes remains a challenging topic. In this paper, we show that certain characteristics of datasets, such as varsortability (Reisach et al. 2021) and $R^2$-sortability (Reisach et al. 2023), also occur in datasets for autocorrelated stationary time series. We illustrate this empirically using four types of data: simulated data based on SVAR models and Erd\H{o}s-R\'enyi graphs, the data used in the 2019 causality-for-climate challenge (Runge et al. 2019), real-world river stream datasets, and real-world data generated by the Causal Chamber of (Gamella et al. 2024). To do this, we adapt var- and $R^2$-sortability to time series data. We also investigate the extent to which the performance of score-based causal discovery methods goes hand in hand with high sortability. Arguably, our most surprising finding is that the investigated real-world datasets exhibit high varsortability and low $R^2$-sortability indicating that scales may carry a significant amount of causal information.

Metrics on Markov Equivalence Classes for Evaluating Causal Discovery Algorithms

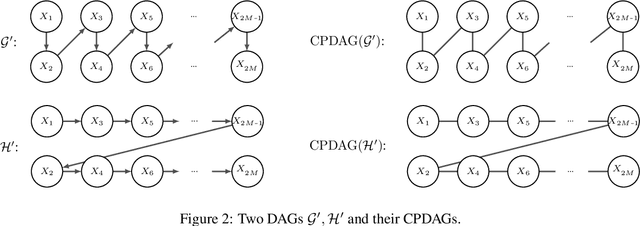
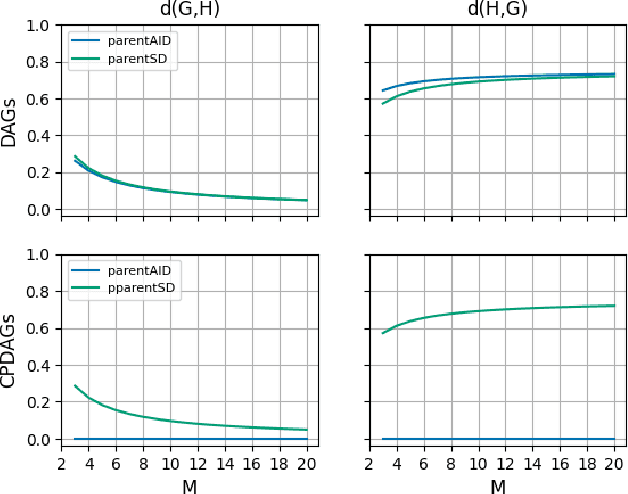
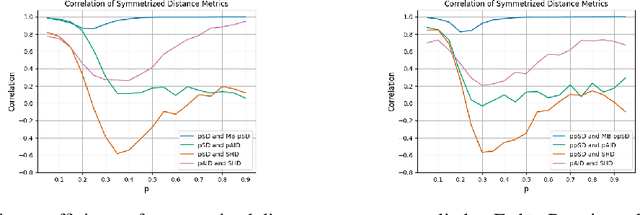
Many state-of-the-art causal discovery methods aim to generate an output graph that encodes the graphical separation and connection statements of the causal graph that underlies the data-generating process. In this work, we argue that an evaluation of a causal discovery method against synthetic data should include an analysis of how well this explicit goal is achieved by measuring how closely the separations/connections of the method's output align with those of the ground truth. We show that established evaluation measures do not accurately capture the difference in separations/connections of two causal graphs, and we introduce three new measures of distance called s/c-distance, Markov distance and Faithfulness distance that address this shortcoming. We complement our theoretical analysis with toy examples, empirical experiments and pseudocode.

Invariance & Causal Representation Learning: Prospects and Limitations

In causal models, a given mechanism is assumed to be invariant to changes of other mechanisms. While this principle has been utilized for inference in settings where the causal variables are observed, theoretical insights when the variables of interest are latent are largely missing. We assay the connection between invariance and causal representation learning by establishing impossibility results which show that invariance alone is insufficient to identify latent causal variables. Together with practical considerations, we use these theoretical findings to highlight the need for additional constraints in order to identify representations by exploiting invariance.

Identifying Linearly-Mixed Causal Representations from Multi-Node Interventions

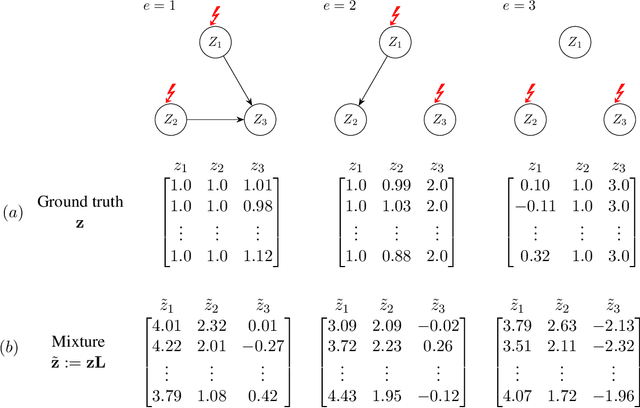
The task of inferring high-level causal variables from low-level observations, commonly referred to as causal representation learning, is fundamentally underconstrained. As such, recent works to address this problem focus on various assumptions that lead to identifiability of the underlying latent causal variables. A large corpus of these preceding approaches consider multi-environment data collected under different interventions on the causal model. What is common to virtually all of these works is the restrictive assumption that in each environment, only a single variable is intervened on. In this work, we relax this assumption and provide the first identifiability result for causal representation learning that allows for multiple variables to be targeted by an intervention within one environment. Our approach hinges on a general assumption on the coverage and diversity of interventions across environments, which also includes the shared assumption of single-node interventions of previous works. The main idea behind our approach is to exploit the trace that interventions leave on the variance of the ground truth causal variables and regularizing for a specific notion of sparsity with respect to this trace. In addition to and inspired by our theoretical contributions, we present a practical algorithm to learn causal representations from multi-node interventional data and provide empirical evidence that validates our identifiability results.

Projecting infinite time series graphs to finite marginal graphs using number theory

In recent years, a growing number of method and application works have adapted and applied the causal-graphical-model framework to time series data. Many of these works employ time-resolved causal graphs that extend infinitely into the past and future and whose edges are repetitive in time, thereby reflecting the assumption of stationary causal relationships. However, most results and algorithms from the causal-graphical-model framework are not designed for infinite graphs. In this work, we develop a method for projecting infinite time series graphs with repetitive edges to marginal graphical models on a finite time window. These finite marginal graphs provide the answers to $m$-separation queries with respect to the infinite graph, a task that was previously unresolved. Moreover, we argue that these marginal graphs are useful for causal discovery and causal effect estimation in time series, effectively enabling to apply results developed for finite graphs to the infinite graphs. The projection procedure relies on finding common ancestors in the to-be-projected graph and is, by itself, not new. However, the projection procedure has not yet been algorithmically implemented for time series graphs since in these infinite graphs there can be infinite sets of paths that might give rise to common ancestors. We solve the search over these possibly infinite sets of paths by an intriguing combination of path-finding techniques for finite directed graphs and solution theory for linear Diophantine equations. By providing an algorithm that carries out the projection, our paper makes an important step towards a theoretically-grounded and method-agnostic generalization of a range of causal inference methods and results to time series.