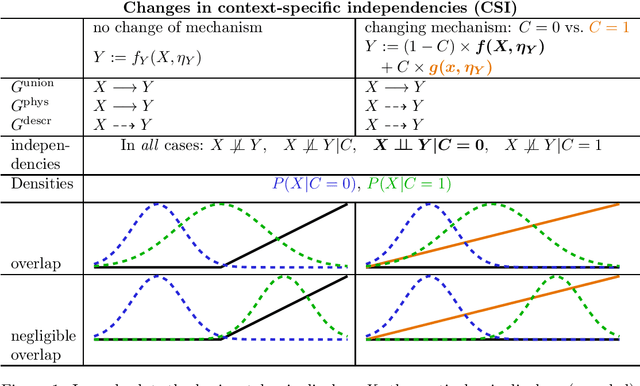
Causal Modeling in Multi-Context Systems: Distinguishing Multiple Context-Specific Causal Graphs which Account for Observational Support

Causal structure learning with data from multiple contexts carries both opportunities and challenges. Opportunities arise from considering shared and context-specific causal graphs enabling to generalize and transfer causal knowledge across contexts. However, a challenge that is currently understudied in the literature is the impact of differing observational support between contexts on the identifiability of causal graphs. Here we study in detail recently introduced [6] causal graph objects that capture both causal mechanisms and data support, allowing for the analysis of a larger class of context-specific changes, characterizing distribution shifts more precisely. We thereby extend results on the identifiability of context-specific causal structures and propose a framework to model context-specific independence (CSI) within structural causal models (SCMs) in a refined way that allows to explore scenarios where these graph objects differ. We demonstrate how this framework can help explaining phenomena like anomalies or extreme events, where causal mechanisms change or appear to change under different conditions. Our results contribute to the theoretical foundations for understanding causal relations in multi-context systems, with implications for generalization, transfer learning, and anomaly detection. Future work may extend this approach to more complex data types, such as time-series.

Non-parametric Conditional Independence Testing for Mixed Continuous-Categorical Variables: A Novel Method and Numerical Evaluation

Conditional independence testing (CIT) is a common task in machine learning, e.g., for variable selection, and a main component of constraint-based causal discovery. While most current CIT approaches assume that all variables are numerical or all variables are categorical, many real-world applications involve mixed-type datasets that include numerical and categorical variables. Non-parametric CIT can be conducted using conditional mutual information (CMI) estimators combined with a local permutation scheme. Recently, two novel CMI estimators for mixed-type datasets based on k-nearest-neighbors (k-NN) have been proposed. As with any k-NN method, these estimators rely on the definition of a distance metric. One approach computes distances by a one-hot encoding of the categorical variables, essentially treating categorical variables as discrete-numerical, while the other expresses CMI by entropy terms where the categorical variables appear as conditions only. In this work, we study these estimators and propose a variation of the former approach that does not treat categorical variables as numeric. Our numerical experiments show that our variant detects dependencies more robustly across different data distributions and preprocessing types.

Projecting infinite time series graphs to finite marginal graphs using number theory

In recent years, a growing number of method and application works have adapted and applied the causal-graphical-model framework to time series data. Many of these works employ time-resolved causal graphs that extend infinitely into the past and future and whose edges are repetitive in time, thereby reflecting the assumption of stationary causal relationships. However, most results and algorithms from the causal-graphical-model framework are not designed for infinite graphs. In this work, we develop a method for projecting infinite time series graphs with repetitive edges to marginal graphical models on a finite time window. These finite marginal graphs provide the answers to $m$-separation queries with respect to the infinite graph, a task that was previously unresolved. Moreover, we argue that these marginal graphs are useful for causal discovery and causal effect estimation in time series, effectively enabling to apply results developed for finite graphs to the infinite graphs. The projection procedure relies on finding common ancestors in the to-be-projected graph and is, by itself, not new. However, the projection procedure has not yet been algorithmically implemented for time series graphs since in these infinite graphs there can be infinite sets of paths that might give rise to common ancestors. We solve the search over these possibly infinite sets of paths by an intriguing combination of path-finding techniques for finite directed graphs and solution theory for linear Diophantine equations. By providing an algorithm that carries out the projection, our paper makes an important step towards a theoretically-grounded and method-agnostic generalization of a range of causal inference methods and results to time series.

Bootstrap aggregation and confidence measures to improve time series causal discovery

Causal discovery methods have demonstrated the ability to identify the time series graphs representing the causal temporal dependency structure of dynamical systems. However, they do not include a measure of the confidence of the estimated links. Here, we introduce a novel bootstrap aggregation (bagging) and confidence measure method that is combined with time series causal discovery. This new method allows measuring confidence for the links of the time series graphs calculated by causal discovery methods. This is done by bootstrapping the original times series data set while preserving temporal dependencies. Next to confidence measures, aggregating the bootstrapped graphs by majority voting yields a final aggregated output graph. In this work, we combine our approach with the state-of-the-art conditional-independence-based algorithm PCMCI+. With extensive numerical experiments we empirically demonstrate that, in addition to providing confidence measures for links, Bagged-PCMCI+ improves the precision and recall of its base algorithm PCMCI+. Specifically, Bagged-PCMCI+ has a higher detection power regarding adjacencies and a higher precision in orienting contemporaneous edges while at the same time showing a lower rate of false positives. These performance improvements are especially pronounced in the more challenging settings (short time sample size, large number of variables, high autocorrelation). Our bootstrap approach can also be combined with other time series causal discovery algorithms and can be of considerable use in many real-world applications, especially when confidence measures for the links are desired.

Discovering Causal Relations and Equations from Data

Physics is a field of science that has traditionally used the scientific method to answer questions about why natural phenomena occur and to make testable models that explain the phenomena. Discovering equations, laws and principles that are invariant, robust and causal explanations of the world has been fundamental in physical sciences throughout the centuries. Discoveries emerge from observing the world and, when possible, performing interventional studies in the system under study. With the advent of big data and the use of data-driven methods, causal and equation discovery fields have grown and made progress in computer science, physics, statistics, philosophy, and many applied fields. All these domains are intertwined and can be used to discover causal relations, physical laws, and equations from observational data. This paper reviews the concepts, methods, and relevant works on causal and equation discovery in the broad field of Physics and outlines the most important challenges and promising future lines of research. We also provide a taxonomy for observational causal and equation discovery, point out connections, and showcase a complete set of case studies in Earth and climate sciences, fluid dynamics and mechanics, and the neurosciences. This review demonstrates that discovering fundamental laws and causal relations by observing natural phenomena is being revolutionised with the efficient exploitation of observational data, modern machine learning algorithms and the interaction with domain knowledge. Exciting times are ahead with many challenges and opportunities to improve our understanding of complex systems.

Selecting Robust Features for Machine Learning Applications using Multidata Causal Discovery

Robust feature selection is vital for creating reliable and interpretable Machine Learning (ML) models. When designing statistical prediction models in cases where domain knowledge is limited and underlying interactions are unknown, choosing the optimal set of features is often difficult. To mitigate this issue, we introduce a Multidata (M) causal feature selection approach that simultaneously processes an ensemble of time series datasets and produces a single set of causal drivers. This approach uses the causal discovery algorithms PC1 or PCMCI that are implemented in the Tigramite Python package. These algorithms utilize conditional independence tests to infer parts of the causal graph. Our causal feature selection approach filters out causally-spurious links before passing the remaining causal features as inputs to ML models (Multiple linear regression, Random Forest) that predict the targets. We apply our framework to the statistical intensity prediction of Western Pacific Tropical Cyclones (TC), for which it is often difficult to accurately choose drivers and their dimensionality reduction (time lags, vertical levels, and area-averaging). Using more stringent significance thresholds in the conditional independence tests helps eliminate spurious causal relationships, thus helping the ML model generalize better to unseen TC cases. M-PC1 with a reduced number of features outperforms M-PCMCI, non-causal ML, and other feature selection methods (lagged correlation, random), even slightly outperforming feature selection based on eXplainable Artificial Intelligence. The optimal causal drivers obtained from our causal feature selection help improve our understanding of underlying relationships and suggest new potential drivers of TC intensification.

Characterization of causal ancestral graphs for time series with latent confounders

Generalizing directed maximal ancestral graphs, we introduce a class of graphical models for representing time lag specific causal relationships and independencies among finitely many regularly sampled and regularly subsampled time steps of multivariate time series with unobserved variables. We completely characterize these graphs and show that they entail constraints beyond those that have previously been considered in the literature. This allows for stronger causal inferences without having imposed additional assumptions. In generalization of directed partial ancestral graphs we further introduce a graphical representation of Markov equivalence classes of the novel type of graphs and show that these are more informative than what current state-of-the-art causal discovery algorithms learn. We also analyze the additional information gained by increasing the number of observed time steps.

High-recall causal discovery for autocorrelated time series with latent confounders

We present a new method for linear and nonlinear, lagged and contemporaneous constraint-based causal discovery from observational time series in the presence of latent confounders. We show that existing causal discovery methods such as FCI and variants suffer from low recall in the autocorrelated time series case and identify low effect size of conditional independence tests as the main reason. Information-theoretical arguments show that effect size can often be increased if causal parents are included in the conditioning sets. To identify parents early on, we suggest an iterative procedure that utilizes novel orientation rules to determine ancestral relationships already during the edge removal phase. We prove that the method is order-independent, and sound and complete in the oracle case. Extensive simulation studies for different numbers of variables, time lags, sample sizes, and further cases demonstrate that our method indeed achieves much higher recall than existing methods while keeping false positives at the desired level. This performance gain grows with stronger autocorrelation. Our method also covers causal discovery for non-time series data as a special case. We provide Python code for all methods involved in the simulation studies.