Towards Infinitely Long Neural Simulations: Self-Refining Neural Surrogate Models for Dynamical Systems

Recent advances in autoregressive neural surrogate models have enabled orders-of-magnitude speedups in simulating dynamical systems. However, autoregressive models are generally prone to distribution drift: compounding errors in autoregressive rollouts that severely degrade generation quality over long time horizons. Existing work attempts to address this issue by implicitly leveraging the inherent trade-off between short-time accuracy and long-time consistency through hyperparameter tuning. In this work, we introduce a unifying mathematical framework that makes this tradeoff explicit, formalizing and generalizing hyperparameter-based strategies in existing approaches. Within this framework, we propose a robust, hyperparameter-free model implemented as a conditional diffusion model that balances short-time fidelity with long-time consistency by construction. Our model, Self-refining Neural Surrogate model (SNS), can be implemented as a standalone model that refines its own autoregressive outputs or as a complementary model to existing neural surrogates to ensure long-time consistency. We also demonstrate the numerical feasibility of SNS through high-fidelity simulations of complex dynamical systems over arbitrarily long time horizons.

FloeNet: A mass-conserving global sea ice emulator that generalizes across climates

We introduce FloeNet, a machine-learning emulator trained on the Geophysical Fluid Dynamics Laboratory global sea ice model, SIS2. FloeNet is a mass-conserving model, emulating 6-hour mass and area budget tendencies related to sea ice and snow-on-sea-ice growth, melt, and advection. We train FloeNet using simulated data from a reanalysis-forced ice-ocean simulation and test its ability to generalize to pre-industrial control and 1% CO2 climates. FloeNet outperforms a non-conservative model at reproducing sea ice and snow-on-sea-ice mean state, trends, and inter-annual variability, with volume anomaly correlations above 0.96 in the Antarctic and 0.76 in the Arctic, across all forcings. FloeNet also produces the correct thermodynamic vs dynamic response to forcing, enabling physical interpretability of emulator output. Finally, we show that FloeNet outputs high-fidelity coupling-related variables, including ice-surface skin temperature, ice-to-ocean salt flux, and melting energy fluxes. We hypothesize that FloeNet will improve polar climate processes within existing atmosphere and ocean emulators.

Causally constrained reduced-order neural models of complex turbulent dynamical systems

We introduce a flexible framework based on response theory and score matching to suppress spurious, noncausal dependencies in reduced-order neural emulators of turbulent systems, focusing on climate dynamics as a proof-of-concept. We showcase the approach using the stochastic Charney-DeVore model as a relevant prototype for low-frequency atmospheric variability. We show that the resulting causal constraints enhance neural emulators' ability to respond to both weak and strong external forcings, despite being trained exclusively on unforced data. The approach is broadly applicable to modeling complex turbulent dynamical systems in reduced spaces and can be readily integrated into general neural network architectures.

Accelerating scientific discovery with the common task framework

Machine learning (ML) and artificial intelligence (AI) algorithms are transforming and empowering the characterization and control of dynamic systems in the engineering, physical, and biological sciences. These emerging modeling paradigms require comparative metrics to evaluate a diverse set of scientific objectives, including forecasting, state reconstruction, generalization, and control, while also considering limited data scenarios and noisy measurements. We introduce a common task framework (CTF) for science and engineering, which features a growing collection of challenge data sets with a diverse set of practical and common objectives. The CTF is a critically enabling technology that has contributed to the rapid advance of ML/AI algorithms in traditional applications such as speech recognition, language processing, and computer vision. There is a critical need for the objective metrics of a CTF to compare the diverse algorithms being rapidly developed and deployed in practice today across science and engineering.

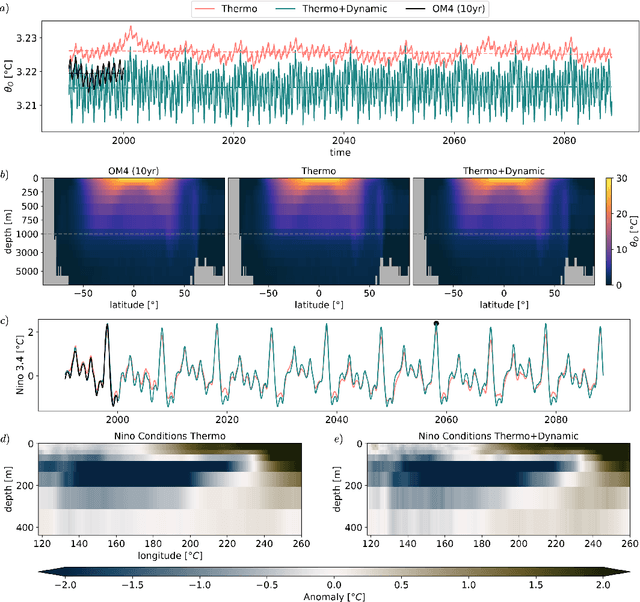
SamudrACE: Fast and Accurate Coupled Climate Modeling with 3D Ocean and Atmosphere Emulators

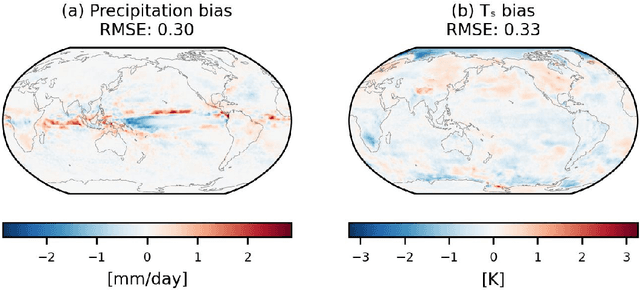
Traditional numerical global climate models simulate the full Earth system by exchanging boundary conditions between separate simulators of the atmosphere, ocean, sea ice, land surface, and other geophysical processes. This paradigm allows for distributed development of individual components within a common framework, unified by a coupler that handles translation between realms via spatial or temporal alignment and flux exchange. Following a similar approach adapted for machine learning-based emulators, we present SamudrACE: a coupled global climate model emulator which produces centuries-long simulations at 1-degree horizontal, 6-hourly atmospheric, and 5-daily oceanic resolution, with 145 2D fields spanning 8 atmospheric and 19 oceanic vertical levels, plus sea ice, surface, and top-of-atmosphere variables. SamudrACE is highly stable and has low climate biases comparable to those of its components with prescribed boundary forcing, with realistic variability in coupled climate phenomena such as ENSO that is not possible to simulate in uncoupled mode.

Fourier analysis of the physics of transfer learning for data-driven subgrid-scale models of ocean turbulence

Transfer learning (TL) is a powerful tool for enhancing the performance of neural networks (NNs) in applications such as weather and climate prediction and turbulence modeling. TL enables models to generalize to out-of-distribution data with minimal training data from the new system. In this study, we employ a 9-layer convolutional NN to predict the subgrid forcing in a two-layer ocean quasi-geostrophic system and examine which metrics best describe its performance and generalizability to unseen dynamical regimes. Fourier analysis of the NN kernels reveals that they learn low-pass, Gabor, and high-pass filters, regardless of whether the training data are isotropic or anisotropic. By analyzing the activation spectra, we identify why NNs fail to generalize without TL and how TL can overcome these limitations: the learned weights and biases from one dataset underestimate the out-of-distribution sample spectra as they pass through the network, leading to an underestimation of output spectra. By re-training only one layer with data from the target system, this underestimation is corrected, enabling the NN to produce predictions that match the target spectra. These findings are broadly applicable to data-driven parameterization of dynamical systems.

Thermalizer: Stable autoregressive neural emulation of spatiotemporal chaos

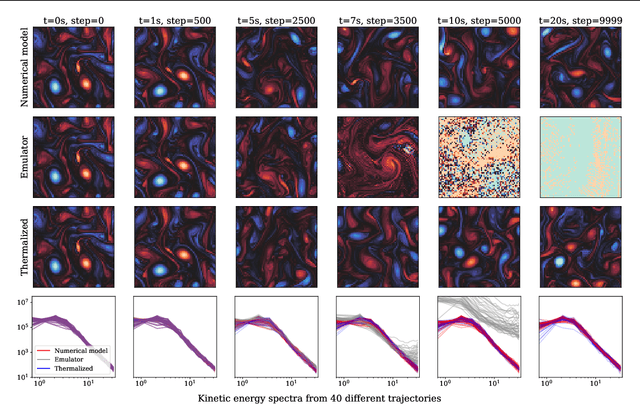
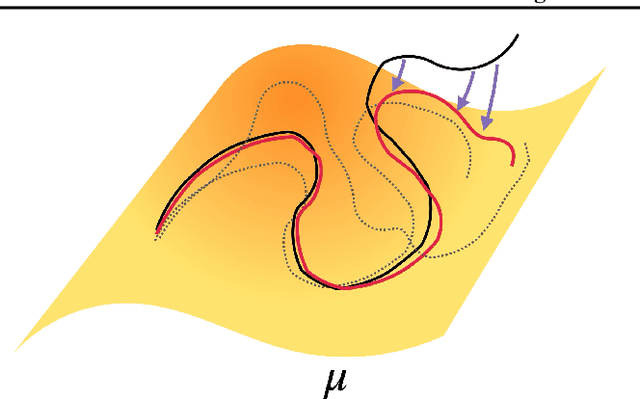
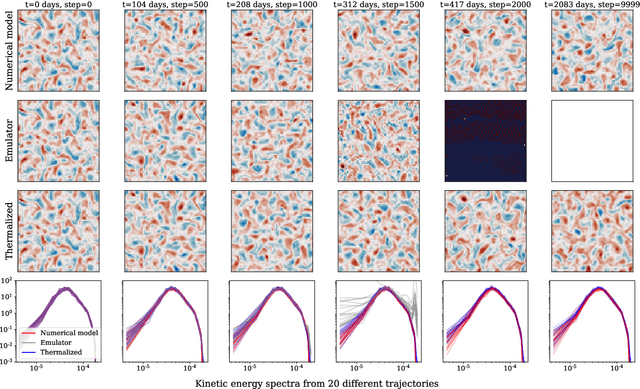
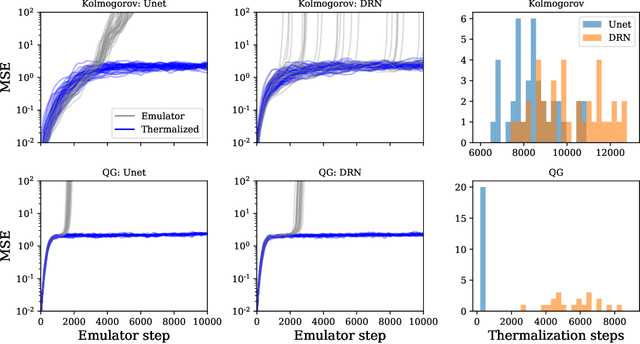
Autoregressive surrogate models (or \textit{emulators}) of spatiotemporal systems provide an avenue for fast, approximate predictions, with broad applications across science and engineering. At inference time, however, these models are generally unable to provide predictions over long time rollouts due to accumulation of errors leading to diverging trajectories. In essence, emulators operate out of distribution, and controlling the online distribution quickly becomes intractable in large-scale settings. To address this fundamental issue, and focusing on time-stationary systems admitting an invariant measure, we leverage diffusion models to obtain an implicit estimator of the score of this invariant measure. We show that this model of the score function can be used to stabilize autoregressive emulator rollouts by applying on-the-fly denoising during inference, a process we call \textit{thermalization}. Thermalizing an emulator rollout is shown to extend the time horizon of stable predictions by an order of magnitude in complex systems exhibiting turbulent and chaotic behavior, opening up a novel application of diffusion models in the context of neural emulation.

Data-Driven Probabilistic Air-Sea Flux Parameterization

Accurately quantifying air-sea fluxes is important for understanding air-sea interactions and improving coupled weather and climate systems. This study introduces a probabilistic framework to represent the highly variable nature of air-sea fluxes, which is missing in deterministic bulk algorithms. Assuming Gaussian distributions conditioned on the input variables, we use artificial neural networks and eddy-covariance measurement data to estimate the mean and variance by minimizing negative log-likelihood loss. The trained neural networks provide alternative mean flux estimates to existing bulk algorithms, and quantify the uncertainty around the mean estimates. Stochastic parameterization of air-sea turbulent fluxes can be constructed by sampling from the predicted distributions. Tests in a single-column forced upper-ocean model suggest that changes in flux algorithms influence sea surface temperature and mixed layer depth seasonally. The ensemble spread in stochastic runs is most pronounced during spring restratification.

Samudra: An AI Global Ocean Emulator for Climate

AI emulators for forecasting have emerged as powerful tools that can outperform conventional numerical predictions. The next frontier is to build emulators for long-term climate projections with robust skill across a wide range of spatiotemporal scales, a particularly important goal for the ocean. Our work builds a skillful global emulator of the ocean component of a state-of-the-art climate model. We emulate key ocean variables, sea surface height, horizontal velocities, temperature, and salinity, across their full depth. We use a modified ConvNeXt UNet architecture trained on multidepth levels of ocean data. We show that the ocean emulator - Samudra - which exhibits no drift relative to the truth, can reproduce the depth structure of ocean variables and their interannual variability. Samudra is stable for centuries and 150 times faster than the original ocean model. Samudra struggles to capture the correct magnitude of the forcing trends and simultaneously remains stable, requiring further work.

A Monte Carlo Framework for Calibrated Uncertainty Estimation in Sequence Prediction

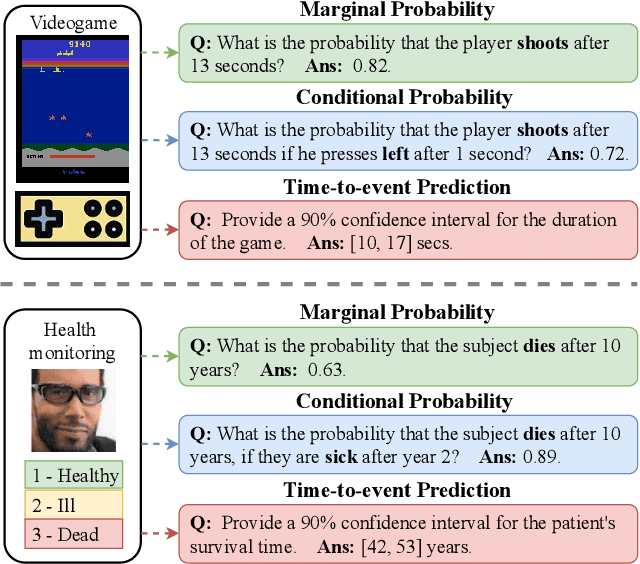
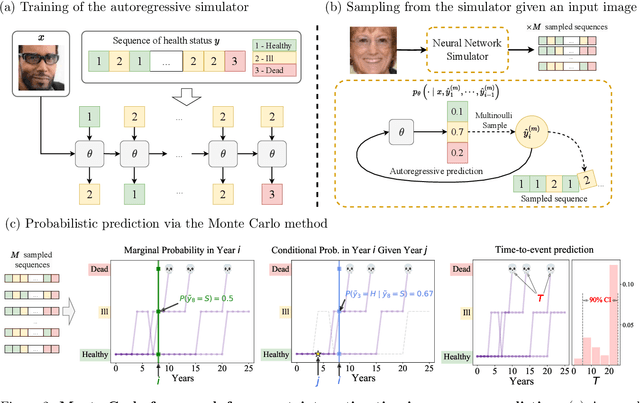
Probabilistic prediction of sequences from images and other high-dimensional data is a key challenge, particularly in risk-sensitive applications. In these settings, it is often desirable to quantify the uncertainty associated with the prediction (instead of just determining the most likely sequence, as in language modeling). In this paper, we propose a Monte Carlo framework to estimate probabilities and confidence intervals associated with the distribution of a discrete sequence. Our framework uses a Monte Carlo simulator, implemented as an autoregressively trained neural network, to sample sequences conditioned on an image input. We then use these samples to estimate the probabilities and confidence intervals. Experiments on synthetic and real data show that the framework produces accurate discriminative predictions, but can suffer from miscalibration. In order to address this shortcoming, we propose a time-dependent regularization method, which is shown to produce calibrated predictions.