Using Time Structure to Estimate Causal Effects

There exist several approaches for estimating causal effects in time series when latent confounding is present. Many of these approaches rely on additional auxiliary observed variables or time series such as instruments, negative controls or time series that satisfy the front- or backdoor criterion in certain graphs. In this paper, we present a novel approach for estimating direct (and via Wright's path rule total) causal effects in a time series setup which does not rely on additional auxiliary observed variables or time series. This approach assumes that the underlying time series is a Structural Vector Autoregressive (SVAR) process and estimates direct causal effects by solving certain linear equation systems made up of different covariances and model parameters. We state sufficient graphical criteria in terms of the so-called full time graph under which these linear equations systems are uniquely solvable and under which their solutions contain the to-be-identified direct causal effects as components. We also state sufficient lag-based criteria under which the previously mentioned graphical conditions are satisfied and, thus, under which direct causal effects are identifiable. Several numerical experiments underline the correctness and applicability of our results.

Sanity Checking Causal Representation Learning on a Simple Real-World System

We evaluate methods for causal representation learning (CRL) on a simple, real-world system where these methods are expected to work. The system consists of a controlled optical experiment specifically built for this purpose, which satisfies the core assumptions of CRL and where the underlying causal factors (the inputs to the experiment) are known, providing a ground truth. We select methods representative of different approaches to CRL and find that they all fail to recover the underlying causal factors. To understand the failure modes of the evaluated algorithms, we perform an ablation on the data by substituting the real data-generating process with a simpler synthetic equivalent. The results reveal a reproducibility problem, as most methods already fail on this synthetic ablation despite its simple data-generating process. Additionally, we observe that common assumptions on the mixing function are crucial for the performance of some of the methods but do not hold in the real data. Our efforts highlight the contrast between the theoretical promise of the state of the art and the challenges in its application. We hope the benchmark serves as a simple, real-world sanity check to further develop and validate methodology, bridging the gap towards CRL methods that work in practice. We make all code and datasets publicly available at github.com/simonbing/CRLSanityCheck

Internal Incoherency Scores for Constraint-based Causal Discovery Algorithms

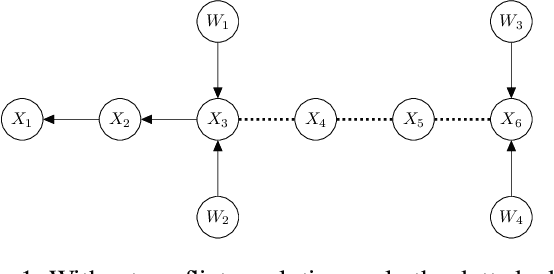
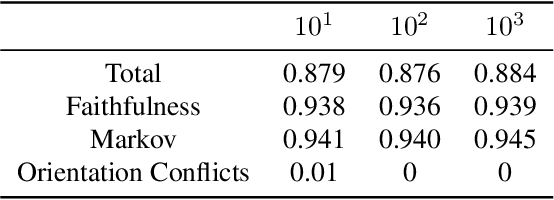
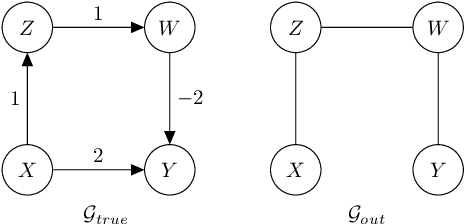
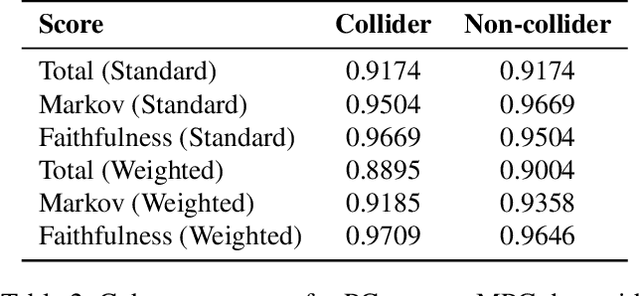
Causal discovery aims to infer causal graphs from observational or experimental data. Methods such as the popular PC algorithm are based on conditional independence testing and utilize enabling assumptions, such as the faithfulness assumption, for their inferences. In practice, these assumptions, as well as the functional assumptions inherited from the chosen conditional independence test, are typically taken as a given and not further tested for their validity on the data. In this work, we propose internal coherency scores that allow testing for assumption violations and finite sample errors, whenever detectable without requiring ground truth or further statistical tests. We provide a complete classification of erroneous results, including a distinction between detectable and undetectable errors, and prove that the detectable erroneous results can be measured by our scores. We illustrate our coherency scores on the PC algorithm with simulated and real-world datasets, and envision that testing for internal coherency can become a standard tool in applying constraint-based methods, much like a suite of tests is used to validate the assumptions of classical regression analysis.

Causal discovery with endogenous context variables

Causal systems often exhibit variations of the underlying causal mechanisms between the variables of the system. Often, these changes are driven by different environments or internal states in which the system operates, and we refer to context variables as those variables that indicate this change in causal mechanisms. An example are the causal relations in soil moisture-temperature interactions and their dependence on soil moisture regimes: Dry soil triggers a dependence of soil moisture on latent heat, while environments with wet soil do not feature such a feedback, making it a context-specific property. Crucially, a regime or context variable such as soil moisture need not be exogenous and can be influenced by the dynamical system variables - precipitation can make a dry soil wet - leading to joint systems with endogenous context variables. In this work we investigate the assumptions for constraint-based causal discovery of context-specific information in systems with endogenous context variables. We show that naive approaches such as learning different regime graphs on masked data, or pooling all data, can lead to uninformative results. We propose an adaptive constraint-based discovery algorithm and give a detailed discussion on the connection to structural causal models, including sufficiency assumptions, which allow to prove the soundness of our algorithm and to interpret the results causally. Numerical experiments demonstrate the performance of the proposed method over alternative baselines, but they also unveil current limitations of our method.

Causal Modeling in Multi-Context Systems: Distinguishing Multiple Context-Specific Causal Graphs which Account for Observational Support

Causal structure learning with data from multiple contexts carries both opportunities and challenges. Opportunities arise from considering shared and context-specific causal graphs enabling to generalize and transfer causal knowledge across contexts. However, a challenge that is currently understudied in the literature is the impact of differing observational support between contexts on the identifiability of causal graphs. Here we study in detail recently introduced [6] causal graph objects that capture both causal mechanisms and data support, allowing for the analysis of a larger class of context-specific changes, characterizing distribution shifts more precisely. We thereby extend results on the identifiability of context-specific causal structures and propose a framework to model context-specific independence (CSI) within structural causal models (SCMs) in a refined way that allows to explore scenarios where these graph objects differ. We demonstrate how this framework can help explaining phenomena like anomalies or extreme events, where causal mechanisms change or appear to change under different conditions. Our results contribute to the theoretical foundations for understanding causal relations in multi-context systems, with implications for generalization, transfer learning, and anomaly detection. Future work may extend this approach to more complex data types, such as time-series.

Causal Representation Learning in Temporal Data via Single-Parent Decoding

Scientific research often seeks to understand the causal structure underlying high-level variables in a system. For example, climate scientists study how phenomena, such as El Ni\~no, affect other climate processes at remote locations across the globe. However, scientists typically collect low-level measurements, such as geographically distributed temperature readings. From these, one needs to learn both a mapping to causally-relevant latent variables, such as a high-level representation of the El Ni\~no phenomenon and other processes, as well as the causal model over them. The challenge is that this task, called causal representation learning, is highly underdetermined from observational data alone, requiring other constraints during learning to resolve the indeterminacies. In this work, we consider a temporal model with a sparsity assumption, namely single-parent decoding: each observed low-level variable is only affected by a single latent variable. Such an assumption is reasonable in many scientific applications that require finding groups of low-level variables, such as extracting regions from geographically gridded measurement data in climate research or capturing brain regions from neural activity data. We demonstrate the identifiability of the resulting model and propose a differentiable method, Causal Discovery with Single-parent Decoding (CDSD), that simultaneously learns the underlying latents and a causal graph over them. We assess the validity of our theoretical results using simulated data and showcase the practical validity of our method in an application to real-world data from the climate science field.

Metrics on Markov Equivalence Classes for Evaluating Causal Discovery Algorithms

Many state-of-the-art causal discovery methods aim to generate an output graph that encodes the graphical separation and connection statements of the causal graph that underlies the data-generating process. In this work, we argue that an evaluation of a causal discovery method against synthetic data should include an analysis of how well this explicit goal is achieved by measuring how closely the separations/connections of the method's output align with those of the ground truth. We show that established evaluation measures do not accurately capture the difference in separations/connections of two causal graphs, and we introduce three new measures of distance called s/c-distance, Markov distance and Faithfulness distance that address this shortcoming. We complement our theoretical analysis with toy examples, empirical experiments and pseudocode.

Invariance & Causal Representation Learning: Prospects and Limitations

In causal models, a given mechanism is assumed to be invariant to changes of other mechanisms. While this principle has been utilized for inference in settings where the causal variables are observed, theoretical insights when the variables of interest are latent are largely missing. We assay the connection between invariance and causal representation learning by establishing impossibility results which show that invariance alone is insufficient to identify latent causal variables. Together with practical considerations, we use these theoretical findings to highlight the need for additional constraints in order to identify representations by exploiting invariance.

ClimateSet: A Large-Scale Climate Model Dataset for Machine Learning

Climate models have been key for assessing the impact of climate change and simulating future climate scenarios. The machine learning (ML) community has taken an increased interest in supporting climate scientists' efforts on various tasks such as climate model emulation, downscaling, and prediction tasks. Many of those tasks have been addressed on datasets created with single climate models. However, both the climate science and ML communities have suggested that to address those tasks at scale, we need large, consistent, and ML-ready climate model datasets. Here, we introduce ClimateSet, a dataset containing the inputs and outputs of 36 climate models from the Input4MIPs and CMIP6 archives. In addition, we provide a modular dataset pipeline for retrieving and preprocessing additional climate models and scenarios. We showcase the potential of our dataset by using it as a benchmark for ML-based climate model emulation. We gain new insights about the performance and generalization capabilities of the different ML models by analyzing their performance across different climate models. Furthermore, the dataset can be used to train an ML emulator on several climate models instead of just one. Such a "super emulator" can quickly project new climate change scenarios, complementing existing scenarios already provided to policymakers. We believe ClimateSet will create the basis needed for the ML community to tackle climate-related tasks at scale.

Non-parametric Conditional Independence Testing for Mixed Continuous-Categorical Variables: A Novel Method and Numerical Evaluation

Conditional independence testing (CIT) is a common task in machine learning, e.g., for variable selection, and a main component of constraint-based causal discovery. While most current CIT approaches assume that all variables are numerical or all variables are categorical, many real-world applications involve mixed-type datasets that include numerical and categorical variables. Non-parametric CIT can be conducted using conditional mutual information (CMI) estimators combined with a local permutation scheme. Recently, two novel CMI estimators for mixed-type datasets based on k-nearest-neighbors (k-NN) have been proposed. As with any k-NN method, these estimators rely on the definition of a distance metric. One approach computes distances by a one-hot encoding of the categorical variables, essentially treating categorical variables as discrete-numerical, while the other expresses CMI by entropy terms where the categorical variables appear as conditions only. In this work, we study these estimators and propose a variation of the former approach that does not treat categorical variables as numeric. Our numerical experiments show that our variant detects dependencies more robustly across different data distributions and preprocessing types.