A Monte Carlo Framework for Calibrated Uncertainty Estimation in Sequence Prediction

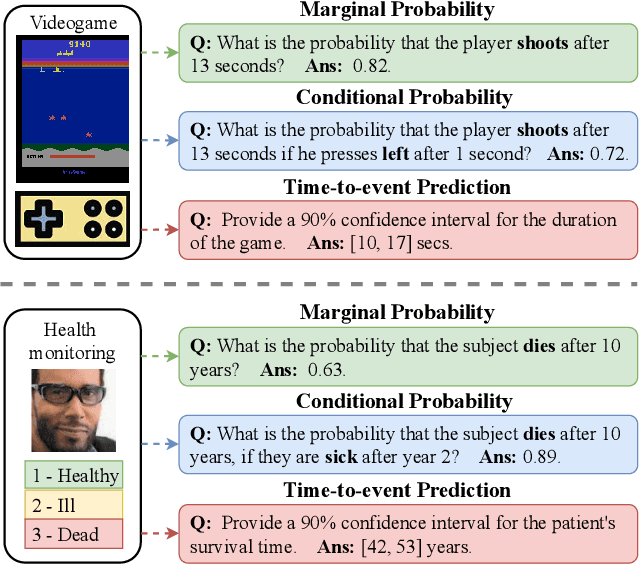
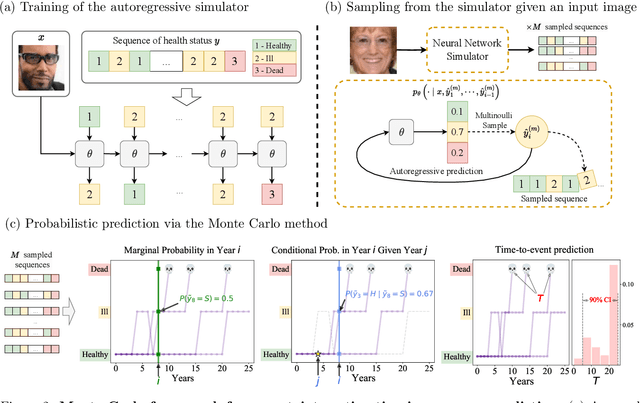
Probabilistic prediction of sequences from images and other high-dimensional data is a key challenge, particularly in risk-sensitive applications. In these settings, it is often desirable to quantify the uncertainty associated with the prediction (instead of just determining the most likely sequence, as in language modeling). In this paper, we propose a Monte Carlo framework to estimate probabilities and confidence intervals associated with the distribution of a discrete sequence. Our framework uses a Monte Carlo simulator, implemented as an autoregressively trained neural network, to sample sequences conditioned on an image input. We then use these samples to estimate the probabilities and confidence intervals. Experiments on synthetic and real data show that the framework produces accurate discriminative predictions, but can suffer from miscalibration. In order to address this shortcoming, we propose a time-dependent regularization method, which is shown to produce calibrated predictions.

Multi-modal graph neural networks for localized off-grid weather forecasting

Urgent applications like wildfire management and renewable energy generation require precise, localized weather forecasts near the Earth's surface. However, weather forecast products from machine learning or numerical weather models are currently generated on a global regular grid, on which a naive interpolation cannot accurately reflect fine-grained weather patterns close to the ground. In this work, we train a heterogeneous graph neural network (GNN) end-to-end to downscale gridded forecasts to off-grid locations of interest. This multi-modal GNN takes advantage of local historical weather observations (e.g., wind, temperature) to correct the gridded weather forecast at different lead times towards locally accurate forecasts. Each data modality is modeled as a different type of node in the graph. Using message passing, the node at the prediction location aggregates information from its heterogeneous neighbor nodes. Experiments using weather stations across the Northeastern United States show that our model outperforms a range of data-driven and non-data-driven off-grid forecasting methods. Our approach demonstrates how the gap between global large-scale weather models and locally accurate predictions can be bridged to inform localized decision-making.

Evaluating the transferability potential of deep learning models for climate downscaling

Climate downscaling, the process of generating high-resolution climate data from low-resolution simulations, is essential for understanding and adapting to climate change at regional and local scales. Deep learning approaches have proven useful in tackling this problem. However, existing studies usually focus on training models for one specific task, location and variable, which are therefore limited in their generalizability and transferability. In this paper, we evaluate the efficacy of training deep learning downscaling models on multiple diverse climate datasets to learn more robust and transferable representations. We evaluate the effectiveness of architectures zero-shot transferability using CNNs, Fourier Neural Operators (FNOs), and vision Transformers (ViTs). We assess the spatial, variable, and product transferability of downscaling models experimentally, to understand the generalizability of these different architecture types.

Fourier Neural Operators for Arbitrary Resolution Climate Data Downscaling

Climate simulations are essential in guiding our understanding of climate change and responding to its effects. However, it is computationally expensive to resolve complex climate processes at high spatial resolution. As one way to speed up climate simulations, neural networks have been used to downscale climate variables from fast-running low-resolution simulations, but high-resolution training data are often unobtainable or scarce, greatly limiting accuracy. In this work, we propose a downscaling method based on the Fourier neural operator. It trains with data of a small upsampling factor and then can zero-shot downscale its input to arbitrary unseen high resolution. Evaluated both on ERA5 climate model data and on the Navier-Stokes equation solution data, our downscaling model significantly outperforms state-of-the-art convolutional and generative adversarial downscaling models, both in standard single-resolution downscaling and in zero-shot generalization to higher upsampling factors. Furthermore, we show that our method also outperforms state-of-the-art data-driven partial differential equation solvers on Navier-Stokes equations. Overall, our work bridges the gap between simulation of a physical process and interpolation of low-resolution output, showing that it is possible to combine both approaches and significantly improve upon each other.

Generating physically-consistent high-resolution climate data with hard-constrained neural networks

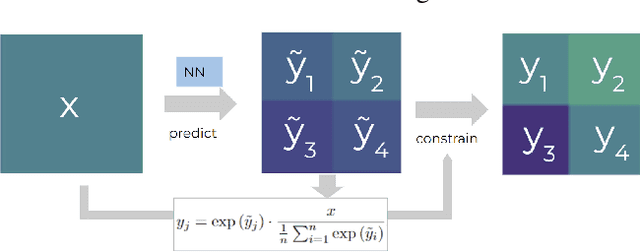
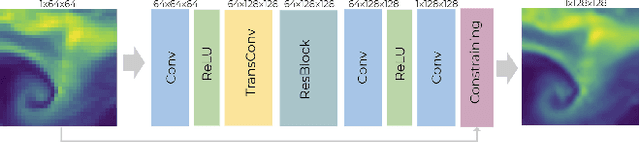
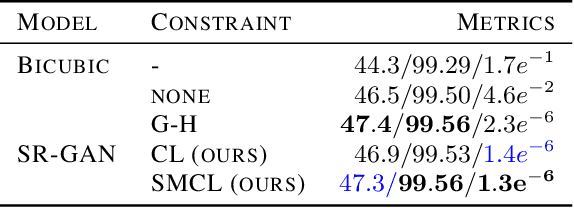
The availability of reliable, high-resolution climate and weather data is important to inform long-term decisions on climate adaptation and mitigation and to guide rapid responses to extreme events. Forecasting models are limited by computational costs and therefore often predict quantities at a coarse spatial resolution. Statistical downscaling can provide an efficient method of upsampling low-resolution data. In this field, deep learning has been applied successfully, often using methods from the super-resolution domain in computer vision. Despite often achieving visually compelling results, such models often violate conservation laws when predicting physical variables. In order to conserve important physical quantities, we develop methods that guarantee physical constraints are satisfied by a deep downscaling model while also increasing their performance according to traditional metrics. We introduce two ways of constraining the network: A renormalization layer added to the end of the neural network and a successive approach that scales with increasing upsampling factors. We show the applicability of our methods across different popular architectures and upsampling factors using ERA5 reanalysis data.