Mode-Seeking for Inverse Problems with Diffusion Models

A pre-trained unconditional diffusion model, combined with posterior sampling or maximum a posteriori (MAP) estimation techniques, can solve arbitrary inverse problems without task-specific training or fine-tuning. However, existing posterior sampling and MAP estimation methods often rely on modeling approximations and can be computationally demanding. In this work, we propose the variational mode-seeking loss (VML), which, when minimized during each reverse diffusion step, guides the generated sample towards the MAP estimate. VML arises from a novel perspective of minimizing the Kullback-Leibler (KL) divergence between the diffusion posterior $p(\mathbf{x}_0|\mathbf{x}_t)$ and the measurement posterior $p(\mathbf{x}_0|\mathbf{y})$, where $\mathbf{y}$ denotes the measurement. Importantly, for linear inverse problems, VML can be analytically derived and need not be approximated. Based on further theoretical insights, we propose VML-MAP, an empirically effective algorithm for solving inverse problems, and validate its efficacy over existing methods in both performance and computational time, through extensive experiments on diverse image-restoration tasks across multiple datasets.

Shocks Under Control: Taming Transonic Compressible Flow over an RAE2822 Airfoil with Deep Reinforcement Learning

Active flow control of compressible transonic shock-boundary layer interactions over a two-dimensional RAE2822 airfoil at Re = 50,000 is investigated using deep reinforcement learning (DRL). The flow field exhibits highly unsteady dynamics, including complex shock-boundary layer interactions, shock oscillations, and the generation of Kutta waves from the trailing edge. A high-fidelity CFD solver, employing a fifth-order spectral discontinuous Galerkin scheme in space and a strong-stability-preserving Runge-Kutta (5,4) method in time, together with adaptive mesh refinement capability, is used to obtain the accurate flow field. Synthetic jet actuation is employed to manipulate these unsteady flow features, while the DRL agent autonomously discovers effective control strategies through direct interaction with high-fidelity compressible flow simulations. The trained controllers effectively mitigate shock-induced separation, suppress unsteady oscillations, and manipulate aerodynamic forces under transonic conditions. In the first set of experiments, aimed at both drag reduction and lift enhancement, the DRL-based control reduces the average drag coefficient by 13.78% and increases lift by 131.18%, thereby improving the lift-to-drag ratio by 121.52%, which underscores its potential for managing complex flow dynamics. In the second set, targeting drag reduction while maintaining lift, the DRL-based control achieves a 25.62% reduction in drag and a substantial 196.30% increase in lift, accompanied by markedly diminished oscillations. In this case, the lift-to-drag ratio improves by 220.26%.

Efficient probabilistic surrogate modeling techniques for partially-observed large-scale dynamical systems

This paper is concerned with probabilistic techniques for forecasting dynamical systems described by partial differential equations (such as, for example, the Navier-Stokes equations). In particular, it is investigating and comparing various extensions to the flow matching paradigm that reduce the number of sampling steps. In this regard, it compares direct distillation, progressive distillation, adversarial diffusion distillation, Wasserstein GANs and rectified flows. Moreover, experiments are conducted on a set of challenging systems. In particular, we also address the challenge of directly predicting 2D slices of large-scale 3D simulations, paving the way for efficient inflow generation for solvers.

Deep Learning-Driven Downscaling for Climate Risk Assessment of Projected Temperature Extremes in the Nordic Region

Rapid changes and increasing climatic variability across the widely varied Koppen-Geiger regions of northern Europe generate significant needs for adaptation. Regional planning needs high-resolution projected temperatures. This work presents an integrative downscaling framework that incorporates Vision Transformer (ViT), Convolutional Long Short-Term Memory (ConvLSTM), and Geospatial Spatiotemporal Transformer with Attention and Imbalance-Aware Network (GeoStaNet) models. The framework is evaluated with a multicriteria decision system, Deep Learning-TOPSIS (DL-TOPSIS), for ten strategically chosen meteorological stations encompassing the temperate oceanic (Cfb), subpolar oceanic (Cfc), warm-summer continental (Dfb), and subarctic (Dfc) climate regions. Norwegian Earth System Model (NorESM2-LM) Coupled Model Intercomparison Project Phase 6 (CMIP6) outputs were bias-corrected during the 1951-2014 period and subsequently validated against earlier observations of day-to-day temperature metrics and diurnal range statistics. The ViT showed improved performance (Root Mean Squared Error (RMSE): 1.01 degrees C; R^2: 0.92), allowing for production of credible downscaled projections. Under the SSP5-8.5 scenario, the Dfc and Dfb climate zones are projected to warm by 4.8 degrees C and 3.9 degrees C, respectively, by 2100, with expansion in the diurnal temperature range by more than 1.5 degrees C. The Time of Emergence signal first appears in subarctic winter seasons (Dfc: approximately 2032), signifying an urgent need for adaptation measures. The presented framework offers station-based, high-resolution estimates of uncertainties and extremes, with direct uses for adaptation policy over high-latitude regions with fast environmental change.

Potential and challenges of generative adversarial networks for super-resolution in 4D Flow MRI

4D Flow Magnetic Resonance Imaging (4D Flow MRI) enables non-invasive quantification of blood flow and hemodynamic parameters. However, its clinical application is limited by low spatial resolution and noise, particularly affecting near-wall velocity measurements. Machine learning-based super-resolution has shown promise in addressing these limitations, but challenges remain, not least in recovering near-wall velocities. Generative adversarial networks (GANs) offer a compelling solution, having demonstrated strong capabilities in restoring sharp boundaries in non-medical super-resolution tasks. Yet, their application in 4D Flow MRI remains unexplored, with implementation challenged by known issues such as training instability and non-convergence. In this study, we investigate GAN-based super-resolution in 4D Flow MRI. Training and validation were conducted using patient-specific cerebrovascular in-silico models, converted into synthetic images via an MR-true reconstruction pipeline. A dedicated GAN architecture was implemented and evaluated across three adversarial loss functions: Vanilla, Relativistic, and Wasserstein. Our results demonstrate that the proposed GAN improved near-wall velocity recovery compared to a non-adversarial reference (vNRMSE: 6.9% vs. 9.6%); however, that implementation specifics are critical for stable network training. While Vanilla and Relativistic GANs proved unstable compared to generator-only training (vNRMSE: 8.1% and 7.8% vs. 7.2%), a Wasserstein GAN demonstrated optimal stability and incremental improvement (vNRMSE: 6.9% vs. 7.2%). The Wasserstein GAN further outperformed the generator-only baseline at low SNR (vNRMSE: 8.7% vs. 10.7%). These findings highlight the potential of GAN-based super-resolution in enhancing 4D Flow MRI, particularly in challenging cerebrovascular regions, while emphasizing the need for careful selection of adversarial strategies.

Evaluating Visual Mathematics in Multimodal LLMs: A Multilingual Benchmark Based on the Kangaroo Tests

Multimodal Large Language Models (MLLMs) promise advanced vision language capabilities, yet their effectiveness in visually presented mathematics remains underexplored. This paper analyzes the development and evaluation of MLLMs for mathematical problem solving, focusing on diagrams, multilingual text, and symbolic notation. We then assess several models, including GPT 4o, Pixtral, Qwen VL, Llama 3.2 Vision variants, and Gemini 2.0 Flash in a multilingual Kangaroo style benchmark spanning English, French, Spanish, and Catalan. Our experiments reveal four key findings. First, overall precision remains moderate across geometry, visual algebra, logic, patterns, and combinatorics: no single model excels in every topic. Second, while most models see improved accuracy with questions that do not have images, the gain is often limited; performance for some remains nearly unchanged without visual input, indicating underutilization of diagrammatic information. Third, substantial variation exists across languages and difficulty levels: models frequently handle easier items but struggle with advanced geometry and combinatorial reasoning. Notably, Gemini 2.0 Flash achieves the highest precision on image based tasks, followed by Qwen VL 2.5 72B and GPT 4o, though none approach human level performance. Fourth, a complementary analysis aimed at distinguishing whether models reason or simply recite reveals that Gemini and GPT 4o stand out for their structured reasoning and consistent accuracy. In contrast, Pixtral and Llama exhibit less consistent reasoning, often defaulting to heuristics or randomness when unable to align their outputs with the given answer options.

Regional climate projections using a deep-learning-based model-ranking and downscaling framework: Application to European climate zones

Accurate regional climate forecast calls for high-resolution downscaling of Global Climate Models (GCMs). This work presents a deep-learning-based multi-model evaluation and downscaling framework ranking 32 Coupled Model Intercomparison Project Phase 6 (CMIP6) models using a Deep Learning-TOPSIS (DL-TOPSIS) mechanism and so refines outputs using advanced deep-learning models. Using nine performance criteria, five K\"oppen-Geiger climate zones -- Tropical, Arid, Temperate, Continental, and Polar -- are investigated over four seasons. While TaiESM1 and CMCC-CM2-SR5 show notable biases, ranking results show that NorESM2-LM, GISS-E2-1-G, and HadGEM3-GC31-LL outperform other models. Four models contribute to downscaling the top-ranked GCMs to 0.1$^{\circ}$ resolution: Vision Transformer (ViT), Geospatial Spatiotemporal Transformer with Attention and Imbalance-Aware Network (GeoSTANet), CNN-LSTM, and CNN-Long Short-Term Memory (ConvLSTM). Effectively capturing temperature extremes (TXx, TNn), GeoSTANet achieves the highest accuracy (Root Mean Square Error (RMSE) = 1.57$^{\circ}$C, Kling-Gupta Efficiency (KGE) = 0.89, Nash-Sutcliffe Efficiency (NSE) = 0.85, Correlation ($r$) = 0.92), so reducing RMSE by 20% over ConvLSTM. CNN-LSTM and ConvLSTM do well in Continental and Temperate zones; ViT finds fine-scale temperature fluctuations difficult. These results confirm that multi-criteria ranking improves GCM selection for regional climate studies and transformer-based downscaling exceeds conventional deep-learning methods. This framework offers a scalable method to enhance high-resolution climate projections, benefiting impact assessments and adaptation plans.

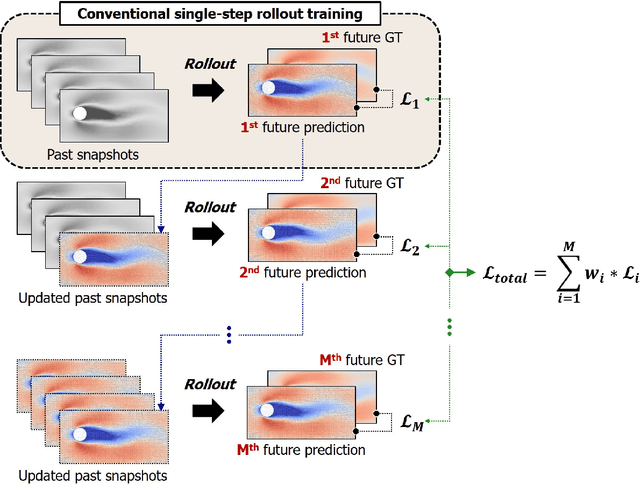
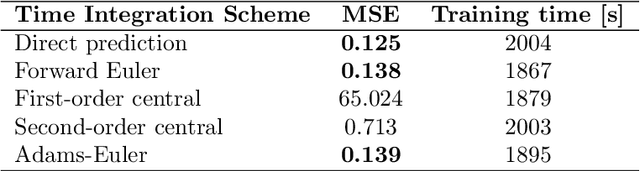
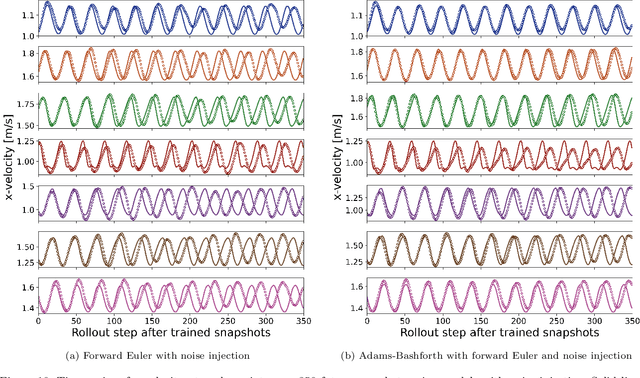
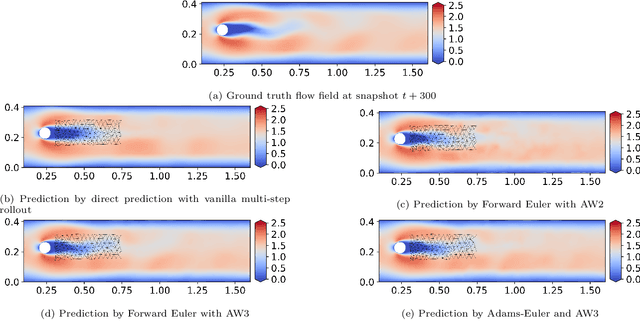
Towards Robust Spatio-Temporal Auto-Regressive Prediction: Adams-Bashforth Time Integration with Adaptive Multi-Step Rollout

This study addresses the critical challenge of error accumulation in spatio-temporal auto-regressive predictions within scientific machine learning models by introducing innovative temporal integration schemes and adaptive multi-step rollout strategies. We present a comprehensive analysis of time integration methods, highlighting the adaptation of the two-step Adams-Bashforth scheme to enhance long-term prediction robustness in auto-regressive models. Additionally, we improve temporal prediction accuracy through a multi-step rollout strategy that incorporates multiple future time steps during training, supported by three newly proposed approaches that dynamically adjust the importance of each future step. By integrating the Adams-Bashforth scheme with adaptive multi-step strategies, our graph neural network-based auto-regressive model accurately predicts 350 future time steps, even under practical constraints such as limited training data and minimal model capacity -- achieving an error of only 1.6% compared to the vanilla auto-regressive approach. Moreover, our framework demonstrates an 83% improvement in rollout performance over the standard noise injection method, a standard technique for enhancing long-term rollout performance. Its effectiveness is further validated in more challenging scenarios with truncated meshes, showcasing its adaptability and robustness in practical applications. This work introduces a versatile framework for robust long-term spatio-temporal auto-regressive predictions, effectively mitigating error accumulation across various model types and engineering discipline.

Transformer-Based Fault-Tolerant Control for Fixed-Wing UAVs Using Knowledge Distillation and In-Context Adaptation

This study presents a transformer-based approach for fault-tolerant control in fixed-wing Unmanned Aerial Vehicles (UAVs), designed to adapt in real time to dynamic changes caused by structural damage or actuator failures. Unlike traditional Flight Control Systems (FCSs) that rely on classical control theory and struggle under severe alterations in dynamics, our method directly maps outer-loop reference values -- altitude, heading, and airspeed -- into control commands using the in-context learning and attention mechanisms of transformers, thus bypassing inner-loop controllers and fault-detection layers. Employing a teacher-student knowledge distillation framework, the proposed approach trains a student agent with partial observations by transferring knowledge from a privileged expert agent with full observability, enabling robust performance across diverse failure scenarios. Experimental results demonstrate that our transformer-based controller outperforms industry-standard FCS and state-of-the-art reinforcement learning (RL) methods, maintaining high tracking accuracy and stability in nominal conditions and extreme failure cases, highlighting its potential for enhancing UAV operational safety and reliability.

Navigation in a simplified Urban Flow through Deep Reinforcement Learning

The increasing number of unmanned aerial vehicles (UAVs) in urban environments requires a strategy to minimize their environmental impact, both in terms of energy efficiency and noise reduction. In order to reduce these concerns, novel strategies for developing prediction models and optimization of flight planning, for instance through deep reinforcement learning (DRL), are needed. Our goal is to develop DRL algorithms capable of enabling the autonomous navigation of UAVs in urban environments, taking into account the presence of buildings and other UAVs, optimizing the trajectories in order to reduce both energetic consumption and noise. This is achieved using fluid-flow simulations which represent the environment in which UAVs navigate and training the UAV as an agent interacting with an urban environment. In this work, we consider a domain domain represented by a two-dimensional flow field with obstacles, ideally representing buildings, extracted from a three-dimensional high-fidelity numerical simulation. The presented methodology, using PPO+LSTM cells, was validated by reproducing a simple but fundamental problem in navigation, namely the Zermelo's problem, which deals with a vessel navigating in a turbulent flow, travelling from a starting point to a target location, optimizing the trajectory. The current method shows a significant improvement with respect to both a simple PPO and a TD3 algorithm, with a success rate (SR) of the PPO+LSTM trained policy of 98.7%, and a crash rate (CR) of 0.1%, outperforming both PPO (SR = 75.6%, CR=18.6%) and TD3 (SR=77.4% and CR=14.5%). This is the first step towards DRL strategies which will guide UAVs in a three-dimensional flow field using real-time signals, making the navigation efficient in terms of flight time and avoiding damages to the vehicle.