Revisiting Score Function Estimators for $k$-Subset Sampling

Are score function estimators an underestimated approach to learning with $k$-subset sampling? Sampling $k$-subsets is a fundamental operation in many machine learning tasks that is not amenable to differentiable parametrization, impeding gradient-based optimization. Prior work has focused on relaxed sampling or pathwise gradient estimators. Inspired by the success of score function estimators in variational inference and reinforcement learning, we revisit them within the context of $k$-subset sampling. Specifically, we demonstrate how to efficiently compute the $k$-subset distribution's score function using a discrete Fourier transform, and reduce the estimator's variance with control variates. The resulting estimator provides both exact samples and unbiased gradient estimates while also applying to non-differentiable downstream models, unlike existing methods. Experiments in feature selection show results competitive with current methods, despite weaker assumptions.

Indirectly Parameterized Concrete Autoencoders

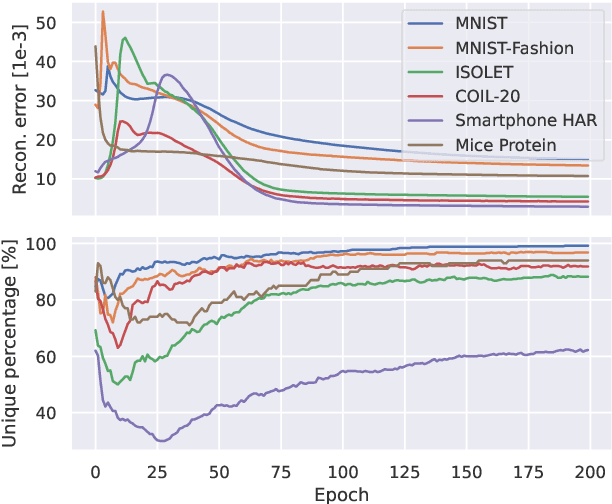
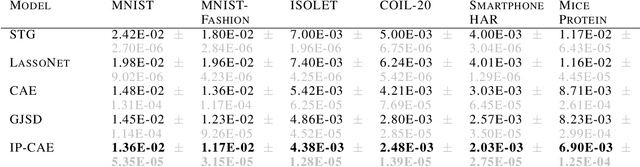
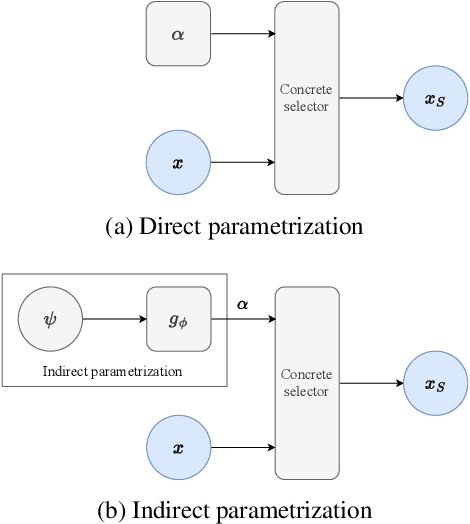
Feature selection is a crucial task in settings where data is high-dimensional or acquiring the full set of features is costly. Recent developments in neural network-based embedded feature selection show promising results across a wide range of applications. Concrete Autoencoders (CAEs), considered state-of-the-art in embedded feature selection, may struggle to achieve stable joint optimization, hurting their training time and generalization. In this work, we identify that this instability is correlated with the CAE learning duplicate selections. To remedy this, we propose a simple and effective improvement: Indirectly Parameterized CAEs (IP-CAEs). IP-CAEs learn an embedding and a mapping from it to the Gumbel-Softmax distributions' parameters. Despite being simple to implement, IP-CAE exhibits significant and consistent improvements over CAE in both generalization and training time across several datasets for reconstruction and classification. Unlike CAE, IP-CAE effectively leverages non-linear relationships and does not require retraining the jointly optimized decoder. Furthermore, our approach is, in principle, generalizable to Gumbel-Softmax distributions beyond feature selection.