Efficient Mixture Learning in Black-Box Variational Inference

Mixture variational distributions in black box variational inference (BBVI) have demonstrated impressive results in challenging density estimation tasks. However, currently scaling the number of mixture components can lead to a linear increase in the number of learnable parameters and a quadratic increase in inference time due to the evaluation of the evidence lower bound (ELBO). Our two key contributions address these limitations. First, we introduce the novel Multiple Importance Sampling Variational Autoencoder (MISVAE), which amortizes the mapping from input to mixture-parameter space using one-hot encodings. Fortunately, with MISVAE, each additional mixture component incurs a negligible increase in network parameters. Second, we construct two new estimators of the ELBO for mixtures in BBVI, enabling a tremendous reduction in inference time with marginal or even improved impact on performance. Collectively, our contributions enable scalability to hundreds of mixture components and provide superior estimation performance in shorter time, with fewer network parameters compared to previous Mixture VAEs. Experimenting with MISVAE, we achieve astonishing, SOTA results on MNIST. Furthermore, we empirically validate our estimators in other BBVI settings, including Bayesian phylogenetic inference, where we improve inference times for the SOTA mixture model on eight data sets.

Indirectly Parameterized Concrete Autoencoders

Feature selection is a crucial task in settings where data is high-dimensional or acquiring the full set of features is costly. Recent developments in neural network-based embedded feature selection show promising results across a wide range of applications. Concrete Autoencoders (CAEs), considered state-of-the-art in embedded feature selection, may struggle to achieve stable joint optimization, hurting their training time and generalization. In this work, we identify that this instability is correlated with the CAE learning duplicate selections. To remedy this, we propose a simple and effective improvement: Indirectly Parameterized CAEs (IP-CAEs). IP-CAEs learn an embedding and a mapping from it to the Gumbel-Softmax distributions' parameters. Despite being simple to implement, IP-CAE exhibits significant and consistent improvements over CAE in both generalization and training time across several datasets for reconstruction and classification. Unlike CAE, IP-CAE effectively leverages non-linear relationships and does not require retraining the jointly optimized decoder. Furthermore, our approach is, in principle, generalizable to Gumbel-Softmax distributions beyond feature selection.

Improved Variational Bayesian Phylogenetic Inference using Mixtures

We present VBPI-Mixtures, an algorithm designed to enhance the accuracy of phylogenetic posterior distributions, particularly for tree-topology and branch-length approximations. Despite the Variational Bayesian Phylogenetic Inference (VBPI), a leading-edge black-box variational inference (BBVI) framework, achieving remarkable approximations of these distributions, the multimodality of the tree-topology posterior presents a formidable challenge to sampling-based learning techniques such as BBVI. Advanced deep learning methodologies such as normalizing flows and graph neural networks have been explored to refine the branch-length posterior approximation, yet efforts to ameliorate the posterior approximation over tree topologies have been lacking. Our novel VBPI-Mixtures algorithm bridges this gap by harnessing the latest breakthroughs in mixture learning within the BBVI domain. As a result, VBPI-Mixtures is capable of capturing distributions over tree-topologies that VBPI fails to model. We deliver state-of-the-art performance on difficult density estimation tasks across numerous real phylogenetic datasets.

Statistical Distance Based Deterministic Offspring Selection in SMC Methods

Over the years, sequential Monte Carlo (SMC) and, equivalently, particle filter (PF) theory has gained substantial attention from researchers. However, the performance of the resampling methodology, also known as offspring selection, has not advanced recently. We propose two deterministic offspring selection methods, which strive to minimize the Kullback-Leibler (KL) divergence and the total variation (TV) distance, respectively, between the particle distribution prior and subsequent to the offspring selection. By reducing the statistical distance between the selected offspring and the joint distribution, we obtain a heuristic search procedure that performs superior to a maximum likelihood search in precisely those contexts where the latter performs better than an SMC. For SMC and particle Markov chain Monte Carlo (pMCMC), our proposed offspring selection methods always outperform or compare favorably with the two state-of-the-art resampling schemes on two models commonly used as benchmarks from the literature.

Learning with MISELBO: The Mixture Cookbook

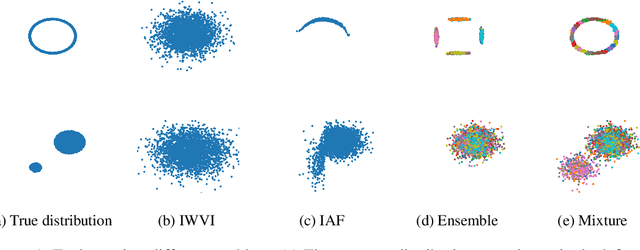
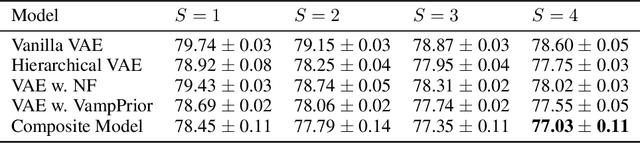
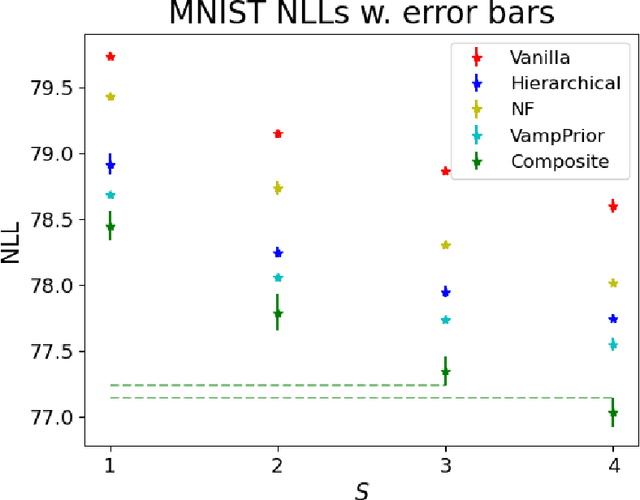
Mixture models in variational inference (VI) is an active field of research. Recent works have established their connection to multiple importance sampling (MIS) through the MISELBO and advanced the use of ensemble approximations for large-scale problems. However, as we show here, an independent learning of the ensemble components can lead to suboptimal diversity. Hence, we study the effect of instead using MISELBO as an objective function for learning mixtures, and we propose the first ever mixture of variational approximations for a normalizing flow-based hierarchical variational autoencoder (VAE) with VampPrior and a PixelCNN decoder network. Two major insights led to the construction of this novel composite model. First, mixture models have potential to be off-the-shelf tools for practitioners to obtain more flexible posterior approximations in VAEs. Therefore, we make them more accessible by demonstrating how to apply them to four popular architectures. Second, the mixture components cooperate in order to cover the target distribution while trying to maximize their diversity when MISELBO is the objective function. We explain this cooperative behavior by drawing a novel connection between VI and adaptive importance sampling. Finally, we demonstrate the superiority of the Mixture VAEs' learned feature representations on both image and single-cell transcriptome data, and obtain state-of-the-art results among VAE architectures in terms of negative log-likelihood on the MNIST and FashionMNIST datasets. Code available here: \url{https://github.com/Lagergren-Lab/MixtureVAEs}.

VaiPhy: a Variational Inference Based Algorithm for Phylogeny

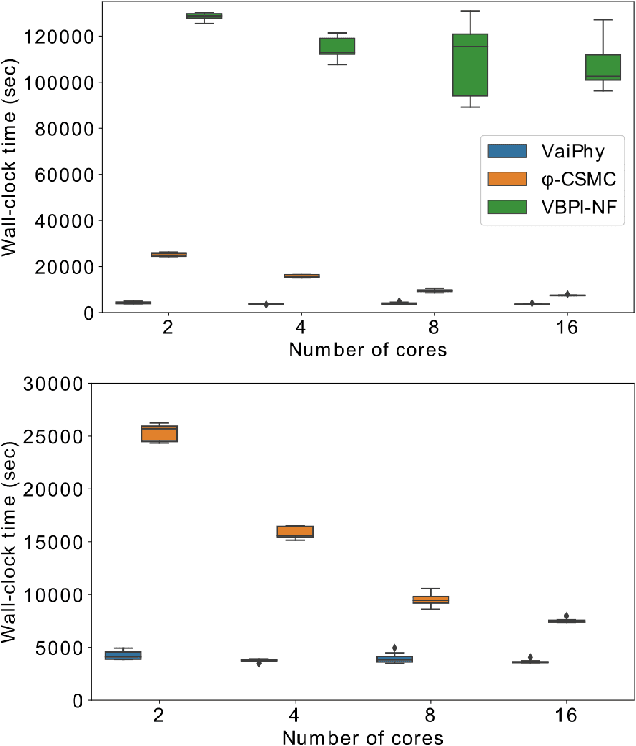
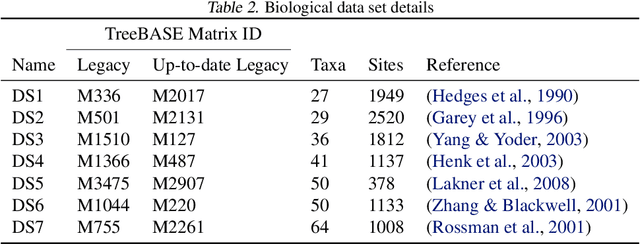
Phylogenetics is a classical methodology in computational biology that today has become highly relevant for medical investigation of single-cell data, e.g., in the context of development of cancer. The exponential size of the tree space is unfortunately a formidable obstacle for current Bayesian phylogenetic inference using Markov chain Monte Carlo based methods since these rely on local operations. And although more recent variational inference (VI) based methods offer speed improvements, they rely on expensive auto-differentiation operations for learning the variational parameters. We propose VaiPhy, a remarkably fast VI based algorithm for approximate posterior inference in an augmented tree space. VaiPhy produces marginal log-likelihood estimates on par with the state-of-the-art methods on real data, and is considerably faster since it does not require auto-differentiation. Instead, VaiPhy combines coordinate ascent update equations with two novel sampling schemes: (i) SLANTIS, a proposal distribution for tree topologies in the augmented tree space, and (ii) the JC sampler, the, to the best of our knowledge, first ever scheme for sampling branch lengths directly from the popular Jukes-Cantor model. We compare VaiPhy in terms of density estimation and runtime. Additionally, we evaluate the reproducibility of the baselines. We provide our code on GitHub: https://github.com/Lagergren-Lab/VaiPhy.

Multiple Importance Sampling ELBO and Deep Ensembles of Variational Approximations

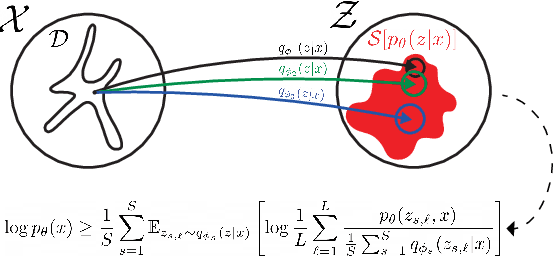
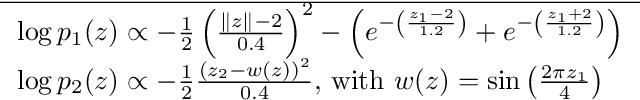
In variational inference (VI), the marginal log-likelihood is estimated using the standard evidence lower bound (ELBO), or improved versions as the importance weighted ELBO (IWELBO). We propose the multiple importance sampling ELBO (MISELBO), a \textit{versatile} yet \textit{simple} framework. MISELBO is applicable in both amortized and classical VI, and it uses ensembles, e.g., deep ensembles, of independently inferred variational approximations. As far as we are aware, the concept of deep ensembles in amortized VI has not previously been established. We prove that MISELBO provides a tighter bound than the average of standard ELBOs, and demonstrate empirically that it gives tighter bounds than the average of IWELBOs. MISELBO is evaluated in density-estimation experiments that include MNIST and several real-data phylogenetic tree inference problems. First, on the MNIST dataset, MISELBO boosts the density-estimation performances of a state-of-the-art model, nouveau VAE. Second, in the phylogenetic tree inference setting, our framework enhances a state-of-the-art VI algorithm that uses normalizing flows. On top of the technical benefits of MISELBO, it allows to unveil connections between VI and recent advances in the importance sampling literature, paving the way for further methodological advances. We provide our code at \url{https://github.com/Lagergren-Lab/MISELBO}.