Statistical Distance Based Deterministic Offspring Selection in SMC Methods

Over the years, sequential Monte Carlo (SMC) and, equivalently, particle filter (PF) theory has gained substantial attention from researchers. However, the performance of the resampling methodology, also known as offspring selection, has not advanced recently. We propose two deterministic offspring selection methods, which strive to minimize the Kullback-Leibler (KL) divergence and the total variation (TV) distance, respectively, between the particle distribution prior and subsequent to the offspring selection. By reducing the statistical distance between the selected offspring and the joint distribution, we obtain a heuristic search procedure that performs superior to a maximum likelihood search in precisely those contexts where the latter performs better than an SMC. For SMC and particle Markov chain Monte Carlo (pMCMC), our proposed offspring selection methods always outperform or compare favorably with the two state-of-the-art resampling schemes on two models commonly used as benchmarks from the literature.

VaiPhy: a Variational Inference Based Algorithm for Phylogeny

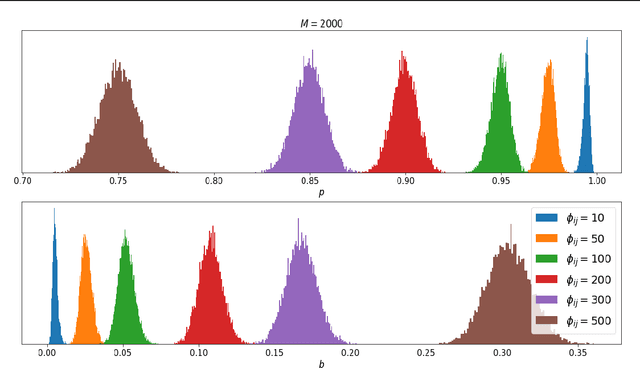
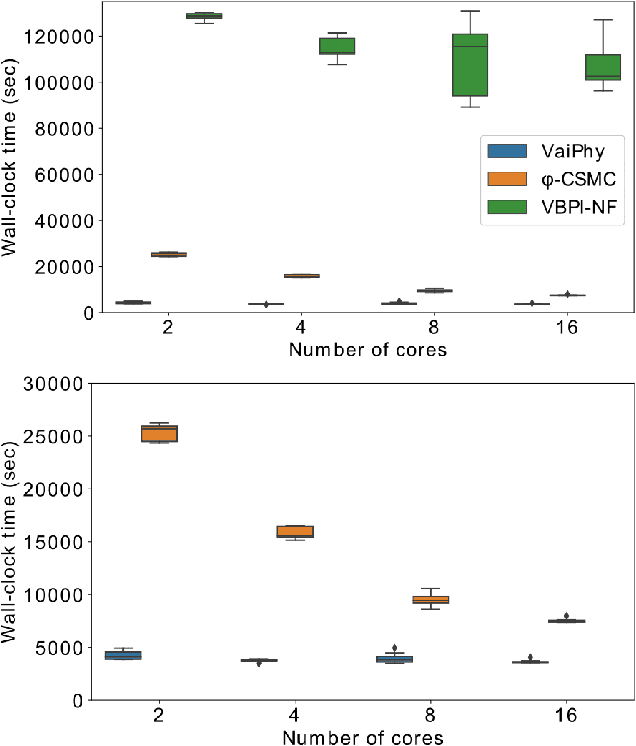
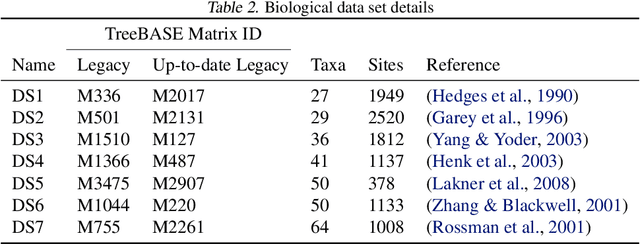
Phylogenetics is a classical methodology in computational biology that today has become highly relevant for medical investigation of single-cell data, e.g., in the context of development of cancer. The exponential size of the tree space is unfortunately a formidable obstacle for current Bayesian phylogenetic inference using Markov chain Monte Carlo based methods since these rely on local operations. And although more recent variational inference (VI) based methods offer speed improvements, they rely on expensive auto-differentiation operations for learning the variational parameters. We propose VaiPhy, a remarkably fast VI based algorithm for approximate posterior inference in an augmented tree space. VaiPhy produces marginal log-likelihood estimates on par with the state-of-the-art methods on real data, and is considerably faster since it does not require auto-differentiation. Instead, VaiPhy combines coordinate ascent update equations with two novel sampling schemes: (i) SLANTIS, a proposal distribution for tree topologies in the augmented tree space, and (ii) the JC sampler, the, to the best of our knowledge, first ever scheme for sampling branch lengths directly from the popular Jukes-Cantor model. We compare VaiPhy in terms of density estimation and runtime. Additionally, we evaluate the reproducibility of the baselines. We provide our code on GitHub: https://github.com/Lagergren-Lab/VaiPhy.

Multiple Importance Sampling ELBO and Deep Ensembles of Variational Approximations

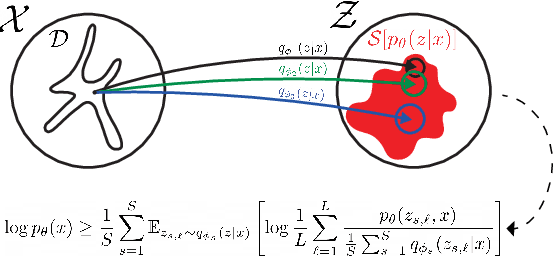
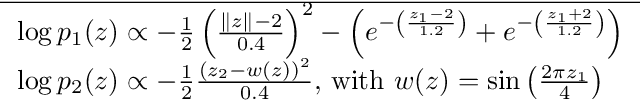
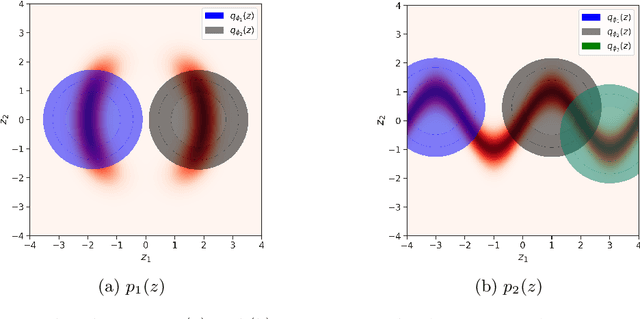
In variational inference (VI), the marginal log-likelihood is estimated using the standard evidence lower bound (ELBO), or improved versions as the importance weighted ELBO (IWELBO). We propose the multiple importance sampling ELBO (MISELBO), a \textit{versatile} yet \textit{simple} framework. MISELBO is applicable in both amortized and classical VI, and it uses ensembles, e.g., deep ensembles, of independently inferred variational approximations. As far as we are aware, the concept of deep ensembles in amortized VI has not previously been established. We prove that MISELBO provides a tighter bound than the average of standard ELBOs, and demonstrate empirically that it gives tighter bounds than the average of IWELBOs. MISELBO is evaluated in density-estimation experiments that include MNIST and several real-data phylogenetic tree inference problems. First, on the MNIST dataset, MISELBO boosts the density-estimation performances of a state-of-the-art model, nouveau VAE. Second, in the phylogenetic tree inference setting, our framework enhances a state-of-the-art VI algorithm that uses normalizing flows. On top of the technical benefits of MISELBO, it allows to unveil connections between VI and recent advances in the importance sampling literature, paving the way for further methodological advances. We provide our code at \url{https://github.com/Lagergren-Lab/MISELBO}.

HAMSI: A Parallel Incremental Optimization Algorithm Using Quadratic Approximations for Solving Partially Separable Problems

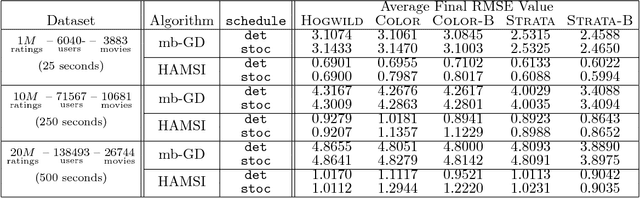
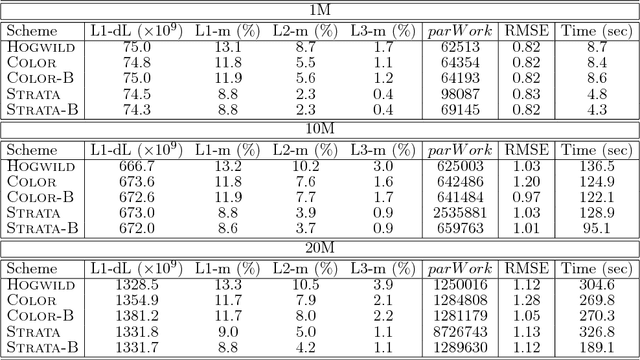
We propose HAMSI (Hessian Approximated Multiple Subsets Iteration), which is a provably convergent, second order incremental algorithm for solving large-scale partially separable optimization problems. The algorithm is based on a local quadratic approximation, and hence, allows incorporating curvature information to speed-up the convergence. HAMSI is inherently parallel and it scales nicely with the number of processors. Combined with techniques for effectively utilizing modern parallel computer architectures, we illustrate that the proposed method converges more rapidly than a parallel stochastic gradient descent when both methods are used to solve large-scale matrix factorization problems. This performance gain comes only at the expense of using memory that scales linearly with the total size of the optimization variables. We conclude that HAMSI may be considered as a viable alternative in many large scale problems, where first order methods based on variants of stochastic gradient descent are applicable.

Parallel Stochastic Gradient Markov Chain Monte Carlo for Matrix Factorisation Models

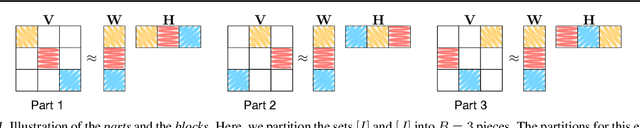
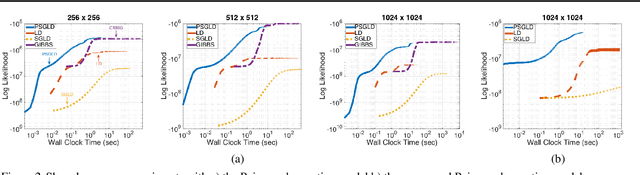
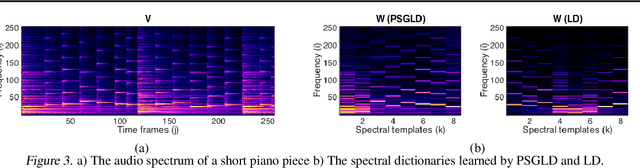
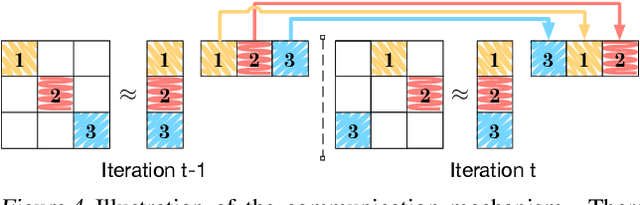
For large matrix factorisation problems, we develop a distributed Markov Chain Monte Carlo (MCMC) method based on stochastic gradient Langevin dynamics (SGLD) that we call Parallel SGLD (PSGLD). PSGLD has very favourable scaling properties with increasing data size and is comparable in terms of computational requirements to optimisation methods based on stochastic gradient descent. PSGLD achieves high performance by exploiting the conditional independence structure of the MF models to sub-sample data in a systematic manner as to allow parallelisation and distributed computation. We provide a convergence proof of the algorithm and verify its superior performance on various architectures such as Graphics Processing Units, shared memory multi-core systems and multi-computer clusters.