Differentially Private Accelerated Optimization Algorithms

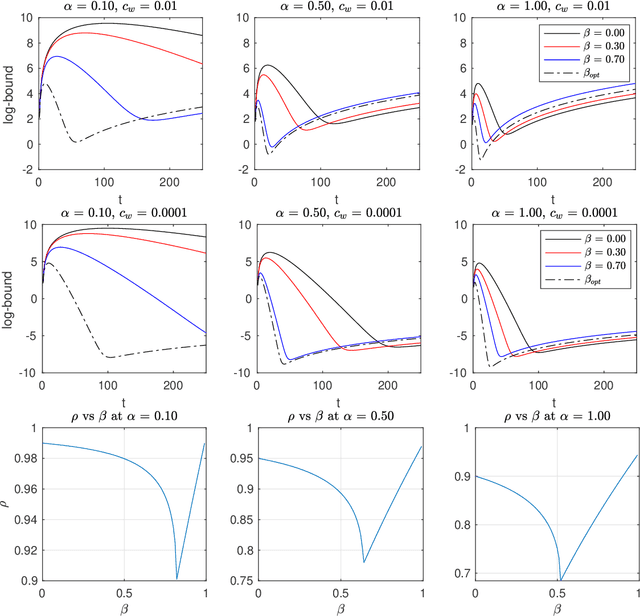
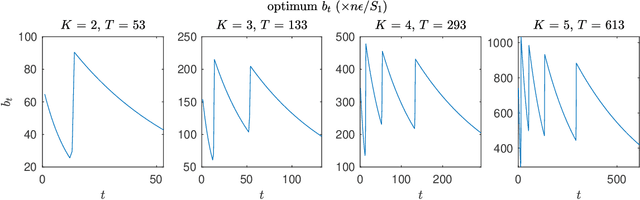
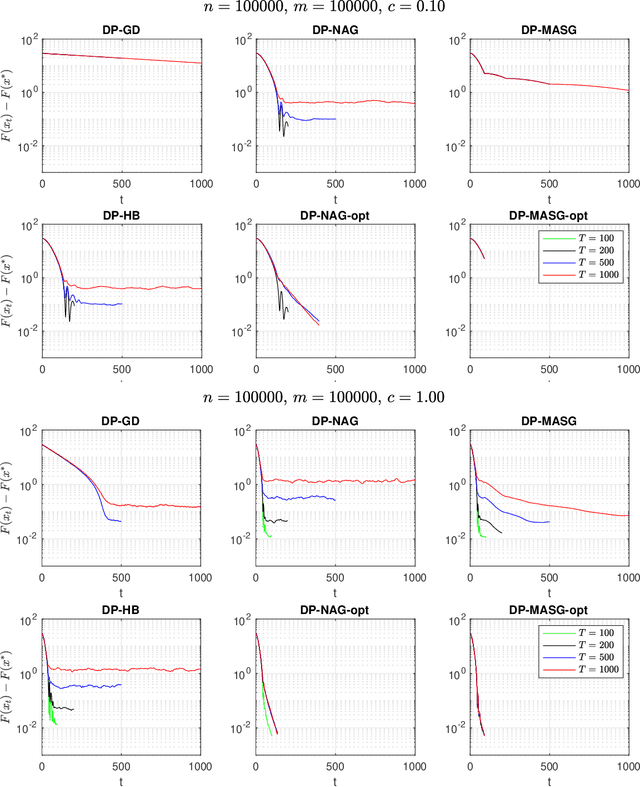
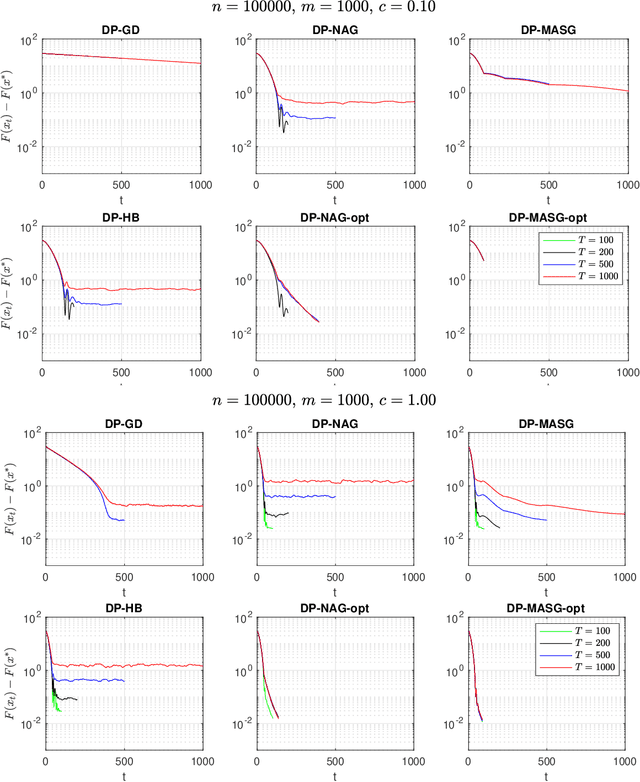
We present two classes of differentially private optimization algorithms derived from the well-known accelerated first-order methods. The first algorithm is inspired by Polyak's heavy ball method and employs a smoothing approach to decrease the accumulated noise on the gradient steps required for differential privacy. The second class of algorithms are based on Nesterov's accelerated gradient method and its recent multi-stage variant. We propose a noise dividing mechanism for the iterations of Nesterov's method in order to improve the error behavior of the algorithm. The convergence rate analyses are provided for both the heavy ball and the Nesterov's accelerated gradient method with the help of the dynamical system analysis techniques. Finally, we conclude with our numerical experiments showing that the presented algorithms have advantages over the well-known differentially private algorithms.

HAMSI: A Parallel Incremental Optimization Algorithm Using Quadratic Approximations for Solving Partially Separable Problems

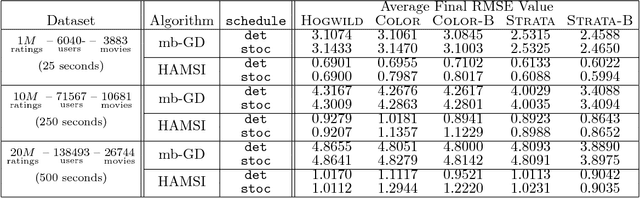
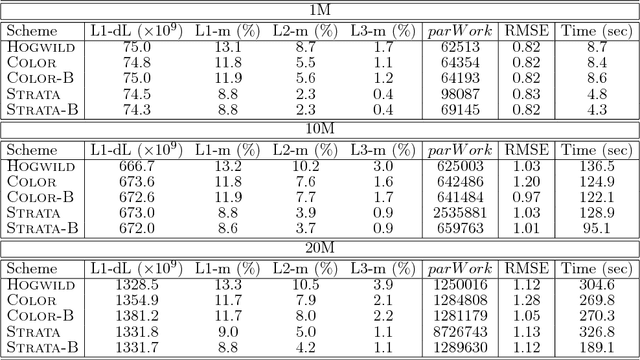
We propose HAMSI (Hessian Approximated Multiple Subsets Iteration), which is a provably convergent, second order incremental algorithm for solving large-scale partially separable optimization problems. The algorithm is based on a local quadratic approximation, and hence, allows incorporating curvature information to speed-up the convergence. HAMSI is inherently parallel and it scales nicely with the number of processors. Combined with techniques for effectively utilizing modern parallel computer architectures, we illustrate that the proposed method converges more rapidly than a parallel stochastic gradient descent when both methods are used to solve large-scale matrix factorization problems. This performance gain comes only at the expense of using memory that scales linearly with the total size of the optimization variables. We conclude that HAMSI may be considered as a viable alternative in many large scale problems, where first order methods based on variants of stochastic gradient descent are applicable.