Adaptive Online Bayesian Estimation of Frequency Distributions with Local Differential Privacy

We propose a novel Bayesian approach for the adaptive and online estimation of the frequency distribution of a finite number of categories under the local differential privacy (LDP) framework. The proposed algorithm performs Bayesian parameter estimation via posterior sampling and adapts the randomization mechanism for LDP based on the obtained posterior samples. We propose a randomized mechanism for LDP which uses a subset of categories as an input and whose performance depends on the selected subset and the true frequency distribution. By using the posterior sample as an estimate of the frequency distribution, the algorithm performs a computationally tractable subset selection step to maximize the utility of the privatized response of the next user. We propose several utility functions related to well-known information metrics, such as (but not limited to) Fisher information matrix, total variation distance, and information entropy. We compare each of these utility metrics in terms of their computational complexity. We employ stochastic gradient Langevin dynamics for posterior sampling, a computationally efficient approximate Markov chain Monte Carlo method. We provide a theoretical analysis showing that (i) the posterior distribution targeted by the algorithm converges to the true parameter even for approximate posterior sampling, and (ii) the algorithm selects the optimal subset with high probability if posterior sampling is performed exactly. We also provide numerical results that empirically demonstrate the estimation accuracy of our algorithm where we compare it with nonadaptive and semi-adaptive approaches under experimental settings with various combinations of privacy parameters and population distribution parameters.

Statistic Selection and MCMC for Differentially Private Bayesian Estimation

This paper concerns differentially private Bayesian estimation of the parameters of a population distribution, when a statistic of a sample from that population is shared in noise to provide differential privacy. This work mainly addresses two problems: (1) What statistic of the sample should be shared privately? For the first question, i.e., the one about statistic selection, we promote using the Fisher information. We find out that, the statistic that is most informative in a non-privacy setting may not be the optimal choice under the privacy restrictions. We provide several examples to support that point. We consider several types of data sharing settings and propose several Monte Carlo-based numerical estimation methods for calculating the Fisher information for those settings. The second question concerns inference: (2) Based on the shared statistics, how could we perform effective Bayesian inference? We propose several Markov chain Monte Carlo (MCMC) algorithms for sampling from the posterior distribution of the parameter given the noisy statistic. The proposed MCMC algorithms can be preferred over one another depending on the problem. For example, when the shared statistics is additive and added Gaussian noise, a simple Metropolis-Hasting algorithm that utilizes the central limit theorem is a decent choice. We propose more advanced MCMC algorithms for several other cases of practical relevance. Our numerical examples involve comparing several candidate statistics to be shared privately. For each statistic, we perform Bayesian estimation based on the posterior distribution conditional on the privatized version of that statistic. We demonstrate that, the relative performance of a statistic, in terms of the mean squared error of the Bayesian estimator based on the corresponding privatized statistic, is adequately predicted by the Fisher information of the privatized statistic.

Learning with Subset Stacking

We propose a new algorithm that learns from a set of input-output pairs. Our algorithm is designed for populations where the relation between the input variables and the output variable exhibits a heterogeneous behavior across the predictor space. The algorithm starts with generating subsets that are concentrated around random points in the input space. This is followed by training a local predictor for each subset. Those predictors are then combined in a novel way to yield an overall predictor. We call this algorithm "LEarning with Subset Stacking" or LESS, due to its resemblance to method of stacking regressors. We compare the testing performance of LESS with the state-of-the-art methods on several datasets. Our comparison shows that LESS is a competitive supervised learning method. Moreover, we observe that LESS is also efficient in terms of computation time and it allows a straightforward parallel implementation.

Differentially Private Accelerated Optimization Algorithms

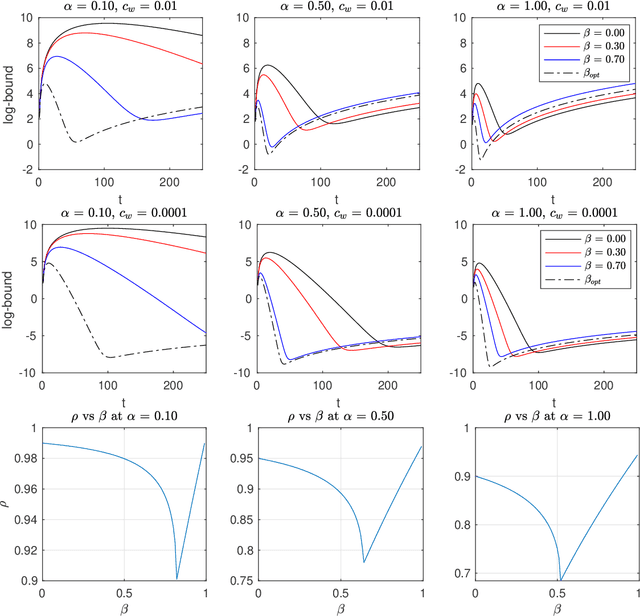
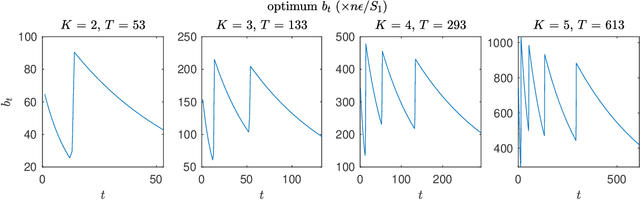
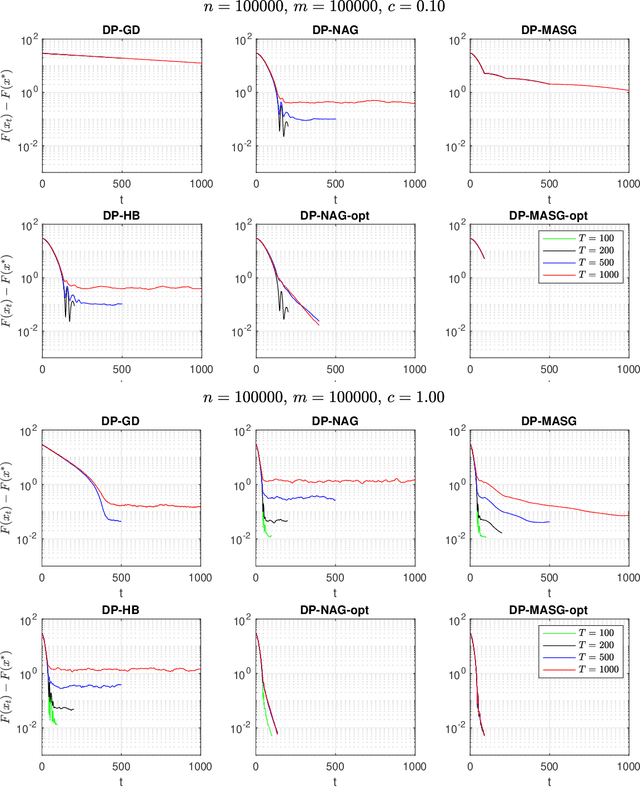
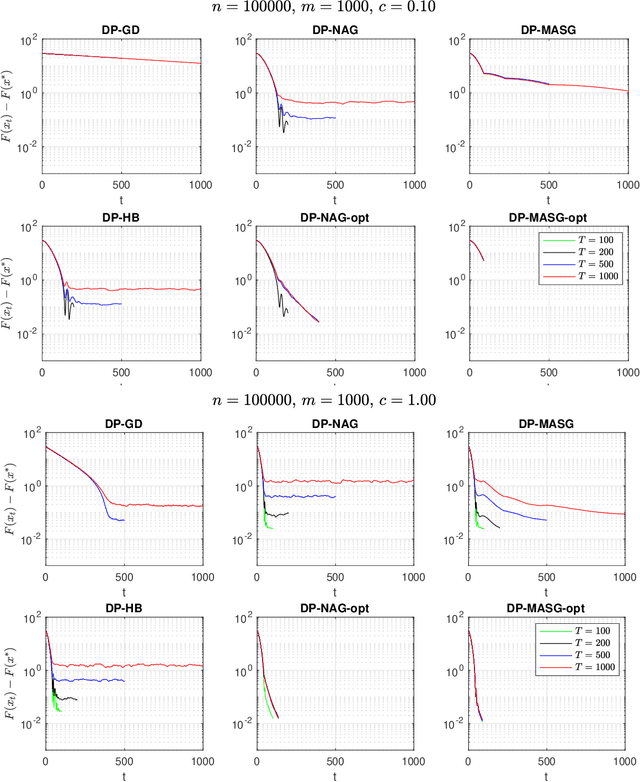
We present two classes of differentially private optimization algorithms derived from the well-known accelerated first-order methods. The first algorithm is inspired by Polyak's heavy ball method and employs a smoothing approach to decrease the accumulated noise on the gradient steps required for differential privacy. The second class of algorithms are based on Nesterov's accelerated gradient method and its recent multi-stage variant. We propose a noise dividing mechanism for the iterations of Nesterov's method in order to improve the error behavior of the algorithm. The convergence rate analyses are provided for both the heavy ball and the Nesterov's accelerated gradient method with the help of the dynamical system analysis techniques. Finally, we conclude with our numerical experiments showing that the presented algorithms have advantages over the well-known differentially private algorithms.

Bayesian Allocation Model: Inference by Sequential Monte Carlo for Nonnegative Tensor Factorizations and Topic Models using Polya Urns

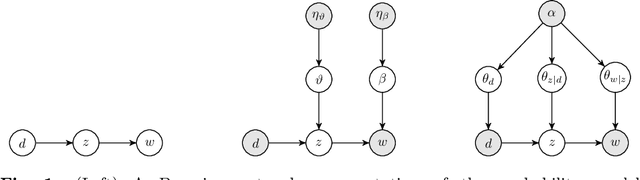
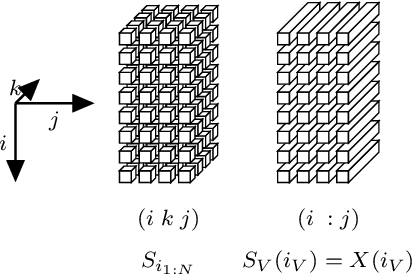
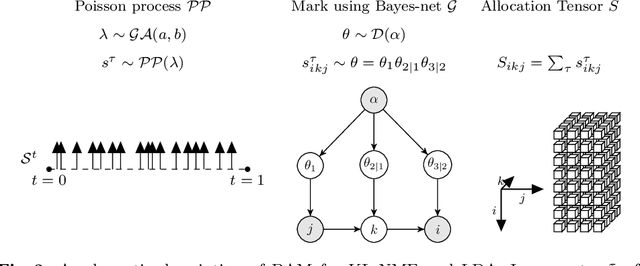
We introduce a dynamic generative model, Bayesian allocation model (BAM), which establishes explicit connections between nonnegative tensor factorization (NTF), graphical models of discrete probability distributions and their Bayesian extensions, and the topic models such as the latent Dirichlet allocation. BAM is based on a Poisson process, whose events are marked by using a Bayesian network, where the conditional probability tables of this network are then integrated out analytically. We show that the resulting marginal process turns out to be a Polya urn, an integer valued self-reinforcing process. This urn processes, which we name a Polya-Bayes process, obey certain conditional independence properties that provide further insight about the nature of NTF. These insights also let us develop space efficient simulation algorithms that respect the potential sparsity of data: we propose a class of sequential importance sampling algorithms for computing NTF and approximating their marginal likelihood, which would be useful for model selection. The resulting methods can also be viewed as a model scoring method for topic models and discrete Bayesian networks with hidden variables. The new algorithms have favourable properties in the sparse data regime when contrasted with variational algorithms that become more accurate when the total sum of the elements of the observed tensor goes to infinity. We illustrate the performance on several examples and numerically study the behaviour of the algorithms for various data regimes.

Image Segmentation with Pseudo-marginal MCMC Sampling and Nonparametric Shape Priors

In this paper, we propose an efficient pseudo-marginal Markov chain Monte Carlo (MCMC) sampling approach to draw samples from posterior shape distributions for image segmentation. The computation time of the proposed approach is independent from the size of the training set used to learn the shape prior distribution nonparametrically. Therefore, it scales well for very large data sets. Our approach is able to characterize the posterior probability density in the space of shapes through its samples, and to return multiple solutions, potentially from different modes of a multimodal probability density, which would be encountered, e.g., in segmenting objects from multiple shape classes. Experimental results demonstrate the potential of the proposed approach.

An Online Expectation-Maximisation Algorithm for Nonnegative Matrix Factorisation Models

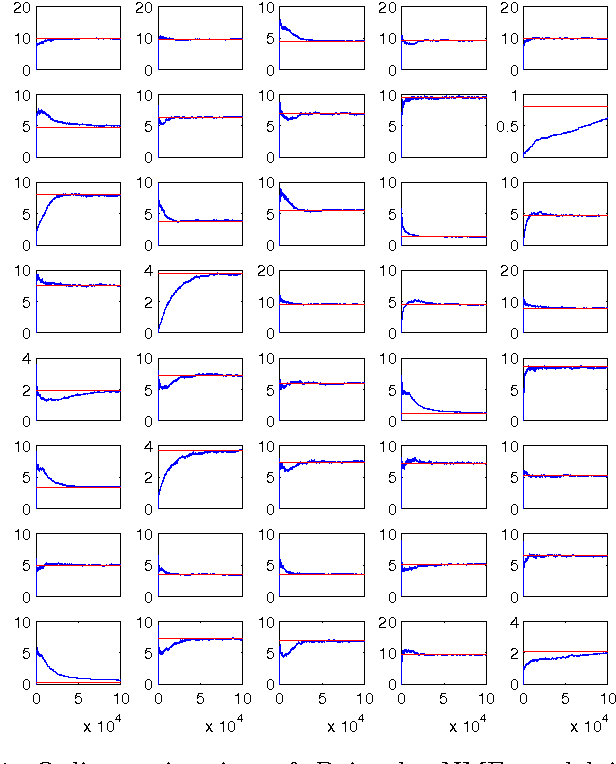
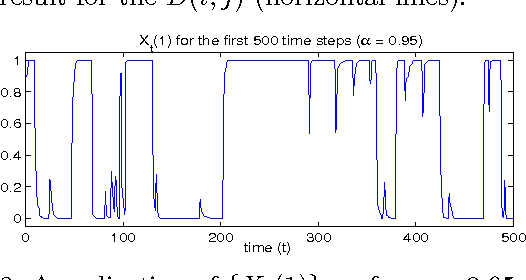
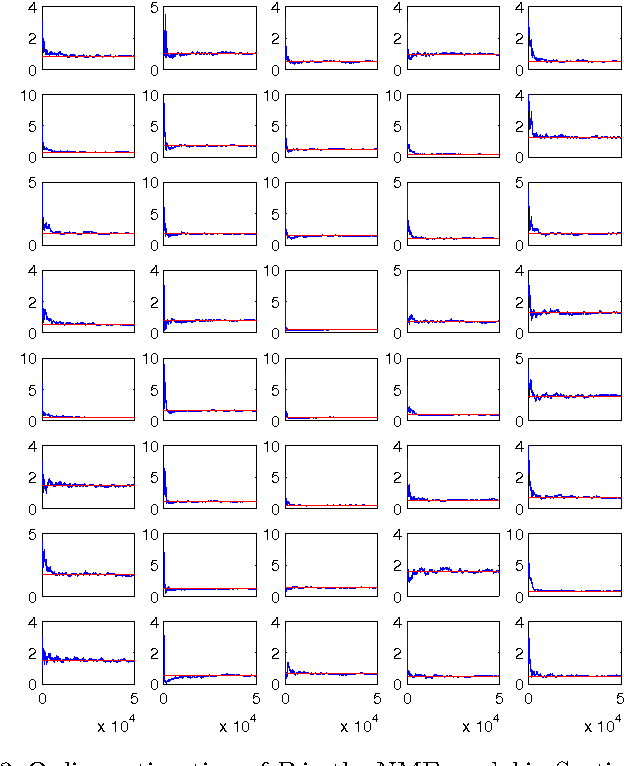
In this paper we formulate the nonnegative matrix factorisation (NMF) problem as a maximum likelihood estimation problem for hidden Markov models and propose online expectation-maximisation (EM) algorithms to estimate the NMF and the other unknown static parameters. We also propose a sequential Monte Carlo approximation of our online EM algorithm. We show the performance of the proposed method with two numerical examples.