Generating Multiple-Choice Knowledge Questions with Interpretable Difficulty Estimation using Knowledge Graphs and Large Language Models

Generating multiple-choice questions (MCQs) with difficulty estimation remains challenging in automated MCQ-generation systems used in adaptive, AI-assisted education. This study proposes a novel methodology for generating MCQs with difficulty estimation from the input documents by utilizing knowledge graphs (KGs) and large language models (LLMs). Our approach uses an LLM to construct a KG from input documents, from which MCQs are then systematically generated. Each MCQ is generated by selecting a node from the KG as the key, sampling a related triple or quintuple -- optionally augmented with an extra triple -- and prompting an LLM to generate a corresponding stem from these graph components. Distractors are then selected from the KG. For each MCQ, nine difficulty signals are computed and combined into a unified difficulty score using a data-driven approach. Experimental results demonstrate that our method generates high-quality MCQs whose difficulty estimation is interpretable and aligns with human perceptions. Our approach improves automated MCQ generation by integrating structured knowledge representations with LLMs and a data-driven difficulty estimation model.

MCMC for Bayesian estimation of Differential Privacy from Membership Inference Attacks

We propose a new framework for Bayesian estimation of differential privacy, incorporating evidence from multiple membership inference attacks (MIA). Bayesian estimation is carried out via a Markov chain Monte Carlo (MCMC) algorithm, named MCMC-DP-Est, which provides an estimate of the full posterior distribution of the privacy parameter (e.g., instead of just credible intervals). Critically, the proposed method does not assume that privacy auditing is performed with the most powerful attack on the worst-case (dataset, challenge point) pair, which is typically unrealistic. Instead, MCMC-DP-Est jointly estimates the strengths of MIAs used and the privacy of the training algorithm, yielding a more cautious privacy analysis. We also present an economical way to generate measurements for the performance of an MIA that is to be used by the MCMC method to estimate privacy. We present the use of the methods with numerical examples with both artificial and real data.

A Retrieval-Augmented Generation Framework for Academic Literature Navigation in Data Science

In the rapidly evolving field of data science, efficiently navigating the expansive body of academic literature is crucial for informed decision-making and innovation. This paper presents an enhanced Retrieval-Augmented Generation (RAG) application, an artificial intelligence (AI)-based system designed to assist data scientists in accessing precise and contextually relevant academic resources. The AI-powered application integrates advanced techniques, including the GeneRation Of BIbliographic Data (GROBID) technique for extracting bibliographic information, fine-tuned embedding models, semantic chunking, and an abstract-first retrieval method, to significantly improve the relevance and accuracy of the retrieved information. This implementation of AI specifically addresses the challenge of academic literature navigation. A comprehensive evaluation using the Retrieval-Augmented Generation Assessment System (RAGAS) framework demonstrates substantial improvements in key metrics, particularly Context Relevance, underscoring the system's effectiveness in reducing information overload and enhancing decision-making processes. Our findings highlight the potential of this enhanced Retrieval-Augmented Generation system to transform academic exploration within data science, ultimately advancing the workflow of research and innovation in the field.

Boosting Graph Embedding on a Single GPU

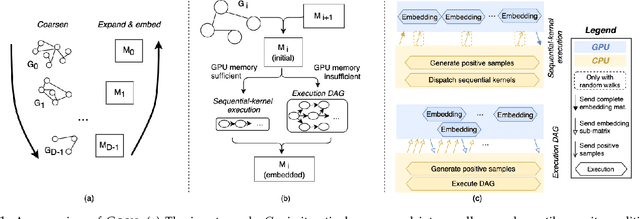
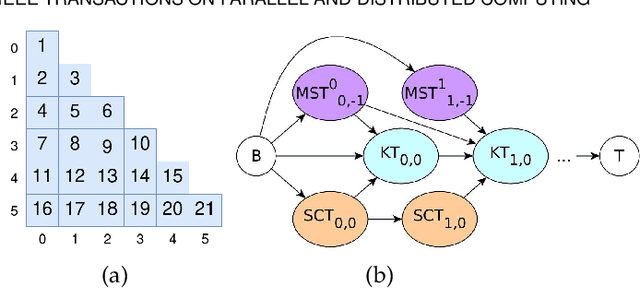
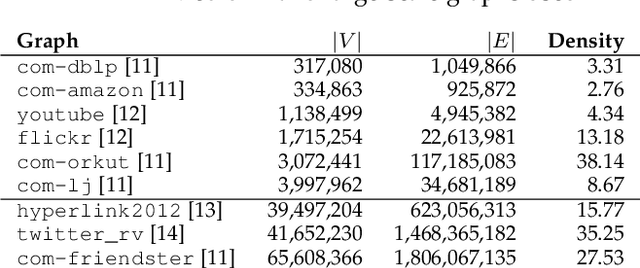
Graphs are ubiquitous, and they can model unique characteristics and complex relations of real-life systems. Although using machine learning (ML) on graphs is promising, their raw representation is not suitable for ML algorithms. Graph embedding represents each node of a graph as a d-dimensional vector which is more suitable for ML tasks. However, the embedding process is expensive, and CPU-based tools do not scale to real-world graphs. In this work, we present GOSH, a GPU-based tool for embedding large-scale graphs with minimum hardware constraints. GOSH employs a novel graph coarsening algorithm to enhance the impact of updates and minimize the work for embedding. It also incorporates a decomposition schema that enables any arbitrarily large graph to be embedded with a single GPU. As a result, GOSH sets a new state-of-the-art in link prediction both in accuracy and speed, and delivers high-quality embeddings for node classification at a fraction of the time compared to the state-of-the-art. For instance, it can embed a graph with over 65 million vertices and 1.8 billion edges in less than 30 minutes on a single GPU.

Understanding Coarsening for Embedding Large-Scale Graphs

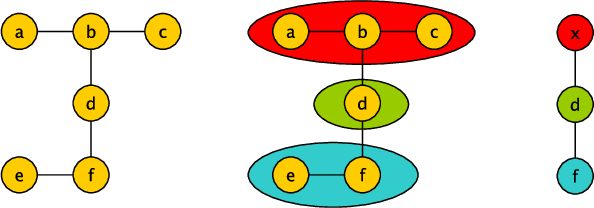
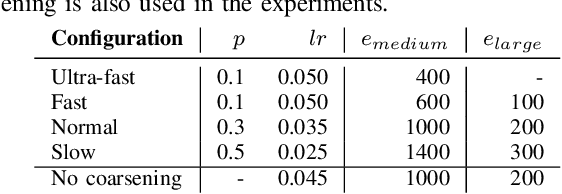
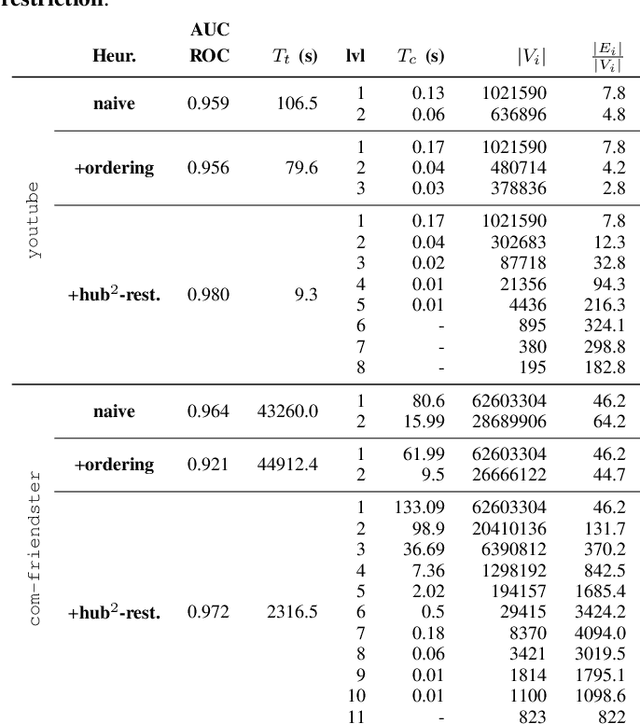
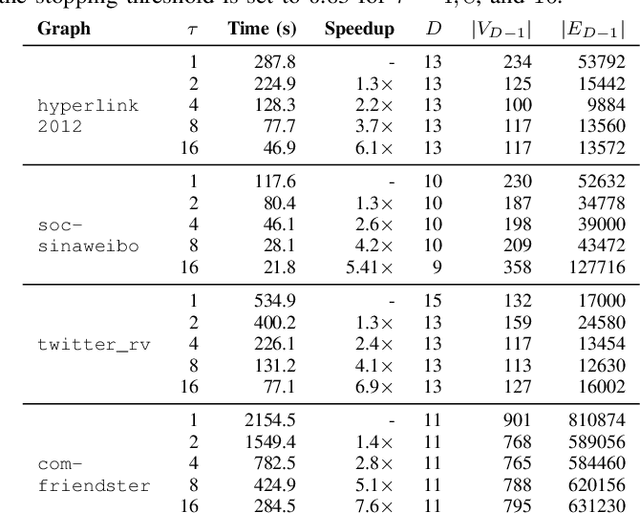
A significant portion of the data today, e.g, social networks, web connections, etc., can be modeled by graphs. A proper analysis of graphs with Machine Learning (ML) algorithms has the potential to yield far-reaching insights into many areas of research and industry. However, the irregular structure of graph data constitutes an obstacle for running ML tasks on graphs such as link prediction, node classification, and anomaly detection. Graph embedding is a compute-intensive process of representing graphs as a set of vectors in a d-dimensional space, which in turn makes it amenable to ML tasks. Many approaches have been proposed in the literature to improve the performance of graph embedding, e.g., using distributed algorithms, accelerators, and pre-processing techniques. Graph coarsening, which can be considered a pre-processing step, is a structural approximation of a given, large graph with a smaller one. As the literature suggests, the cost of embedding significantly decreases when coarsening is employed. In this work, we thoroughly analyze the impact of the coarsening quality on the embedding performance both in terms of speed and accuracy. Our experiments with a state-of-the-art, fast graph embedding tool show that there is an interplay between the coarsening decisions taken and the embedding quality.

HAMSI: A Parallel Incremental Optimization Algorithm Using Quadratic Approximations for Solving Partially Separable Problems

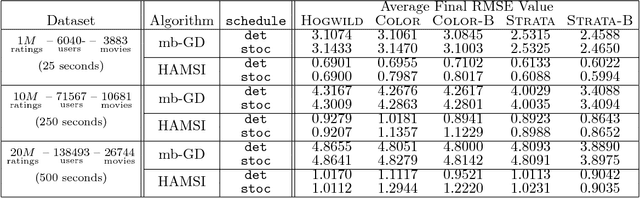
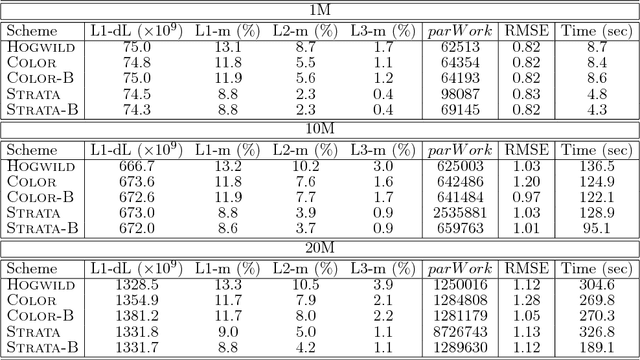
We propose HAMSI (Hessian Approximated Multiple Subsets Iteration), which is a provably convergent, second order incremental algorithm for solving large-scale partially separable optimization problems. The algorithm is based on a local quadratic approximation, and hence, allows incorporating curvature information to speed-up the convergence. HAMSI is inherently parallel and it scales nicely with the number of processors. Combined with techniques for effectively utilizing modern parallel computer architectures, we illustrate that the proposed method converges more rapidly than a parallel stochastic gradient descent when both methods are used to solve large-scale matrix factorization problems. This performance gain comes only at the expense of using memory that scales linearly with the total size of the optimization variables. We conclude that HAMSI may be considered as a viable alternative in many large scale problems, where first order methods based on variants of stochastic gradient descent are applicable.