An Indoor Localization Dataset and Data Collection Framework with High Precision Position Annotation

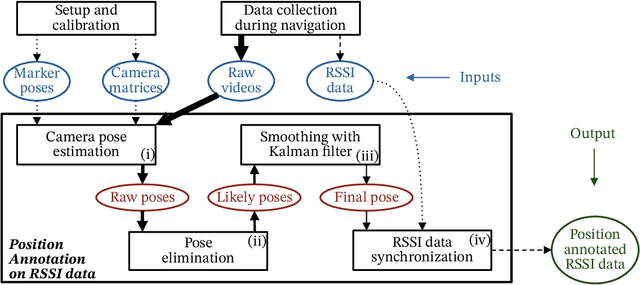
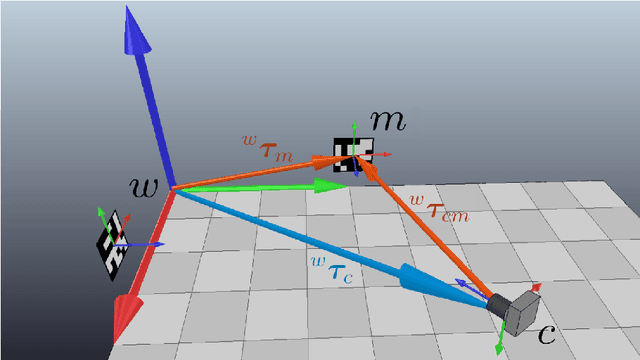
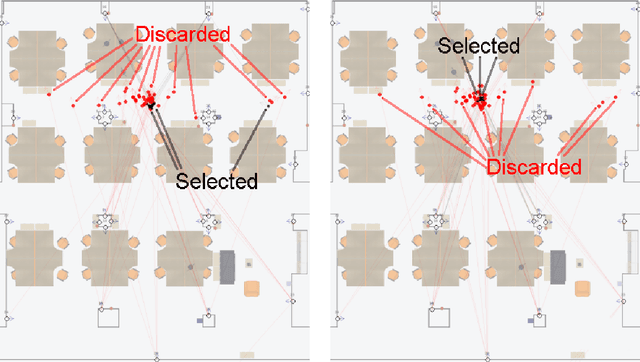
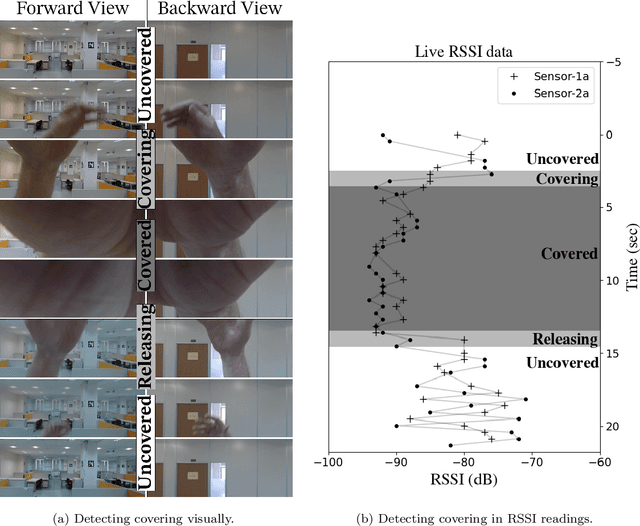
We introduce a novel technique and an associated high resolution dataset that aims to precisely evaluate wireless signal based indoor positioning algorithms. The technique implements an augmented reality (AR) based positioning system that is used to annotate the wireless signal parameter data samples with high precision position data. We track the position of a practical and low cost navigable setup of cameras and a Bluetooth Low Energy (BLE) beacon in an area decorated with AR markers. We maximize the performance of the AR-based localization by using a redundant number of markers. Video streams captured by the cameras are subjected to a series of marker recognition, subset selection and filtering operations to yield highly precise pose estimations. Our results show that we can reduce the positional error of the AR localization system to a rate under 0.05 meters. The position data are then used to annotate the BLE data that are captured simultaneously by the sensors stationed in the environment, hence, constructing a wireless signal data set with the ground truth, which allows a wireless signal based localization system to be evaluated accurately.

Autoencoding Variational Autoencoder

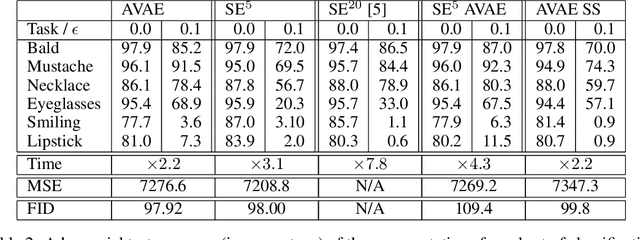
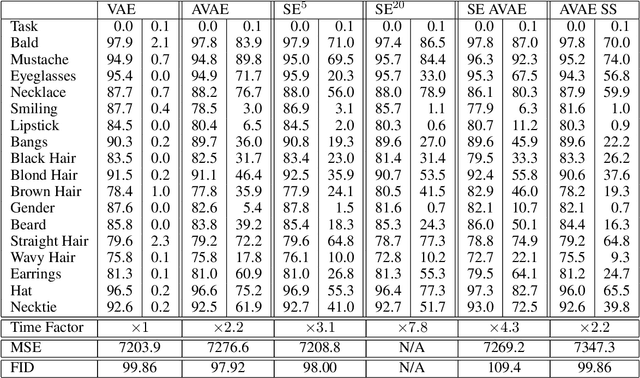
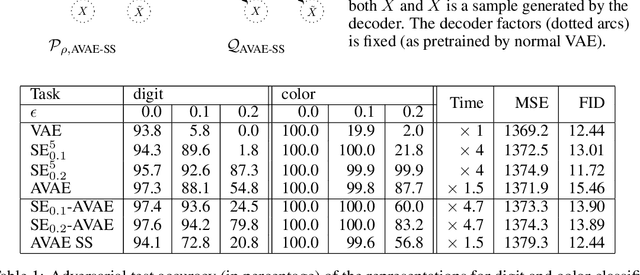
Does a Variational AutoEncoder (VAE) consistently encode typical samples generated from its decoder? This paper shows that the perhaps surprising answer to this question is `No'; a (nominally trained) VAE does not necessarily amortize inference for typical samples that it is capable of generating. We study the implications of this behaviour on the learned representations and also the consequences of fixing it by introducing a notion of self consistency. Our approach hinges on an alternative construction of the variational approximation distribution to the true posterior of an extended VAE model with a Markov chain alternating between the encoder and the decoder. The method can be used to train a VAE model from scratch or given an already trained VAE, it can be run as a post processing step in an entirely self supervised way without access to the original training data. Our experimental analysis reveals that encoders trained with our self-consistency approach lead to representations that are robust (insensitive) to perturbations in the input introduced by adversarial attacks. We provide experimental results on the ColorMnist and CelebA benchmark datasets that quantify the properties of the learned representations and compare the approach with a baseline that is specifically trained for the desired property.

Asynchronous Stochastic Quasi-Newton MCMC for Non-Convex Optimization

Recent studies have illustrated that stochastic gradient Markov Chain Monte Carlo techniques have a strong potential in non-convex optimization, where local and global convergence guarantees can be shown under certain conditions. By building up on this recent theory, in this study, we develop an asynchronous-parallel stochastic L-BFGS algorithm for non-convex optimization. The proposed algorithm is suitable for both distributed and shared-memory settings. We provide formal theoretical analysis and show that the proposed method achieves an ergodic convergence rate of ${\cal O}(1/\sqrt{N})$ ($N$ being the total number of iterations) and it can achieve a linear speedup under certain conditions. We perform several experiments on both synthetic and real datasets. The results support our theory and show that the proposed algorithm provides a significant speedup over the recently proposed synchronous distributed L-BFGS algorithm.

HAMSI: A Parallel Incremental Optimization Algorithm Using Quadratic Approximations for Solving Partially Separable Problems

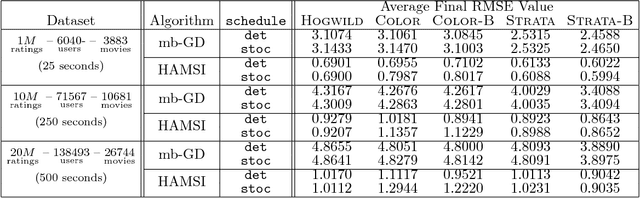
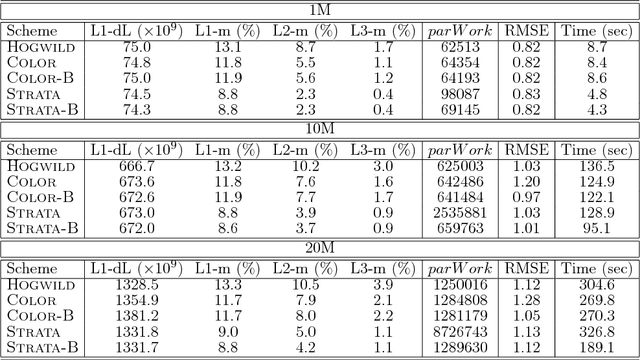
We propose HAMSI (Hessian Approximated Multiple Subsets Iteration), which is a provably convergent, second order incremental algorithm for solving large-scale partially separable optimization problems. The algorithm is based on a local quadratic approximation, and hence, allows incorporating curvature information to speed-up the convergence. HAMSI is inherently parallel and it scales nicely with the number of processors. Combined with techniques for effectively utilizing modern parallel computer architectures, we illustrate that the proposed method converges more rapidly than a parallel stochastic gradient descent when both methods are used to solve large-scale matrix factorization problems. This performance gain comes only at the expense of using memory that scales linearly with the total size of the optimization variables. We conclude that HAMSI may be considered as a viable alternative in many large scale problems, where first order methods based on variants of stochastic gradient descent are applicable.

Stochastic Quasi-Newton Langevin Monte Carlo

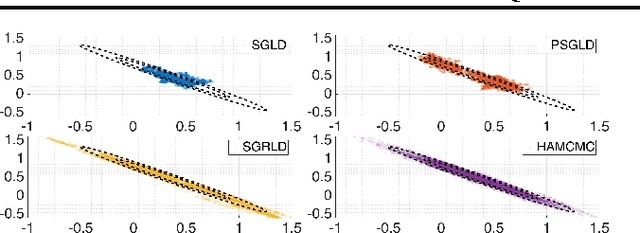
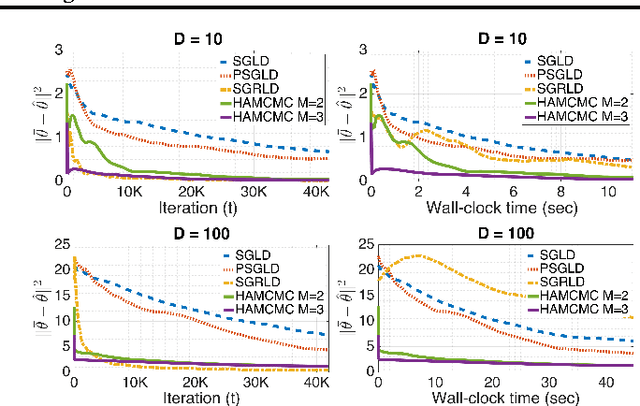
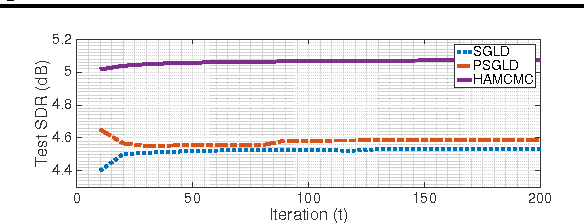
Recently, Stochastic Gradient Markov Chain Monte Carlo (SG-MCMC) methods have been proposed for scaling up Monte Carlo computations to large data problems. Whilst these approaches have proven useful in many applications, vanilla SG-MCMC might suffer from poor mixing rates when random variables exhibit strong couplings under the target densities or big scale differences. In this study, we propose a novel SG-MCMC method that takes the local geometry into account by using ideas from Quasi-Newton optimization methods. These second order methods directly approximate the inverse Hessian by using a limited history of samples and their gradients. Our method uses dense approximations of the inverse Hessian while keeping the time and memory complexities linear with the dimension of the problem. We provide a formal theoretical analysis where we show that the proposed method is asymptotically unbiased and consistent with the posterior expectations. We illustrate the effectiveness of the approach on both synthetic and real datasets. Our experiments on two challenging applications show that our method achieves fast convergence rates similar to Riemannian approaches while at the same time having low computational requirements similar to diagonal preconditioning approaches.

Parallel Stochastic Gradient Markov Chain Monte Carlo for Matrix Factorisation Models

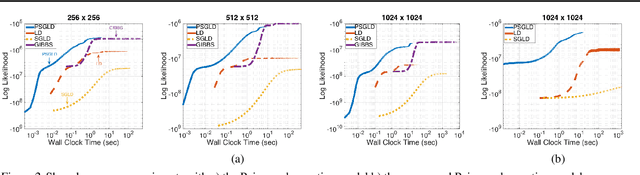
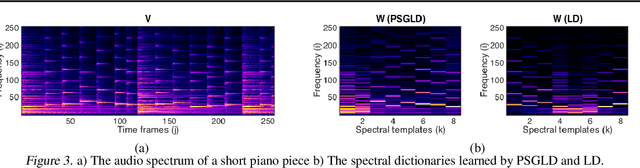
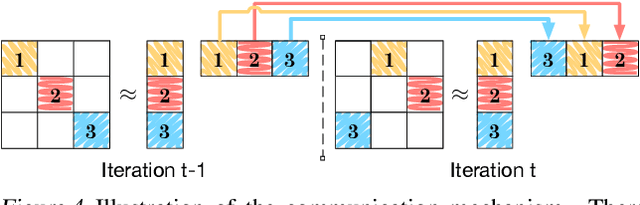
For large matrix factorisation problems, we develop a distributed Markov Chain Monte Carlo (MCMC) method based on stochastic gradient Langevin dynamics (SGLD) that we call Parallel SGLD (PSGLD). PSGLD has very favourable scaling properties with increasing data size and is comparable in terms of computational requirements to optimisation methods based on stochastic gradient descent. PSGLD achieves high performance by exploiting the conditional independence structure of the MF models to sub-sample data in a systematic manner as to allow parallelisation and distributed computation. We provide a convergence proof of the algorithm and verify its superior performance on various architectures such as Graphics Processing Units, shared memory multi-core systems and multi-computer clusters.

A Bayesian Tensor Factorization Model via Variational Inference for Link Prediction

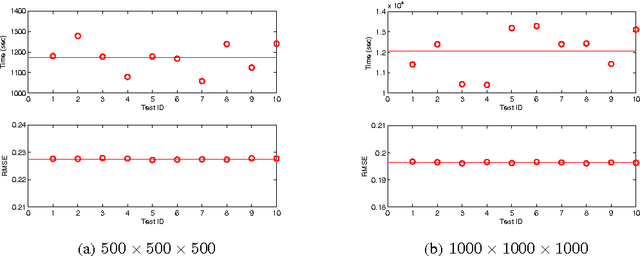
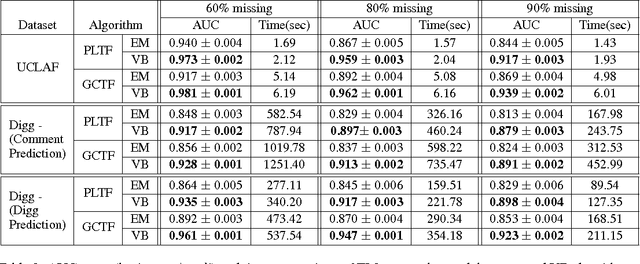
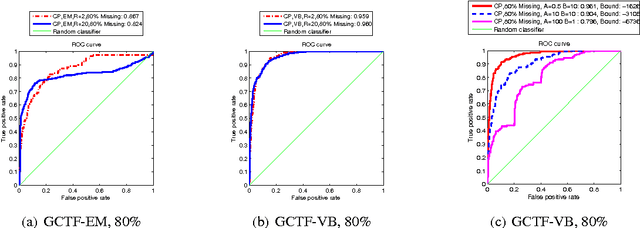
Probabilistic approaches for tensor factorization aim to extract meaningful structure from incomplete data by postulating low rank constraints. Recently, variational Bayesian (VB) inference techniques have successfully been applied to large scale models. This paper presents full Bayesian inference via VB on both single and coupled tensor factorization models. Our method can be run even for very large models and is easily implemented. It exhibits better prediction performance than existing approaches based on maximum likelihood on several real-world datasets for missing link prediction problem.

An Online Expectation-Maximisation Algorithm for Nonnegative Matrix Factorisation Models

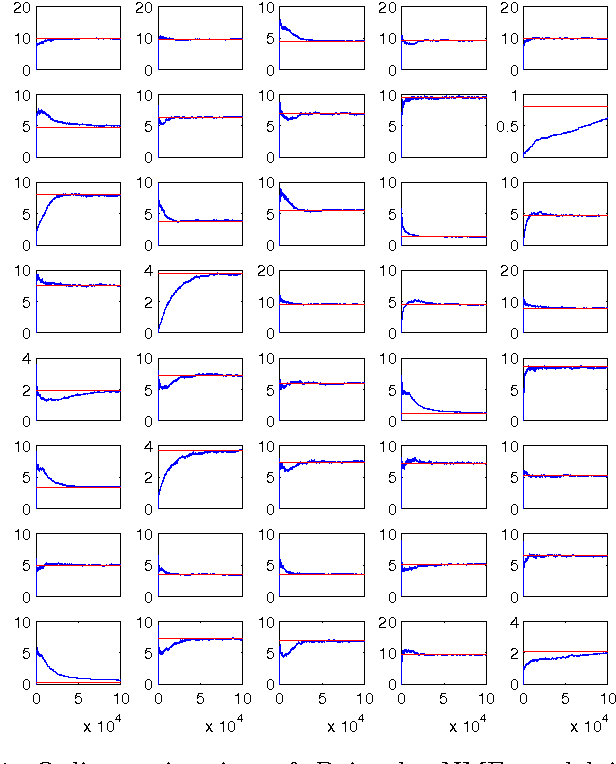
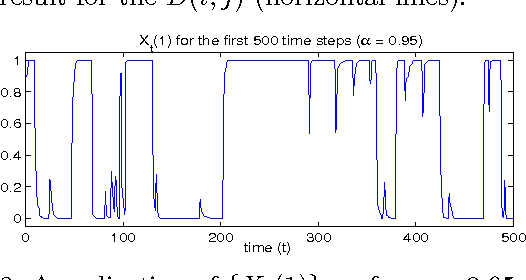
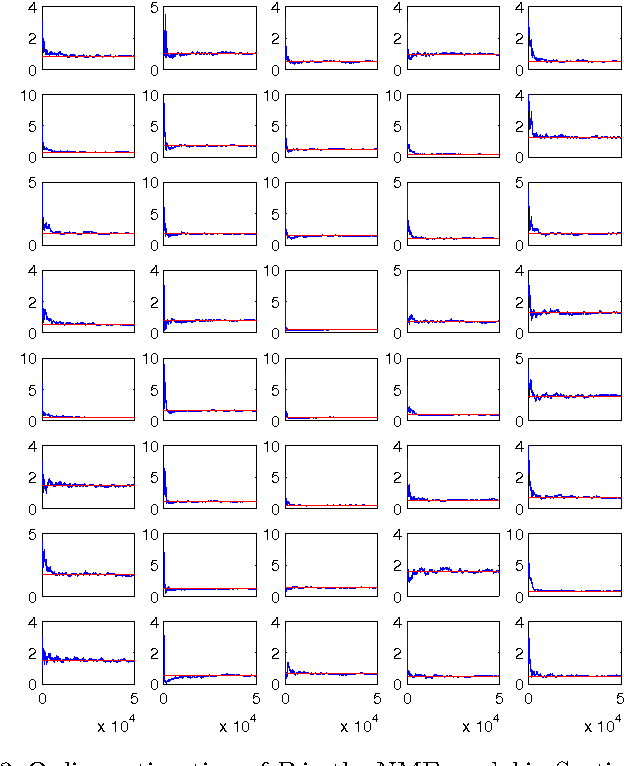
In this paper we formulate the nonnegative matrix factorisation (NMF) problem as a maximum likelihood estimation problem for hidden Markov models and propose online expectation-maximisation (EM) algorithms to estimate the NMF and the other unknown static parameters. We also propose a sequential Monte Carlo approximation of our online EM algorithm. We show the performance of the proposed method with two numerical examples.

Alpha/Beta Divergences and Tweedie Models

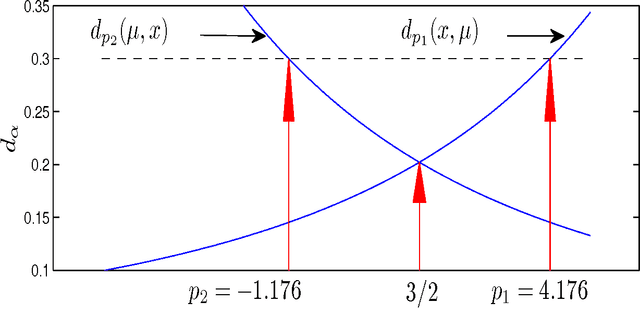
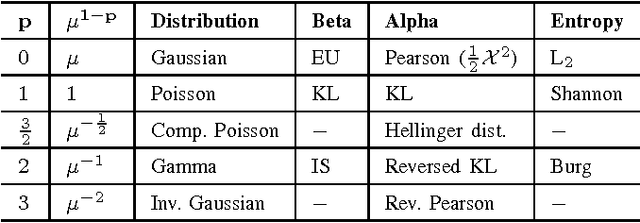
We describe the underlying probabilistic interpretation of alpha and beta divergences. We first show that beta divergences are inherently tied to Tweedie distributions, a particular type of exponential family, known as exponential dispersion models. Starting from the variance function of a Tweedie model, we outline how to get alpha and beta divergences as special cases of Csisz\'ar's $f$ and Bregman divergences. This result directly generalizes the well-known relationship between the Gaussian distribution and least squares estimation to Tweedie models and beta divergence minimization.

Link Prediction via Generalized Coupled Tensor Factorisation

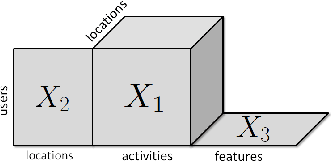
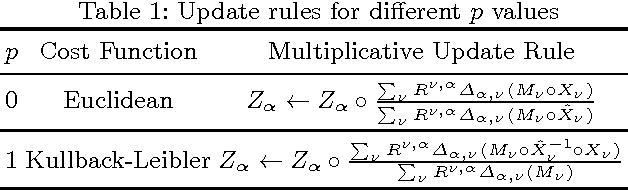
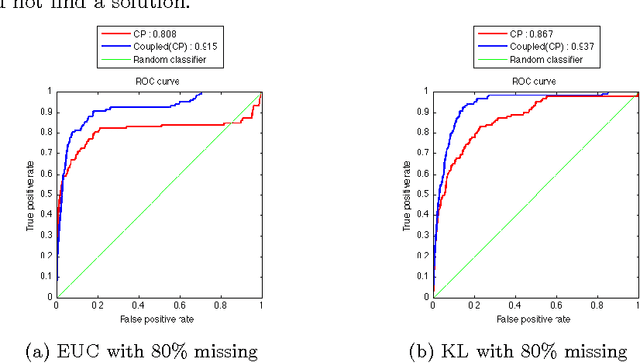
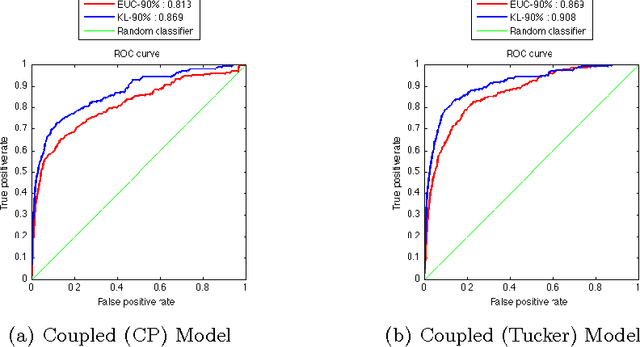
This study deals with the missing link prediction problem: the problem of predicting the existence of missing connections between entities of interest. We address link prediction using coupled analysis of relational datasets represented as heterogeneous data, i.e., datasets in the form of matrices and higher-order tensors. We propose to use an approach based on probabilistic interpretation of tensor factorisation models, i.e., Generalised Coupled Tensor Factorisation, which can simultaneously fit a large class of tensor models to higher-order tensors/matrices with com- mon latent factors using different loss functions. Numerical experiments demonstrate that joint analysis of data from multiple sources via coupled factorisation improves the link prediction performance and the selection of right loss function and tensor model is crucial for accurately predicting missing links.