HAMSI: A Parallel Incremental Optimization Algorithm Using Quadratic Approximations for Solving Partially Separable Problems

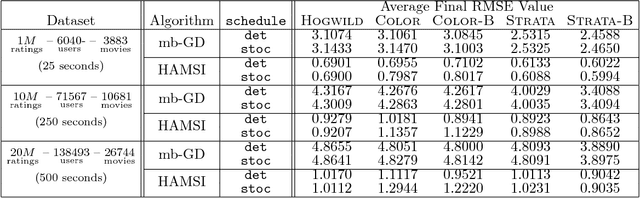
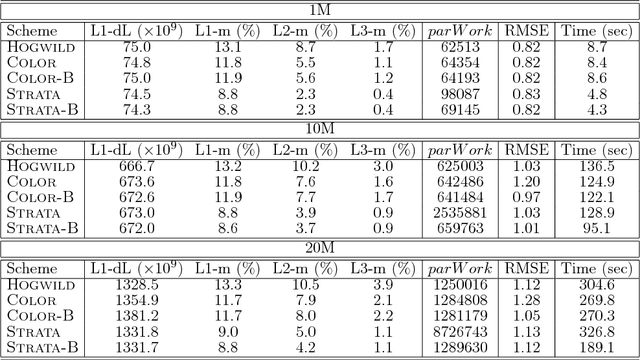
We propose HAMSI (Hessian Approximated Multiple Subsets Iteration), which is a provably convergent, second order incremental algorithm for solving large-scale partially separable optimization problems. The algorithm is based on a local quadratic approximation, and hence, allows incorporating curvature information to speed-up the convergence. HAMSI is inherently parallel and it scales nicely with the number of processors. Combined with techniques for effectively utilizing modern parallel computer architectures, we illustrate that the proposed method converges more rapidly than a parallel stochastic gradient descent when both methods are used to solve large-scale matrix factorization problems. This performance gain comes only at the expense of using memory that scales linearly with the total size of the optimization variables. We conclude that HAMSI may be considered as a viable alternative in many large scale problems, where first order methods based on variants of stochastic gradient descent are applicable.

Parallel Stochastic Gradient Markov Chain Monte Carlo for Matrix Factorisation Models

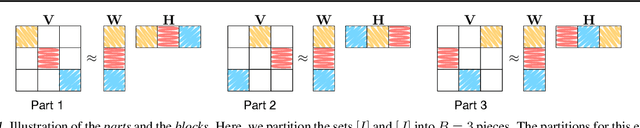
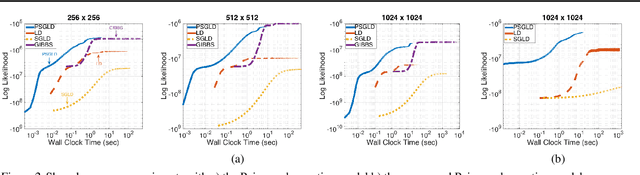
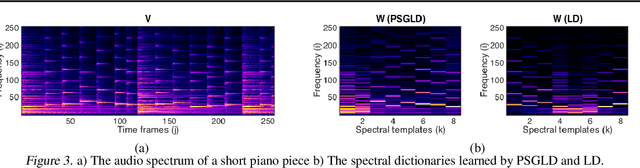
For large matrix factorisation problems, we develop a distributed Markov Chain Monte Carlo (MCMC) method based on stochastic gradient Langevin dynamics (SGLD) that we call Parallel SGLD (PSGLD). PSGLD has very favourable scaling properties with increasing data size and is comparable in terms of computational requirements to optimisation methods based on stochastic gradient descent. PSGLD achieves high performance by exploiting the conditional independence structure of the MF models to sub-sample data in a systematic manner as to allow parallelisation and distributed computation. We provide a convergence proof of the algorithm and verify its superior performance on various architectures such as Graphics Processing Units, shared memory multi-core systems and multi-computer clusters.