Counterfactual Explanations for Linear Optimization

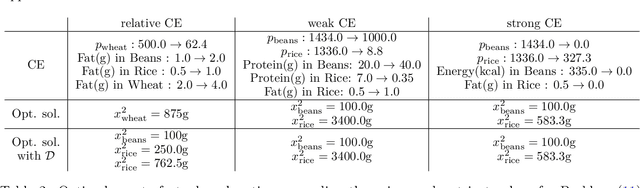
The concept of counterfactual explanations (CE) has emerged as one of the important concepts to understand the inner workings of complex AI systems. In this paper, we translate the idea of CEs to linear optimization and propose, motivate, and analyze three different types of CEs: strong, weak, and relative. While deriving strong and weak CEs appears to be computationally intractable, we show that calculating relative CEs can be done efficiently. By detecting and exploiting the hidden convex structure of the optimization problem that arises in the latter case, we show that obtaining relative CEs can be done in the same magnitude of time as solving the original linear optimization problem. This is confirmed by an extensive numerical experiment study on the NETLIB library.

Output-Constrained Decision Trees

When there is a correlation between any pair of targets, one needs a prediction method that can handle vector-valued output. In this setting, multi-target learning is particularly important as it is widely used in various applications. This paper introduces new variants of decision trees that can handle not only multi-target output but also the constraints among the targets. We focus on the customization of conventional decision trees by adjusting the splitting criteria to handle the constraints and obtain feasible predictions. We present both an optimization-based exact approach and several heuristics, complete with a discussion on their respective advantages and disadvantages. To support our findings, we conduct a computational study to demonstrate and compare the results of the proposed approaches.

Fixing confirmation bias in feature attribution methods via semantic match

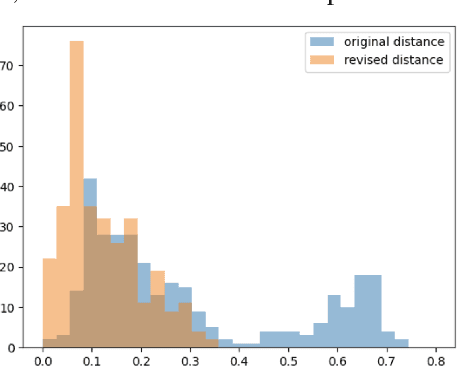
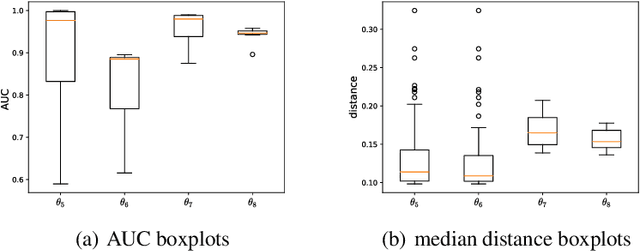
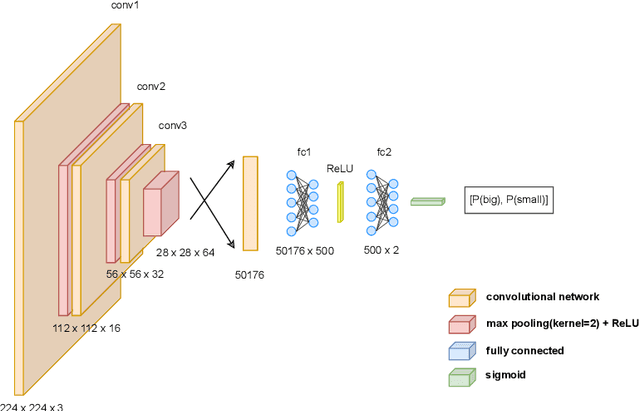
Feature attribution methods have become a staple method to disentangle the complex behavior of black box models. Despite their success, some scholars have argued that such methods suffer from a serious flaw: they do not allow a reliable interpretation in terms of human concepts. Simply put, visualizing an array of feature contributions is not enough for humans to conclude something about a model's internal representations, and confirmation bias can trick users into false beliefs about model behavior. We argue that a structured approach is required to test whether our hypotheses on the model are confirmed by the feature attributions. This is what we call the "semantic match" between human concepts and (sub-symbolic) explanations. Building on the conceptual framework put forward in Cin\`a et al. [2023], we propose a structured approach to evaluate semantic match in practice. We showcase the procedure in a suite of experiments spanning tabular and image data, and show how the assessment of semantic match can give insight into both desirable (e.g., focusing on an object relevant for prediction) and undesirable model behaviors (e.g., focusing on a spurious correlation). We couple our experimental results with an analysis on the metrics to measure semantic match, and argue that this approach constitutes the first step towards resolving the issue of confirmation bias in XAI.

Differentially Private Distributed Bayesian Linear Regression with MCMC

We propose a novel Bayesian inference framework for distributed differentially private linear regression. We consider a distributed setting where multiple parties hold parts of the data and share certain summary statistics of their portions in privacy-preserving noise. We develop a novel generative statistical model for privately shared statistics, which exploits a useful distributional relation between the summary statistics of linear regression. Bayesian estimation of the regression coefficients is conducted mainly using Markov chain Monte Carlo algorithms, while we also provide a fast version to perform Bayesian estimation in one iteration. The proposed methods have computational advantages over their competitors. We provide numerical results on both real and simulated data, which demonstrate that the proposed algorithms provide well-rounded estimation and prediction.

Semantic match: Debugging feature attribution methods in XAI for healthcare

The recent spike in certified Artificial Intelligence (AI) tools for healthcare has renewed the debate around adoption of this technology. One thread of such debate concerns Explainable AI (XAI) and its promise to render AI devices more transparent and trustworthy. A few voices active in the medical AI space have expressed concerns on the reliability of Explainable AI techniques and especially feature attribution methods, questioning their use and inclusion in guidelines and standards. Despite valid concerns, we argue that existing criticism on the viability of post-hoc local explainability methods throws away the baby with the bathwater by generalizing a problem that is specific to image data. We begin by characterizing the problem as a lack of semantic match between explanations and human understanding. To understand when feature importance can be used reliably, we introduce a distinction between feature importance of low- and high-level features. We argue that for data types where low-level features come endowed with a clear semantics, such as tabular data like Electronic Health Records (EHRs), semantic match can be obtained, and thus feature attribution methods can still be employed in a meaningful and useful way.

Discovering Classification Rules for Interpretable Learning with Linear Programming

Rules embody a set of if-then statements which include one or more conditions to classify a subset of samples in a dataset. In various applications such classification rules are considered to be interpretable by the decision makers. We introduce two new algorithms for interpretability and learning. Both algorithms take advantage of linear programming, and hence, they are scalable to large data sets. The first algorithm extracts rules for interpretation of trained models that are based on tree/rule ensembles. The second algorithm generates a set of classification rules through a column generation approach. The proposed algorithms return a set of rules along with their optimal weights indicating the importance of each rule for classification. Moreover, our algorithms allow assigning cost coefficients, which could relate to different attributes of the rules, such as; rule lengths, estimator weights, number of false negatives, and so on. Thus, the decision makers can adjust these coefficients to divert the training process and obtain a set of rules that are more appealing for their needs. We have tested the performances of both algorithms on a collection of datasets and presented a case study to elaborate on optimal rule weights. Our results show that a good compromise between interpretability and accuracy can be obtained by the proposed algorithms.

Differentially Private Accelerated Optimization Algorithms

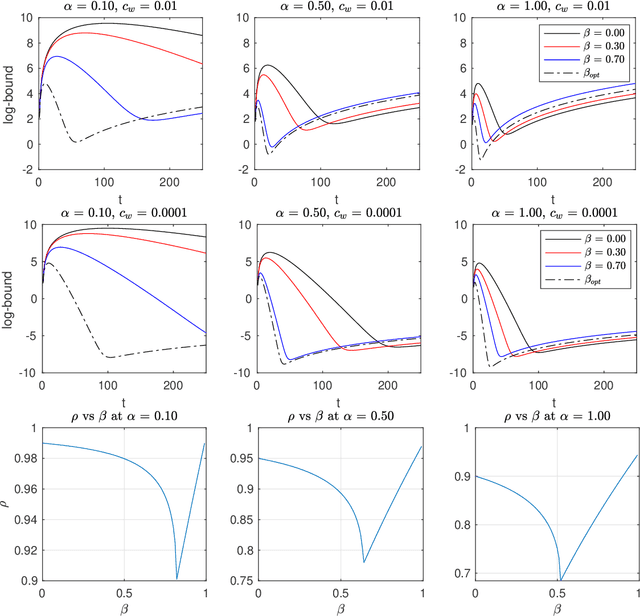
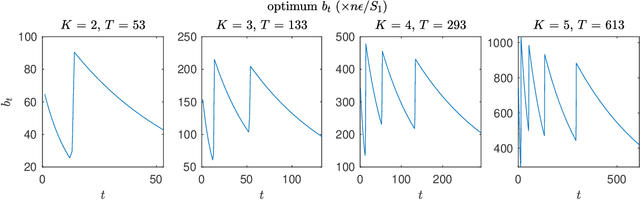
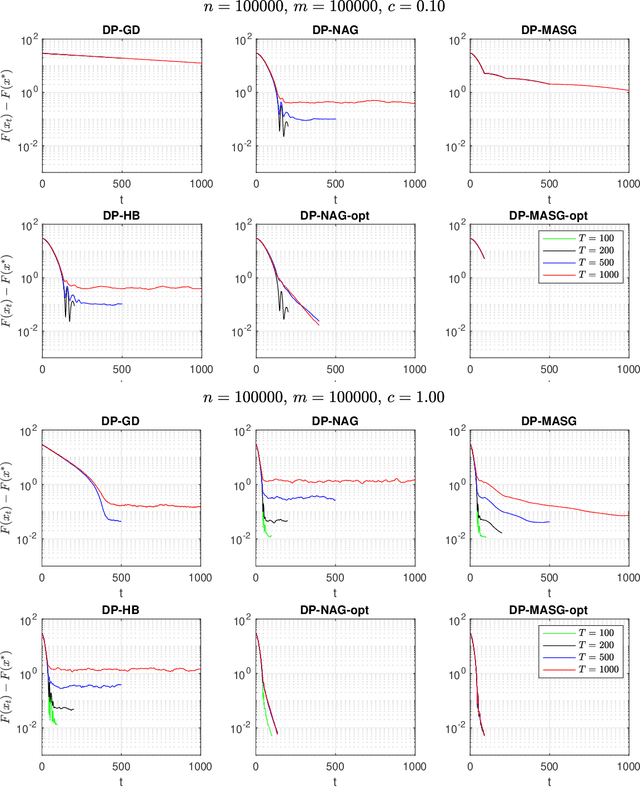
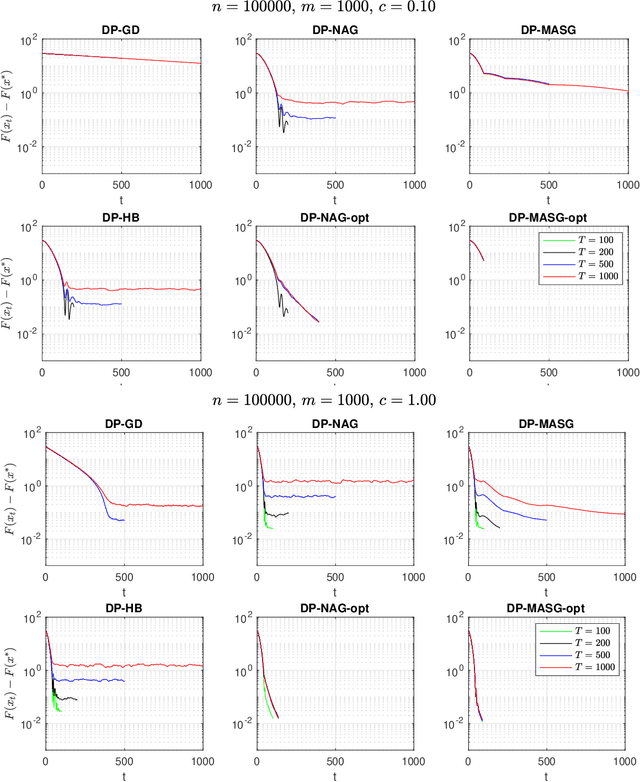
We present two classes of differentially private optimization algorithms derived from the well-known accelerated first-order methods. The first algorithm is inspired by Polyak's heavy ball method and employs a smoothing approach to decrease the accumulated noise on the gradient steps required for differential privacy. The second class of algorithms are based on Nesterov's accelerated gradient method and its recent multi-stage variant. We propose a noise dividing mechanism for the iterations of Nesterov's method in order to improve the error behavior of the algorithm. The convergence rate analyses are provided for both the heavy ball and the Nesterov's accelerated gradient method with the help of the dynamical system analysis techniques. Finally, we conclude with our numerical experiments showing that the presented algorithms have advantages over the well-known differentially private algorithms.

HAMSI: A Parallel Incremental Optimization Algorithm Using Quadratic Approximations for Solving Partially Separable Problems

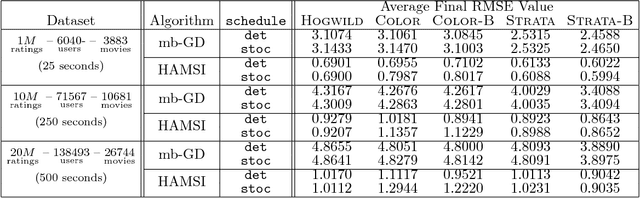
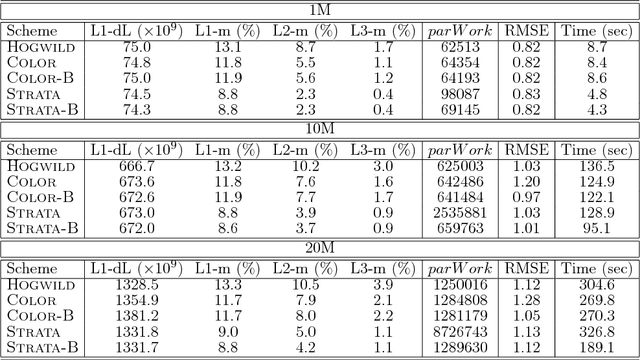
We propose HAMSI (Hessian Approximated Multiple Subsets Iteration), which is a provably convergent, second order incremental algorithm for solving large-scale partially separable optimization problems. The algorithm is based on a local quadratic approximation, and hence, allows incorporating curvature information to speed-up the convergence. HAMSI is inherently parallel and it scales nicely with the number of processors. Combined with techniques for effectively utilizing modern parallel computer architectures, we illustrate that the proposed method converges more rapidly than a parallel stochastic gradient descent when both methods are used to solve large-scale matrix factorization problems. This performance gain comes only at the expense of using memory that scales linearly with the total size of the optimization variables. We conclude that HAMSI may be considered as a viable alternative in many large scale problems, where first order methods based on variants of stochastic gradient descent are applicable.

Parallel Stochastic Gradient Markov Chain Monte Carlo for Matrix Factorisation Models

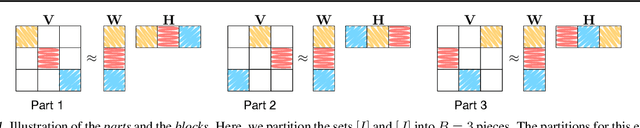
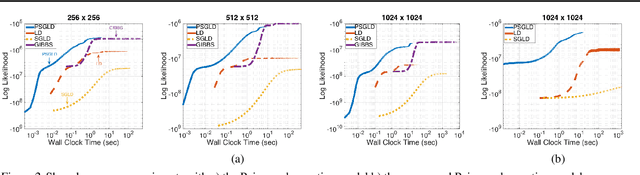
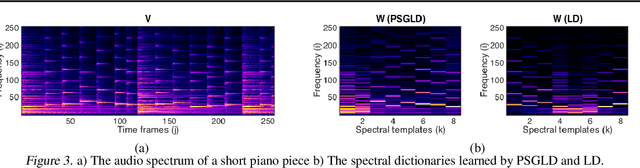
For large matrix factorisation problems, we develop a distributed Markov Chain Monte Carlo (MCMC) method based on stochastic gradient Langevin dynamics (SGLD) that we call Parallel SGLD (PSGLD). PSGLD has very favourable scaling properties with increasing data size and is comparable in terms of computational requirements to optimisation methods based on stochastic gradient descent. PSGLD achieves high performance by exploiting the conditional independence structure of the MF models to sub-sample data in a systematic manner as to allow parallelisation and distributed computation. We provide a convergence proof of the algorithm and verify its superior performance on various architectures such as Graphics Processing Units, shared memory multi-core systems and multi-computer clusters.