Counterfactual Explanations for Linear Optimization

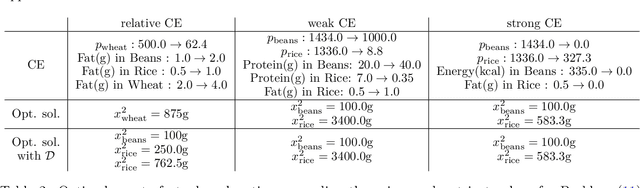
The concept of counterfactual explanations (CE) has emerged as one of the important concepts to understand the inner workings of complex AI systems. In this paper, we translate the idea of CEs to linear optimization and propose, motivate, and analyze three different types of CEs: strong, weak, and relative. While deriving strong and weak CEs appears to be computationally intractable, we show that calculating relative CEs can be done efficiently. By detecting and exploiting the hidden convex structure of the optimization problem that arises in the latter case, we show that obtaining relative CEs can be done in the same magnitude of time as solving the original linear optimization problem. This is confirmed by an extensive numerical experiment study on the NETLIB library.

From Large Language Models and Optimization to Decision Optimization CoPilot: A Research Manifesto

Significantly simplifying the creation of optimization models for real-world business problems has long been a major goal in applying mathematical optimization more widely to important business and societal decisions. The recent capabilities of Large Language Models (LLMs) present a timely opportunity to achieve this goal. Therefore, we propose research at the intersection of LLMs and optimization to create a Decision Optimization CoPilot (DOCP) - an AI tool designed to assist any decision maker, interacting in natural language to grasp the business problem, subsequently formulating and solving the corresponding optimization model. This paper outlines our DOCP vision and identifies several fundamental requirements for its implementation. We describe the state of the art through a literature survey and experiments using ChatGPT. We show that a) LLMs already provide substantial novel capabilities relevant to a DOCP, and b) major research challenges remain to be addressed. We also propose possible research directions to overcome these gaps. We also see this work as a call to action to bring together the LLM and optimization communities to pursue our vision, thereby enabling much more widespread improved decision-making.

Finding Regions of Counterfactual Explanations via Robust Optimization

Counterfactual explanations play an important role in detecting bias and improving the explainability of data-driven classification models. A counterfactual explanation (CE) is a minimal perturbed data point for which the decision of the model changes. Most of the existing methods can only provide one CE, which may not be achievable for the user. In this work we derive an iterative method to calculate robust CEs, i.e. CEs that remain valid even after the features are slightly perturbed. To this end, our method provides a whole region of CEs allowing the user to choose a suitable recourse to obtain a desired outcome. We use algorithmic ideas from robust optimization and prove convergence results for the most common machine learning methods including logistic regression, decision trees, random forests, and neural networks. Our experiments show that our method can efficiently generate globally optimal robust CEs for a variety of common data sets and classification models.

A Robust Optimization Approach to Deep Learning

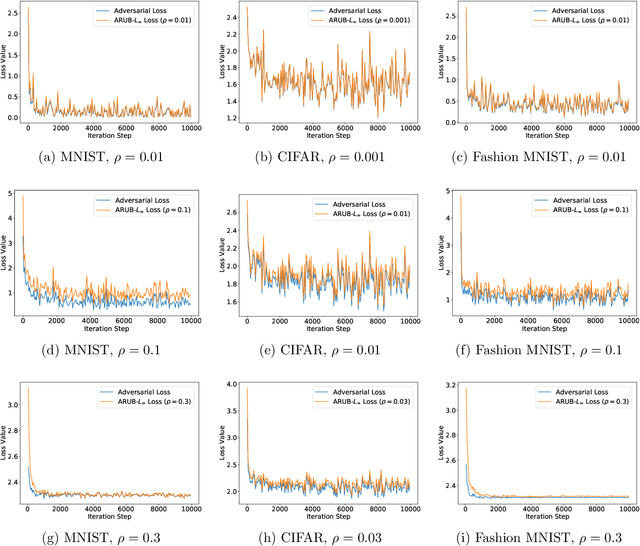
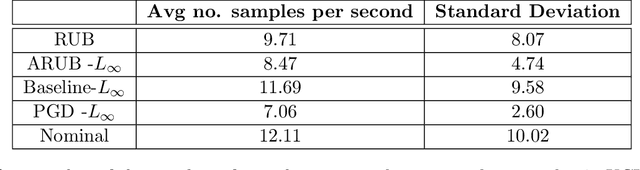
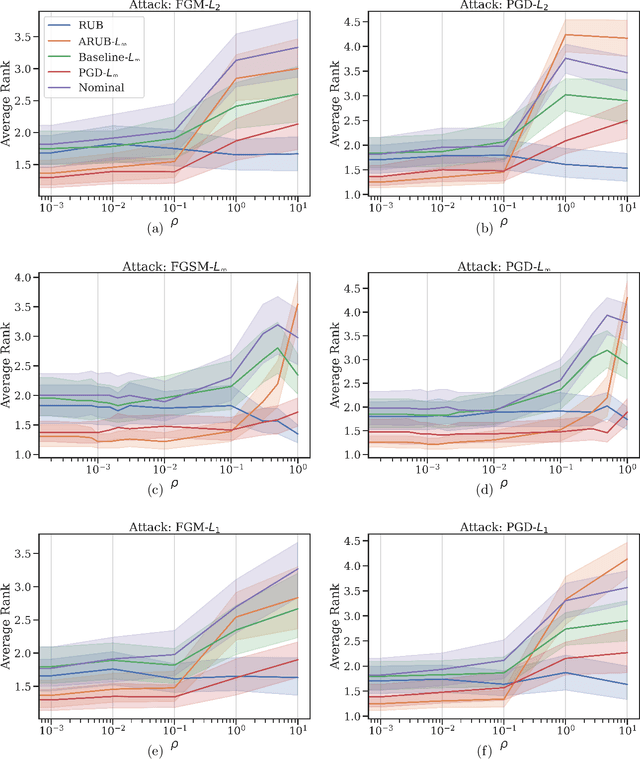
Many state-of-the-art adversarial training methods leverage upper bounds of the adversarial loss to provide security guarantees. Yet, these methods require computations at each training step that can not be incorporated in the gradient for backpropagation. We introduce a new, more principled approach to adversarial training based on a closed form solution of an upper bound of the adversarial loss, which can be effectively trained with backpropagation. This bound is facilitated by state-of-the-art tools from robust optimization. We derive two new methods with our approach. The first method (Approximated Robust Upper Bound or aRUB) uses the first order approximation of the network as well as basic tools from linear robust optimization to obtain an approximate upper bound of the adversarial loss that can be easily implemented. The second method (Robust Upper Bound or RUB), computes an exact upper bound of the adversarial loss. Across a variety of tabular and vision data sets we demonstrate the effectiveness of our more principled approach -- RUB is substantially more robust than state-of-the-art methods for larger perturbations, while aRUB matches the performance of state-of-the-art methods for small perturbations. Also, both RUB and aRUB run faster than standard adversarial training (at the expense of an increase in memory). All the code to reproduce the results can be found at https://github.com/kimvc7/Robustness.

Mixed-Integer Optimization with Constraint Learning

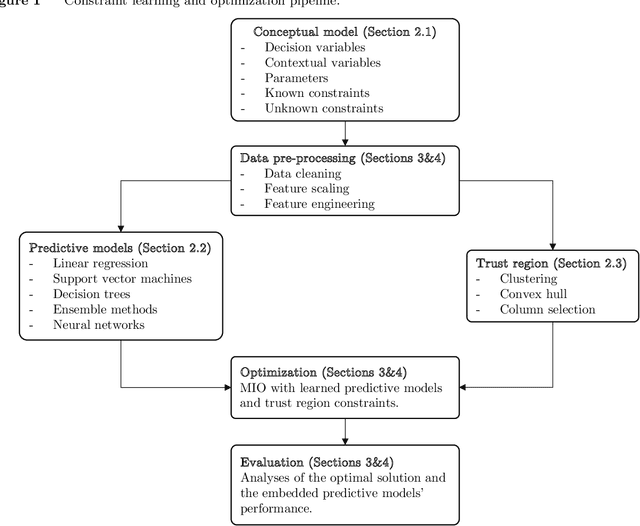
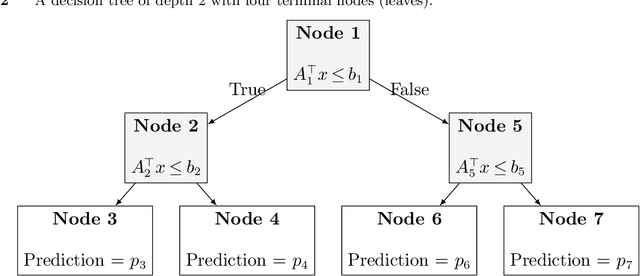
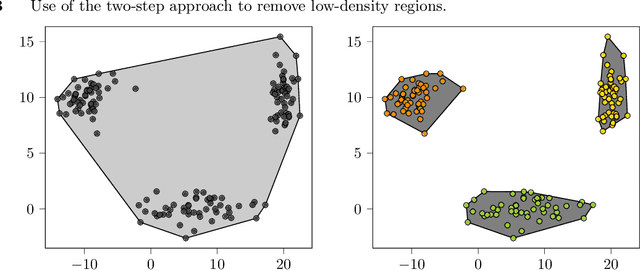
We establish a broad methodological foundation for mixed-integer optimization with learned constraints. We propose an end-to-end pipeline for data-driven decision making in which constraints and objectives are directly learned from data using machine learning, and the trained models are embedded in an optimization formulation. We exploit the mixed-integer optimization-representability of many machine learning methods, including linear models, decision trees, ensembles, and multi-layer perceptrons. The consideration of multiple methods allows us to capture various underlying relationships between decisions, contextual variables, and outcomes. We also characterize a decision trust region using the convex hull of the observations, to ensure credible recommendations and avoid extrapolation. We efficiently incorporate this representation using column generation and clustering. In combination with domain-driven constraints and objective terms, the embedded models and trust region define a mixed-integer optimization problem for prescription generation. We implement this framework as a Python package (OptiCL) for practitioners. We demonstrate the method in both chemotherapy optimization and World Food Programme planning. The case studies illustrate the benefit of the framework in generating high-quality prescriptions, the value added by the trust region, the incorporation of multiple machine learning methods, and the inclusion of multiple learned constraints.

Optimization with Constraint Learning: A Framework and Survey

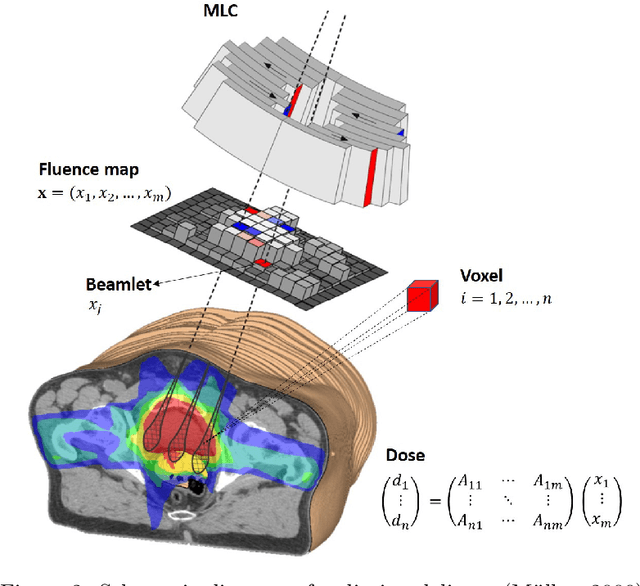
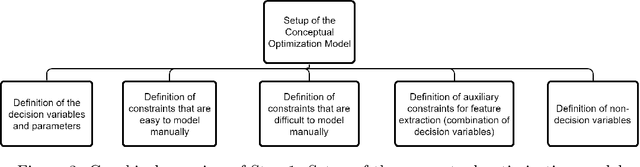
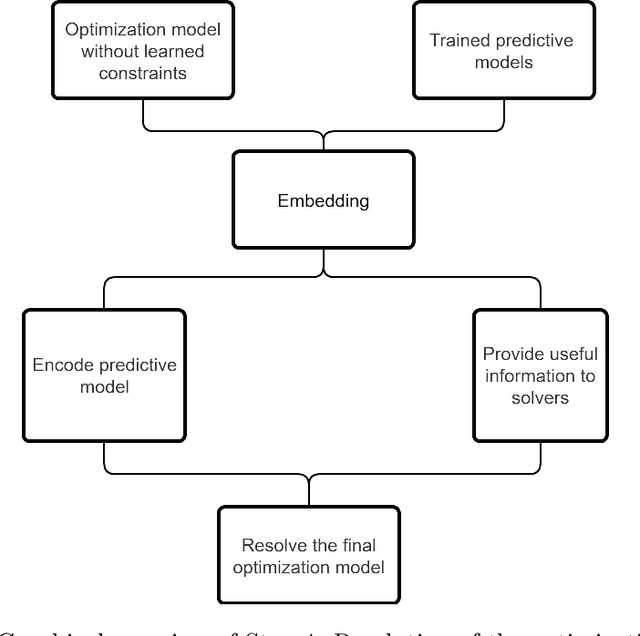
Many real-life optimization problems frequently contain one or more constraints or objectives for which there are no explicit formulas. If data is however available, these data can be used to learn the constraints. The benefits of this approach are clearly seen, however there is a need for this process to be carried out in a structured manner. This paper therefore provides a framework for Optimization with Constraint Learning (OCL) which we believe will help to formalize and direct the process of learning constraints from data. This framework includes the following steps: (i) setup of the conceptual optimization model, (ii) data gathering and preprocessing, (iii) selection and training of predictive models, (iv) resolution of the optimization model, and (v) verification and improvement of the optimization model. We then review the recent OCL literature in light of this framework, and highlight current trends, as well as areas for future research.