Mixed-Integer Optimization with Constraint Learning

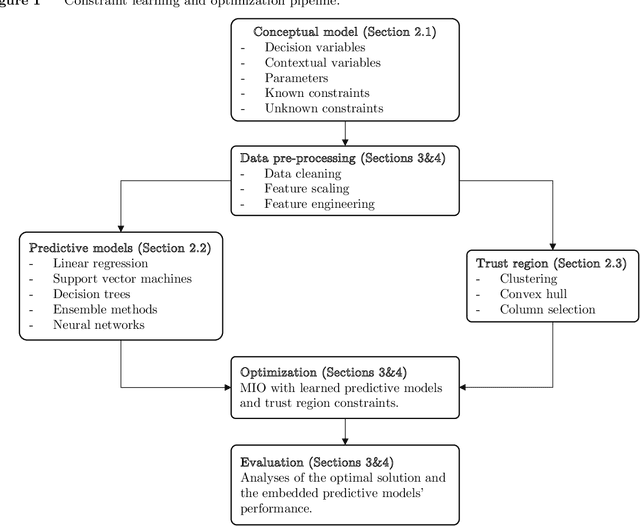
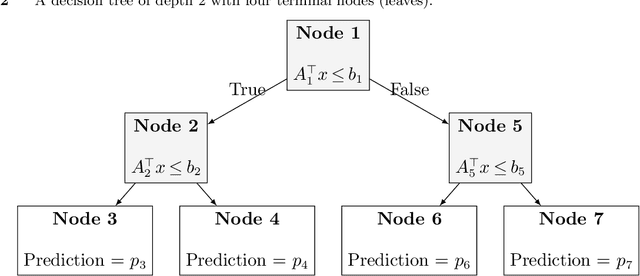
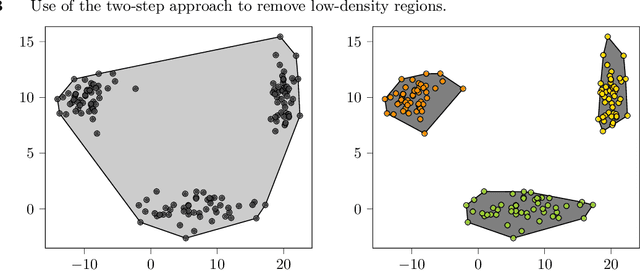
We establish a broad methodological foundation for mixed-integer optimization with learned constraints. We propose an end-to-end pipeline for data-driven decision making in which constraints and objectives are directly learned from data using machine learning, and the trained models are embedded in an optimization formulation. We exploit the mixed-integer optimization-representability of many machine learning methods, including linear models, decision trees, ensembles, and multi-layer perceptrons. The consideration of multiple methods allows us to capture various underlying relationships between decisions, contextual variables, and outcomes. We also characterize a decision trust region using the convex hull of the observations, to ensure credible recommendations and avoid extrapolation. We efficiently incorporate this representation using column generation and clustering. In combination with domain-driven constraints and objective terms, the embedded models and trust region define a mixed-integer optimization problem for prescription generation. We implement this framework as a Python package (OptiCL) for practitioners. We demonstrate the method in both chemotherapy optimization and World Food Programme planning. The case studies illustrate the benefit of the framework in generating high-quality prescriptions, the value added by the trust region, the incorporation of multiple machine learning methods, and the inclusion of multiple learned constraints.

Optimization with Constraint Learning: A Framework and Survey

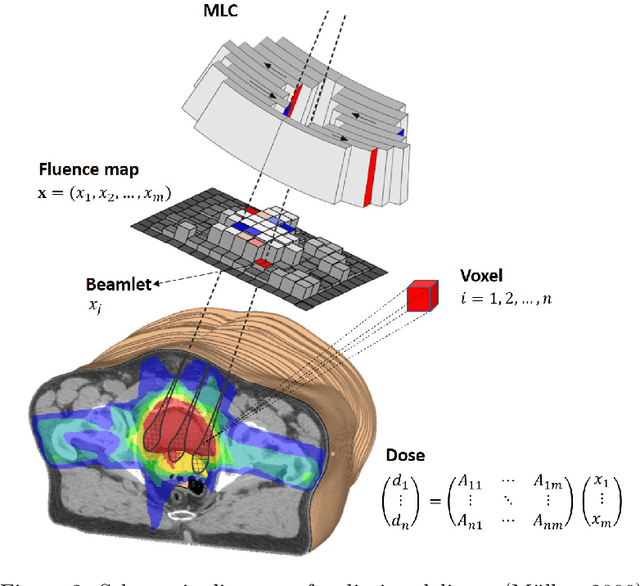
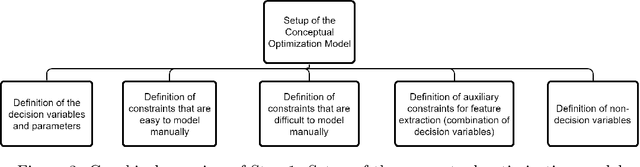
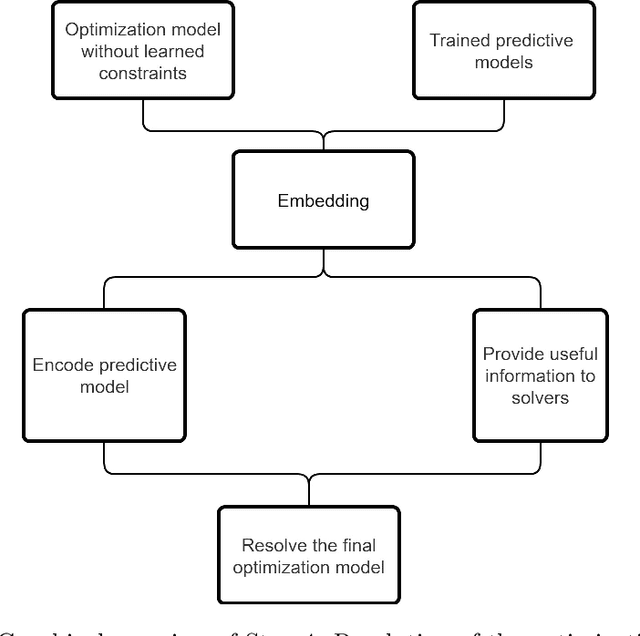
Many real-life optimization problems frequently contain one or more constraints or objectives for which there are no explicit formulas. If data is however available, these data can be used to learn the constraints. The benefits of this approach are clearly seen, however there is a need for this process to be carried out in a structured manner. This paper therefore provides a framework for Optimization with Constraint Learning (OCL) which we believe will help to formalize and direct the process of learning constraints from data. This framework includes the following steps: (i) setup of the conceptual optimization model, (ii) data gathering and preprocessing, (iii) selection and training of predictive models, (iv) resolution of the optimization model, and (v) verification and improvement of the optimization model. We then review the recent OCL literature in light of this framework, and highlight current trends, as well as areas for future research.