Graph-based Tabular Deep Learning Should Learn Feature Interactions, Not Just Make Predictions

Despite recent progress, deep learning methods for tabular data still struggle to compete with traditional tree-based models. A key challenge lies in modeling complex, dataset-specific feature interactions that are central to tabular data. Graph-based tabular deep learning (GTDL) methods aim to address this by representing features and their interactions as graphs. However, existing methods predominantly optimize predictive accuracy, neglecting accurate modeling of the graph structure. This position paper argues that GTDL should move beyond prediction-centric objectives and prioritize the explicit learning and evaluation of feature interactions. Using synthetic datasets with known ground-truth graph structures, we show that existing GTDL methods fail to recover meaningful feature interactions. Moreover, enforcing the true interaction structure improves predictive performance. This highlights the need for GTDL methods to prioritize quantitative evaluation and accurate structural learning. We call for a shift toward structure-aware modeling as a foundation for building GTDL systems that are not only accurate but also interpretable, trustworthy, and grounded in domain understanding.

Coherent Local Explanations for Mathematical Optimization

The surge of explainable artificial intelligence methods seeks to enhance transparency and explainability in machine learning models. At the same time, there is a growing demand for explaining decisions taken through complex algorithms used in mathematical optimization. However, current explanation methods do not take into account the structure of the underlying optimization problem, leading to unreliable outcomes. In response to this need, we introduce Coherent Local Explanations for Mathematical Optimization (CLEMO). CLEMO provides explanations for multiple components of optimization models, the objective value and decision variables, which are coherent with the underlying model structure. Our sampling-based procedure can provide explanations for the behavior of exact and heuristic solution algorithms. The effectiveness of CLEMO is illustrated by experiments for the shortest path problem, the knapsack problem, and the vehicle routing problem.

High-Dimensional Bayesian Structure Learning in Gaussian Graphical Models using Marginal Pseudo-Likelihood

Gaussian graphical models depict the conditional dependencies between variables within a multivariate normal distribution in a graphical format. The identification of these graph structures is an area known as structure learning. However, when utilizing Bayesian methodologies in structure learning, computational complexities can arise, especially with high-dimensional graphs surpassing 250 nodes. This paper introduces two innovative search algorithms that employ marginal pseudo-likelihood to address this computational challenge. These methods can swiftly generate reliable estimations for problems encompassing 1000 variables in just a few minutes on standard computers. For those interested in practical applications, the code supporting this new approach is made available through the R package BDgraph.

Learning with Subset Stacking

We propose a new algorithm that learns from a set of input-output pairs. Our algorithm is designed for populations where the relation between the input variables and the output variable exhibits a heterogeneous behavior across the predictor space. The algorithm starts with generating subsets that are concentrated around random points in the input space. This is followed by training a local predictor for each subset. Those predictors are then combined in a novel way to yield an overall predictor. We call this algorithm "LEarning with Subset Stacking" or LESS, due to its resemblance to method of stacking regressors. We compare the testing performance of LESS with the state-of-the-art methods on several datasets. Our comparison shows that LESS is a competitive supervised learning method. Moreover, we observe that LESS is also efficient in terms of computation time and it allows a straightforward parallel implementation.

Bolstering Stochastic Gradient Descent with Model Building

Stochastic gradient descent method and its variants constitute the core optimization algorithms that achieve good convergence rates for solving machine learning problems. These rates are obtained especially when these algorithms are fine-tuned for the application at hand. Although this tuning process can require large computational costs, recent work has shown that these costs can be reduced by line search methods that iteratively adjust the stepsize. We propose an alternative approach to stochastic line search by using a new algorithm based on forward step model building. This model building step incorporates a second-order information that allows adjusting not only the stepsize but also the search direction. Noting that deep learning model parameters come in groups (layers of tensors), our method builds its model and calculates a new step for each parameter group. This novel diagonalization approach makes the selected step lengths adaptive. We provide convergence rate analysis, and experimentally show that the proposed algorithm achieves faster convergence and better generalization in most problems. Moreover, our experiments show that the proposed method is quite robust as it converges for a wide range of initial stepsizes.

Mixed-Integer Optimization with Constraint Learning

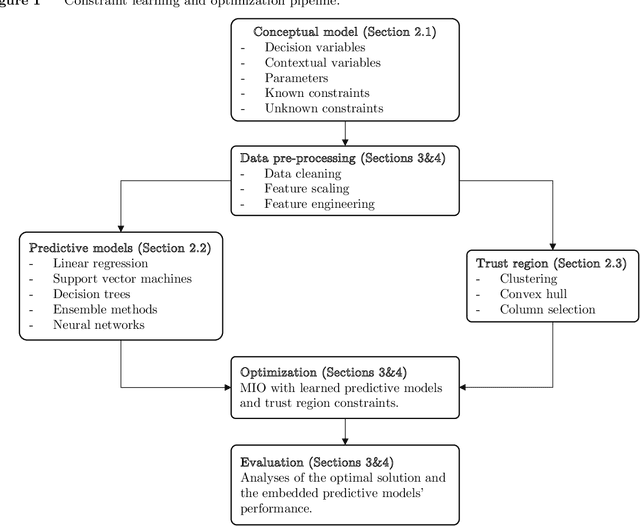
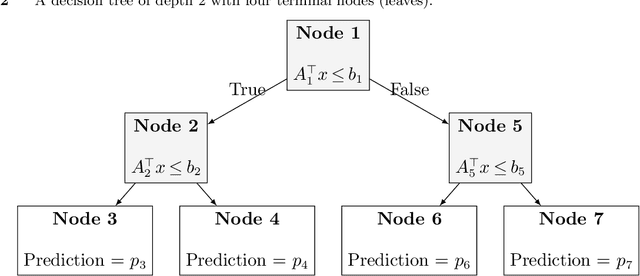
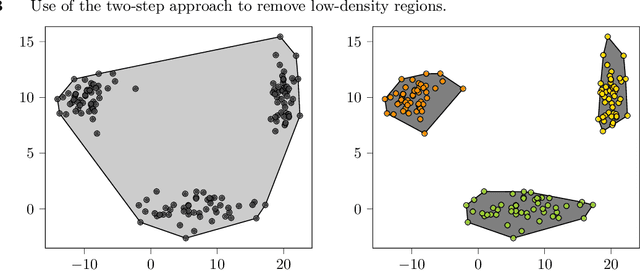
We establish a broad methodological foundation for mixed-integer optimization with learned constraints. We propose an end-to-end pipeline for data-driven decision making in which constraints and objectives are directly learned from data using machine learning, and the trained models are embedded in an optimization formulation. We exploit the mixed-integer optimization-representability of many machine learning methods, including linear models, decision trees, ensembles, and multi-layer perceptrons. The consideration of multiple methods allows us to capture various underlying relationships between decisions, contextual variables, and outcomes. We also characterize a decision trust region using the convex hull of the observations, to ensure credible recommendations and avoid extrapolation. We efficiently incorporate this representation using column generation and clustering. In combination with domain-driven constraints and objective terms, the embedded models and trust region define a mixed-integer optimization problem for prescription generation. We implement this framework as a Python package (OptiCL) for practitioners. We demonstrate the method in both chemotherapy optimization and World Food Programme planning. The case studies illustrate the benefit of the framework in generating high-quality prescriptions, the value added by the trust region, the incorporation of multiple machine learning methods, and the inclusion of multiple learned constraints.

Low-dimensional Interpretable Kernels with Conic Discriminant Functions for Classification

Kernels are often developed and used as implicit mapping functions that show impressive predictive power due to their high-dimensional feature space representations. In this study, we gradually construct a series of simple feature maps that lead to a collection of interpretable low-dimensional kernels. At each step, we keep the original features and make sure that the increase in the dimension of input data is extremely low, so that the resulting discriminant functions remain interpretable and amenable to fast training. Despite our persistence on interpretability, we obtain high accuracy results even without in-depth hyperparameter tuning. Comparison of our results against several well-known kernels on benchmark datasets show that the proposed kernels are competitive in terms of prediction accuracy, while the training times are significantly lower than those obtained with state-of-the-art kernel implementations.

Rule Covering for Interpretation and Boosting

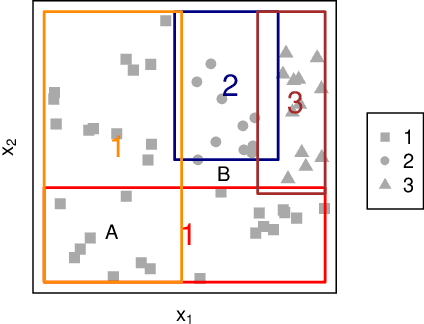
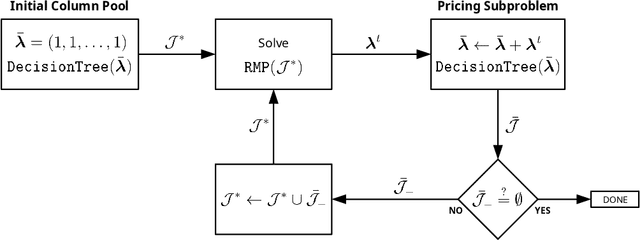
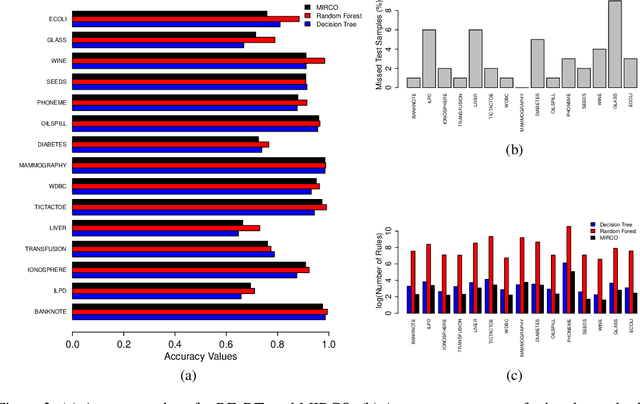
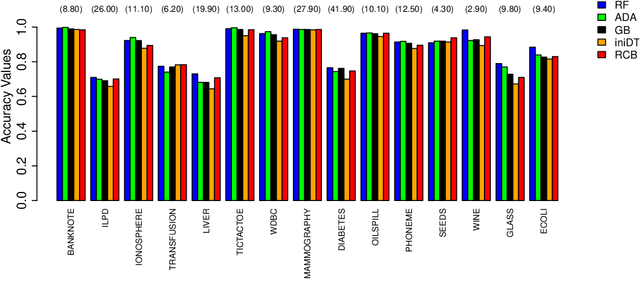
We propose two algorithms for interpretation and boosting of tree-based ensemble methods. Both algorithms make use of mathematical programming models that are constructed with a set of rules extracted from an ensemble of decision trees. The objective is to obtain the minimum total impurity with the least number of rules that cover all the samples. The first algorithm uses the collection of decision trees obtained from a trained random forest model. Our numerical results show that the proposed rule covering approach selects only a few rules that could be used for interpreting the random forest model. Moreover, the resulting set of rules closely matches the accuracy level of the random forest model. Inspired by the column generation algorithm in linear programming, our second algorithm uses a rule generation scheme for boosting decision trees. We use the dual optimal solutions of the linear programming models as sample weights to obtain only those rules that would improve the accuracy. With a computational study, we observe that our second algorithm performs competitively with the other well-known boosting methods. Our implementations also demonstrate that both algorithms can be trivially coupled with the existing random forest and decision tree packages.