Counterfactual Explanations for Linear Optimization

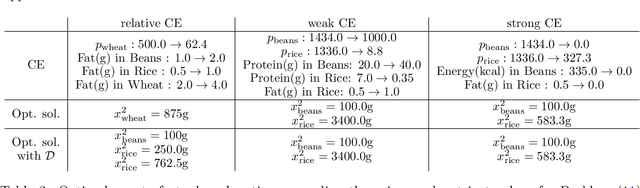
The concept of counterfactual explanations (CE) has emerged as one of the important concepts to understand the inner workings of complex AI systems. In this paper, we translate the idea of CEs to linear optimization and propose, motivate, and analyze three different types of CEs: strong, weak, and relative. While deriving strong and weak CEs appears to be computationally intractable, we show that calculating relative CEs can be done efficiently. By detecting and exploiting the hidden convex structure of the optimization problem that arises in the latter case, we show that obtaining relative CEs can be done in the same magnitude of time as solving the original linear optimization problem. This is confirmed by an extensive numerical experiment study on the NETLIB library.

From Large Language Models and Optimization to Decision Optimization CoPilot: A Research Manifesto

Significantly simplifying the creation of optimization models for real-world business problems has long been a major goal in applying mathematical optimization more widely to important business and societal decisions. The recent capabilities of Large Language Models (LLMs) present a timely opportunity to achieve this goal. Therefore, we propose research at the intersection of LLMs and optimization to create a Decision Optimization CoPilot (DOCP) - an AI tool designed to assist any decision maker, interacting in natural language to grasp the business problem, subsequently formulating and solving the corresponding optimization model. This paper outlines our DOCP vision and identifies several fundamental requirements for its implementation. We describe the state of the art through a literature survey and experiments using ChatGPT. We show that a) LLMs already provide substantial novel capabilities relevant to a DOCP, and b) major research challenges remain to be addressed. We also propose possible research directions to overcome these gaps. We also see this work as a call to action to bring together the LLM and optimization communities to pursue our vision, thereby enabling much more widespread improved decision-making.

Neur2BiLO: Neural Bilevel Optimization

Bilevel optimization deals with nested problems in which a leader takes the first decision to minimize their objective function while accounting for a follower's best-response reaction. Constrained bilevel problems with integer variables are particularly notorious for their hardness. While exact solvers have been proposed for mixed-integer linear bilevel optimization, they tend to scale poorly with problem size and are hard to generalize to the non-linear case. On the other hand, problem-specific algorithms (exact and heuristic) are limited in scope. Under a data-driven setting in which similar instances of a bilevel problem are solved routinely, our proposed framework, Neur2BiLO, embeds a neural network approximation of the leader's or follower's value function, trained via supervised regression, into an easy-to-solve mixed-integer program. Neur2BiLO serves as a heuristic that produces high-quality solutions extremely fast for the bilevel knapsack interdiction problem, the "critical node game" from network security, a donor-recipient healthcare problem, and discrete network design from transportation planning. These problems are diverse in that they have linear or non-linear objectives/constraints and integer or mixed-integer variables, making Neur2BiLO unique in its versatility.

Neur2RO: Neural Two-Stage Robust Optimization

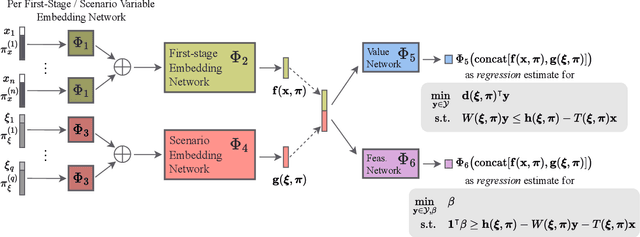
Robust optimization provides a mathematical framework for modeling and solving decision-making problems under worst-case uncertainty. This work addresses two-stage robust optimization (2RO) problems (also called adjustable robust optimization), wherein first-stage and second-stage decisions are made before and after uncertainty is realized, respectively. This results in a nested min-max-min optimization problem which is extremely challenging computationally, especially when the decisions are discrete. We propose Neur2RO, an efficient machine learning-driven instantiation of column-and-constraint generation (CCG), a classical iterative algorithm for 2RO. Specifically, we learn to estimate the value function of the second-stage problem via a novel neural network architecture that is easy to optimize over by design. Embedding our neural network into CCG yields high-quality solutions quickly as evidenced by experiments on two 2RO benchmarks, knapsack and capital budgeting. For knapsack, Neur2RO finds solutions that are within roughly $2\%$ of the best-known values in a few seconds compared to the three hours of the state-of-the-art exact branch-and-price algorithm; for larger and more complex instances, Neur2RO finds even better solutions. For capital budgeting, Neur2RO outperforms three variants of the $k$-adaptability algorithm, particularly on the largest instances, with a 5 to 10-fold reduction in solution time. Our code and data are available at https://github.com/khalil-research/Neur2RO.

Finding Regions of Counterfactual Explanations via Robust Optimization

Counterfactual explanations play an important role in detecting bias and improving the explainability of data-driven classification models. A counterfactual explanation (CE) is a minimal perturbed data point for which the decision of the model changes. Most of the existing methods can only provide one CE, which may not be achievable for the user. In this work we derive an iterative method to calculate robust CEs, i.e. CEs that remain valid even after the features are slightly perturbed. To this end, our method provides a whole region of CEs allowing the user to choose a suitable recourse to obtain a desired outcome. We use algorithmic ideas from robust optimization and prove convergence results for the most common machine learning methods including logistic regression, decision trees, random forests, and neural networks. Our experiments show that our method can efficiently generate globally optimal robust CEs for a variety of common data sets and classification models.

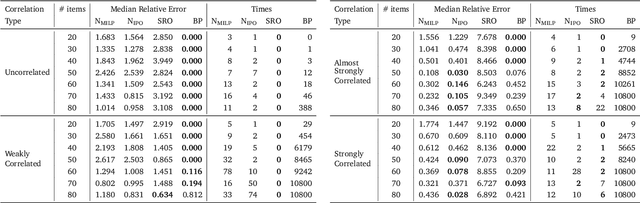
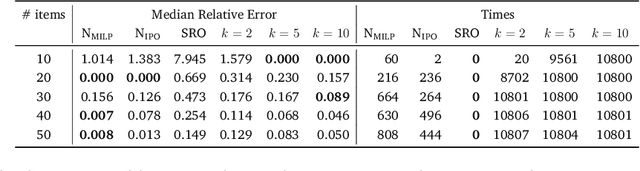
Data-driven Prediction of Relevant Scenarios for Robust Optimization

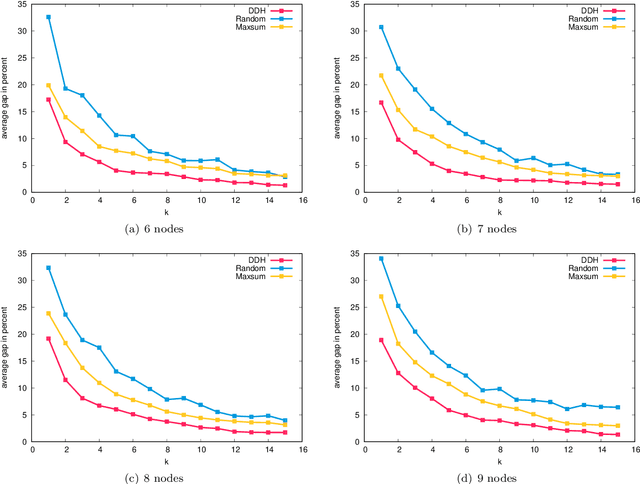
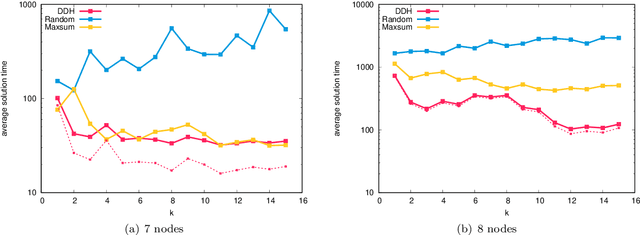
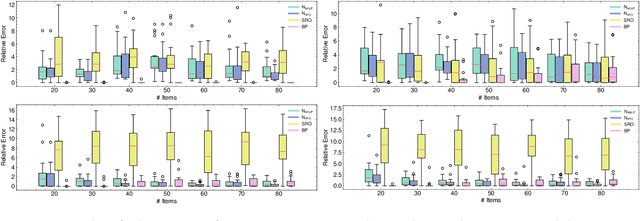
In this work we study robust one- and two-stage problems with discrete uncertainty sets which are known to be hard to solve even if the underlying deterministic problem is easy. Popular solution methods iteratively generate scenario constraints and possibly second-stage variables. This way, by solving a sequence of smaller problems, it is often possible to avoid the complexity of considering all scenarios simultaneously. A key ingredient for the performance of the iterative methods is a good selection of start scenarios. In this paper we propose a data-driven heuristic to seed the iterative solution method with a set of starting scenarios that provide a strong lower bound early in the process, and result in considerably smaller overall solution times compared to other benchmark methods. Our heuristic learns the relevance of a scenario by extracting information from training data based on a combined similarity measure between robust problem instances and single scenarios. Our experiments show that predicting even a small number of good start scenarios by our method can considerably reduce the computation time of the iterative methods.

Ensemble Methods for Robust Support Vector Machines using Integer Programming

In this work we study binary classification problems where we assume that our training data is subject to uncertainty, i.e. the precise data points are not known. To tackle this issue in the field of robust machine learning the aim is to develop models which are robust against small perturbations in the training data. We study robust support vector machines (SVM) and extend the classical approach by an ensemble method which iteratively solves a non-robust SVM on different perturbations of the dataset, where the perturbations are derived by an adversarial problem. Afterwards for classification of an unknown data point we perform a majority vote of all calculated SVM solutions. We study three different variants for the adversarial problem, the exact problem, a relaxed variant and an efficient heuristic variant. While the exact and the relaxed variant can be modeled using integer programming formulations, the heuristic one can be implemented by an easy and efficient algorithm. All derived methods are tested on random and realistic datasets and the results indicate that the derived ensemble methods have a much more stable behaviour when changing the protection level compared to the classical robust SVM model.

Efficient and Robust Mixed-Integer Optimization Methods for Training Binarized Deep Neural Networks

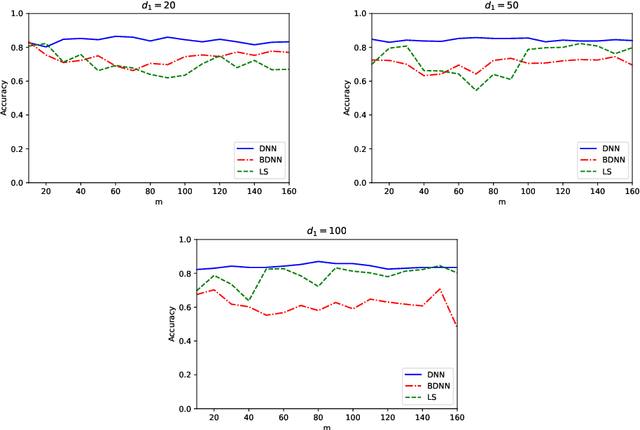
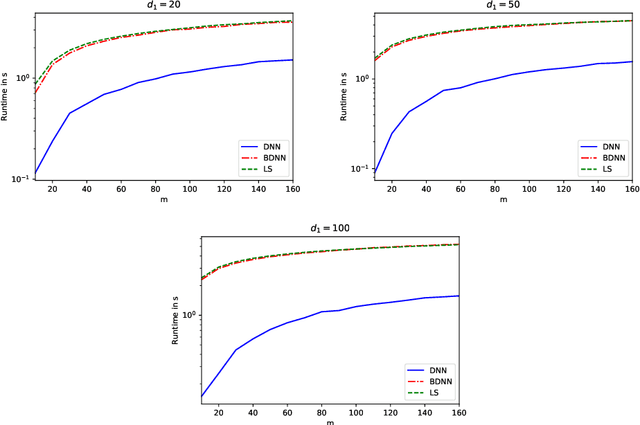
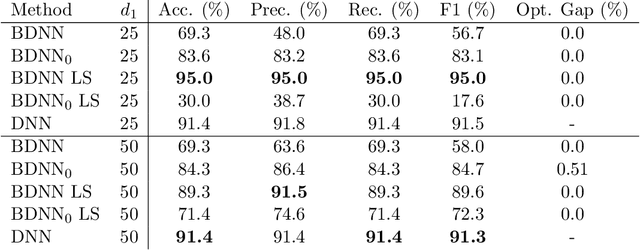
Compared to classical deep neural networks its binarized versions can be useful for applications on resource-limited devices due to their reduction in memory consumption and computational demands. In this work we study deep neural networks with binary activation functions and continuous or integer weights (BDNN). We show that the BDNN can be reformulated as a mixed-integer linear program with bounded weight space which can be solved to global optimality by classical mixed-integer programming solvers. Additionally, a local search heuristic is presented to calculate locally optimal networks. Furthermore to improve efficiency we present an iterative data-splitting heuristic which iteratively splits the training set into smaller subsets by using the k-mean method. Afterwards all data points in a given subset are forced to follow the same activation pattern, which leads to a much smaller number of integer variables in the mixed-integer programming formulation and therefore to computational improvements. Finally for the first time a robust model is presented which enforces robustness of the BDNN during training. All methods are tested on random and real datasets and our results indicate that all models can often compete with or even outperform classical DNNs on small network architectures confirming the viability for applications having restricted memory or computing power.

Data-Driven Robust Optimization using Unsupervised Deep Learning

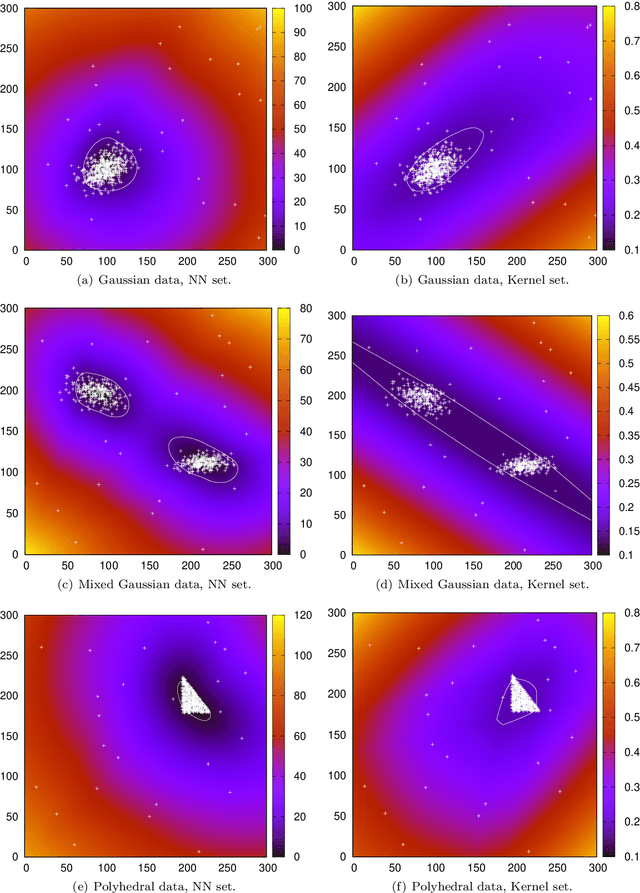
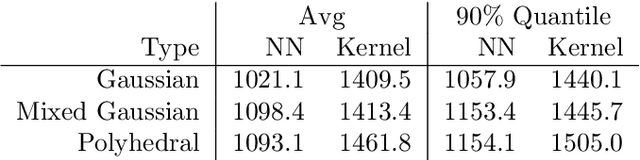
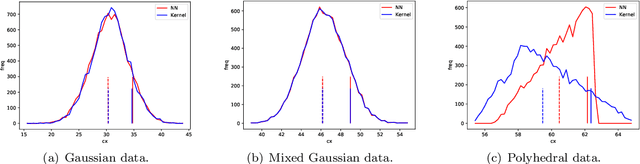
Robust optimization has been established as a leading methodology to approach decision problems under uncertainty. To derive a robust optimization model, a central ingredient is to identify a suitable model for uncertainty, which is called the uncertainty set, containing all scenarios against which we wish to protect. An ongoing challenge in the recent literature is to derive uncertainty sets from given historical data. In this paper we use an unsupervised deep learning method to construct non-convex uncertainty sets from data, which have a more complex structure than the typically considered sets. We show that the trained neural networks can be integrated into a robust optimization model by formulating the adversarial problem as a convex quadratic mixed-integer program. This allows us to derive robust solutions through an iterative scenario generation process. In extensive computational experiments, we compare this approach to a current state-of-the-art approach, which derives uncertainty sets by kernel-based support vector clustering. We find that uncertainty sets derived by the unsupervised deep learning method can give a better description of data, leading to robust solutions that considerably outperform the comparison method both with respect to objective value and feasibility.

An Integer Programming Approach to Deep Neural Networks with Binary Activation Functions

We study deep neural networks with binary activation functions (BDNN), i.e. the activation function only has two states. We show that the BDNN can be reformulated as a mixed-integer linear program which can be solved to global optimality by classical integer programming solvers. Additionally, a heuristic solution algorithm is presented and we study the model under data uncertainty, applying a two-stage robust optimization approach. We implemented our methods on random and real datasets and show that the heuristic version of the BDNN outperforms classical deep neural networks on the Breast Cancer Wisconsin dataset while performing worse on random data.