Farzaneh Mirzazadeh
From Large Language Models and Optimization to Decision Optimization CoPilot: A Research Manifesto
Feb 26, 2024



Abstract:Significantly simplifying the creation of optimization models for real-world business problems has long been a major goal in applying mathematical optimization more widely to important business and societal decisions. The recent capabilities of Large Language Models (LLMs) present a timely opportunity to achieve this goal. Therefore, we propose research at the intersection of LLMs and optimization to create a Decision Optimization CoPilot (DOCP) - an AI tool designed to assist any decision maker, interacting in natural language to grasp the business problem, subsequently formulating and solving the corresponding optimization model. This paper outlines our DOCP vision and identifies several fundamental requirements for its implementation. We describe the state of the art through a literature survey and experiments using ChatGPT. We show that a) LLMs already provide substantial novel capabilities relevant to a DOCP, and b) major research challenges remain to be addressed. We also propose possible research directions to overcome these gaps. We also see this work as a call to action to bring together the LLM and optimization communities to pursue our vision, thereby enabling much more widespread improved decision-making.
GC-Flow: A Graph-Based Flow Network for Effective Clustering
May 26, 2023



Abstract:Graph convolutional networks (GCNs) are \emph{discriminative models} that directly model the class posterior $p(y|\mathbf{x})$ for semi-supervised classification of graph data. While being effective, as a representation learning approach, the node representations extracted from a GCN often miss useful information for effective clustering, because the objectives are different. In this work, we design normalizing flows that replace GCN layers, leading to a \emph{generative model} that models both the class conditional likelihood $p(\mathbf{x}|y)$ and the class prior $p(y)$. The resulting neural network, GC-Flow, retains the graph convolution operations while being equipped with a Gaussian mixture representation space. It enjoys two benefits: it not only maintains the predictive power of GCN, but also produces well-separated clusters, due to the structuring of the representation space. We demonstrate these benefits on a variety of benchmark data sets. Moreover, we show that additional parameterization, such as that on the adjacency matrix used for graph convolutions, yields additional improvement in clustering.
Alleviating Label Switching with Optimal Transport
Nov 10, 2019

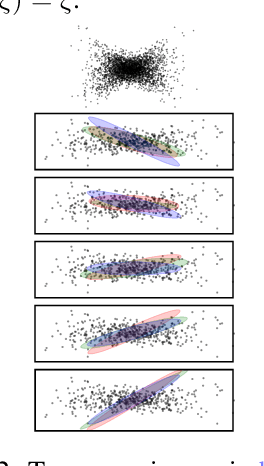
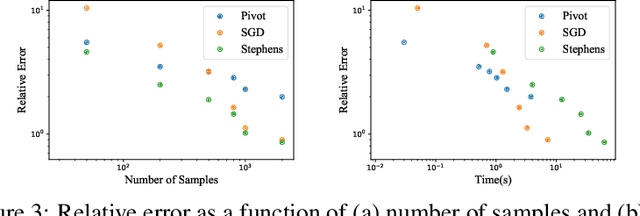
Abstract:Label switching is a phenomenon arising in mixture model posterior inference that prevents one from meaningfully assessing posterior statistics using standard Monte Carlo procedures. This issue arises due to invariance of the posterior under actions of a group; for example, permuting the ordering of mixture components has no effect on the likelihood. We propose a resolution to label switching that leverages machinery from optimal transport. Our algorithm efficiently computes posterior statistics in the quotient space of the symmetry group. We give conditions under which there is a meaningful solution to label switching and demonstrate advantages over alternative approaches on simulated and real data.
Hierarchical Optimal Transport for Document Representation
Jun 26, 2019
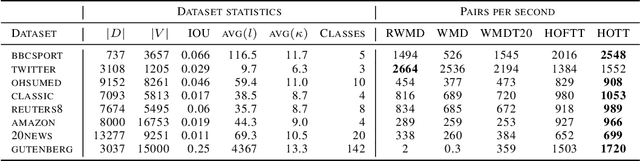
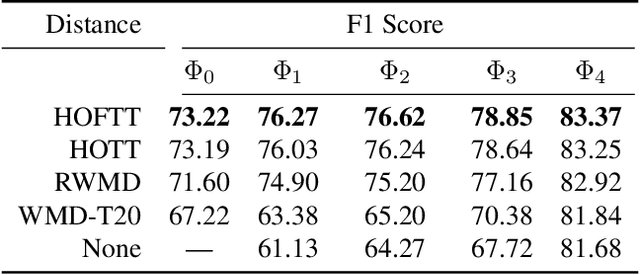

Abstract:The ability to measure similarity between documents enables intelligent summarization and analysis of large corpora. Past distances between documents suffer from either an inability to incorporate semantic similarities between words or from scalability issues. As an alternative, we introduce hierarchical optimal transport as a meta-distance between documents, where documents are modeled as distributions over topics, which themselves are modeled as distributions over words. We then solve an optimal transport problem on the smaller topic space to compute a similarity score. We give conditions on the topics under which this construction defines a distance, and we relate it to the word mover's distance. We evaluate our technique for $k$-NN classification and show better interpretability and scalability with comparable performance to current methods at a fraction of the cost.
BreGMN: scaled-Bregman Generative Modeling Networks
Jun 01, 2019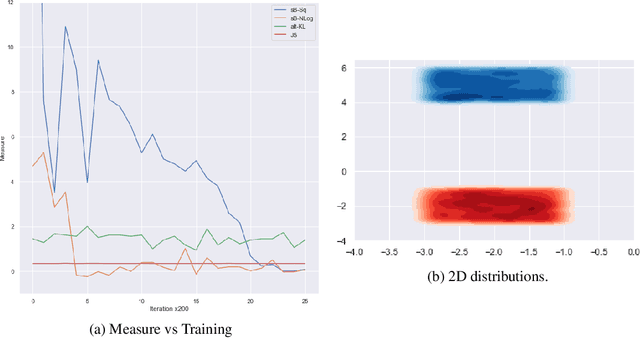
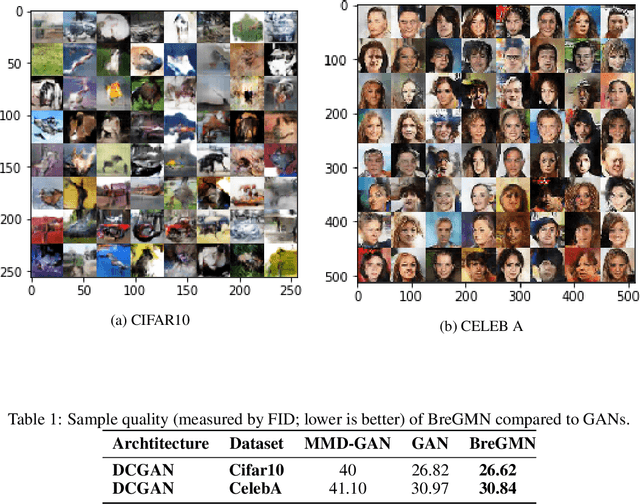

Abstract:The family of f-divergences is ubiquitously applied to generative modeling in order to adapt the distribution of the model to that of the data. Well-definedness of f-divergences, however, requires the distributions of the data and model to overlap completely in every time step of training. As a result, as soon as the support of distributions of data and model contain non-overlapping portions, gradient based training of the corresponding model becomes hopeless. Recent advances in generative modeling are full of remedies for handling this support mismatch problem: key ideas include either modifying the objective function to integral probability measures (IPMs) that are well-behaved even on disjoint probabilities, or optimizing a well-behaved variational lower bound instead of the true objective. We, on the other hand, establish that a complete change of the objective function is unnecessary, and instead an augmentation of the base measure of the problematic divergence can resolve the issue. Based on this observation, we propose a generative model which leverages the class of Scaled Bregman Divergences and generalizes both f-divergences and Bregman divergences. We analyze this class of divergences and show that with the appropriate choice of base measure it can resolve the support mismatch problem and incorporate geometric information. Finally, we study the performance of the proposed method and demonstrate promising results on MNIST, CelebA and CIFAR-10 datasets.
Learning Embeddings into Entropic Wasserstein Spaces
May 08, 2019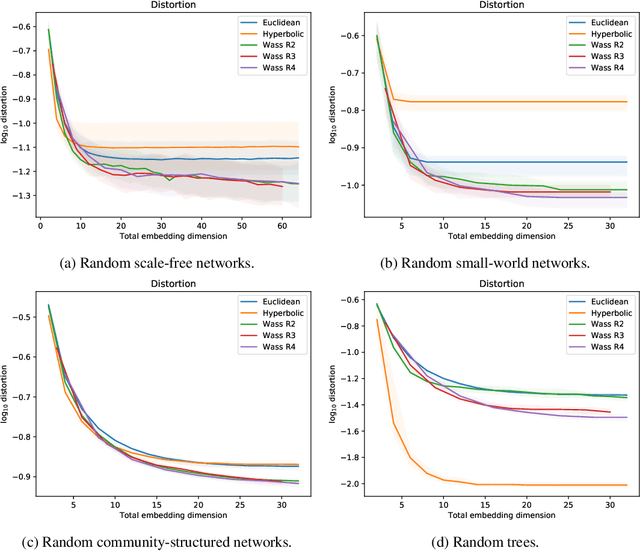

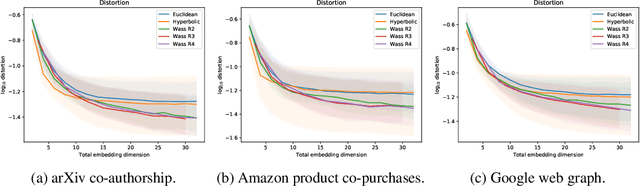

Abstract:Euclidean embeddings of data are fundamentally limited in their ability to capture latent semantic structures, which need not conform to Euclidean spatial assumptions. Here we consider an alternative, which embeds data as discrete probability distributions in a Wasserstein space, endowed with an optimal transport metric. Wasserstein spaces are much larger and more flexible than Euclidean spaces, in that they can successfully embed a wider variety of metric structures. We exploit this flexibility by learning an embedding that captures semantic information in the Wasserstein distance between embedded distributions. We examine empirically the representational capacity of our learned Wasserstein embeddings, showing that they can embed a wide variety of metric structures with smaller distortion than an equivalent Euclidean embedding. We also investigate an application to word embedding, demonstrating a unique advantage of Wasserstein embeddings: We can visualize the high-dimensional embedding directly, since it is a probability distribution on a low-dimensional space. This obviates the need for dimensionality reduction techniques like t-SNE for visualization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge