Partially Observed Trajectory Inference using Optimal Transport and a Dynamics Prior

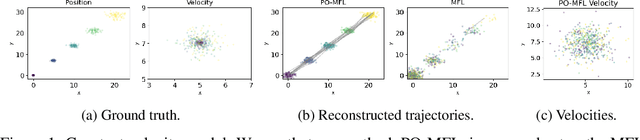
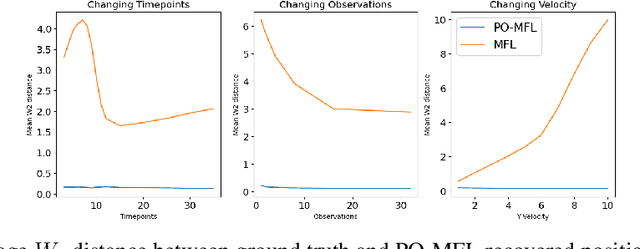
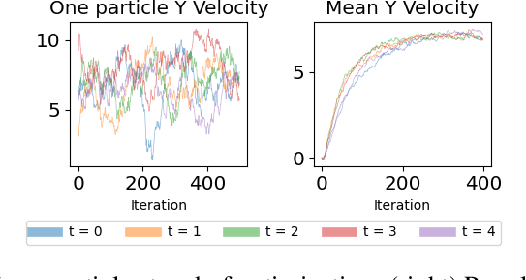
Trajectory inference seeks to recover the temporal dynamics of a population from snapshots of its (uncoupled) temporal marginals, i.e. where observed particles are not tracked over time. Lavenant et al. arXiv:2102.09204 addressed this challenging problem under a stochastic differential equation (SDE) model with a gradient-driven drift in the observed space, introducing a minimum entropy estimator relative to the Wiener measure. Chizat et al. arXiv:2205.07146 then provided a practical grid-free mean-field Langevin (MFL) algorithm using Schr\"odinger bridges. Motivated by the overwhelming success of observable state space models in the traditional paired trajectory inference problem (e.g. target tracking), we extend the above framework to a class of latent SDEs in the form of observable state space models. In this setting, we use partial observations to infer trajectories in the latent space under a specified dynamics model (e.g. the constant velocity/acceleration models from target tracking). We introduce PO-MFL to solve this latent trajectory inference problem and provide theoretical guarantees by extending the results of arXiv:2102.09204 to the partially observed setting. We leverage the MFL framework of arXiv:2205.07146, yielding an algorithm based on entropic OT between dynamics-adjusted adjacent time marginals. Experiments validate the robustness of our method and the exponential convergence of the MFL dynamics, and demonstrate significant outperformance over the latent-free method of arXiv:2205.07146 in key scenarios.

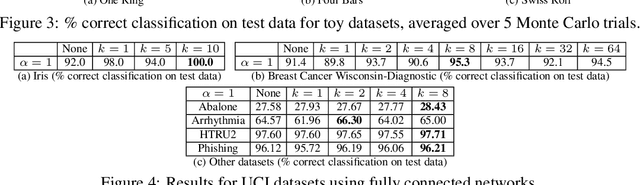
k-Mixup Regularization for Deep Learning via Optimal Transport

Mixup is a popular regularization technique for training deep neural networks that can improve generalization and increase adversarial robustness. It perturbs input training data in the direction of other randomly-chosen instances in the training set. To better leverage the structure of the data, we extend mixup to \emph{$k$-mixup} by perturbing $k$-batches of training points in the direction of other $k$-batches using displacement interpolation, interpolation under the Wasserstein metric. We demonstrate theoretically and in simulations that $k$-mixup preserves cluster and manifold structures, and we extend theory studying efficacy of standard mixup. Our empirical results show that training with $k$-mixup further improves generalization and robustness on benchmark datasets.

Incorporating Unlabeled Data into Distributionally Robust Learning

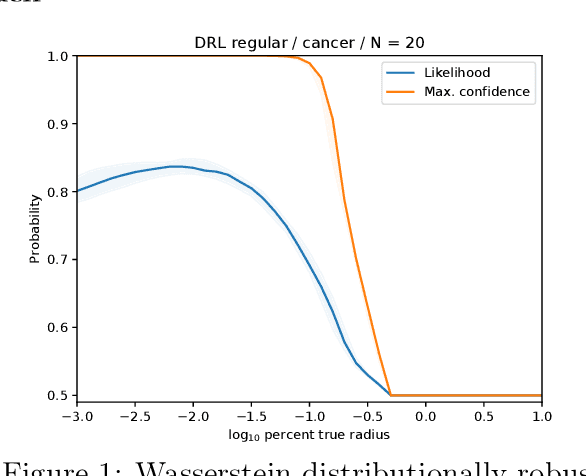
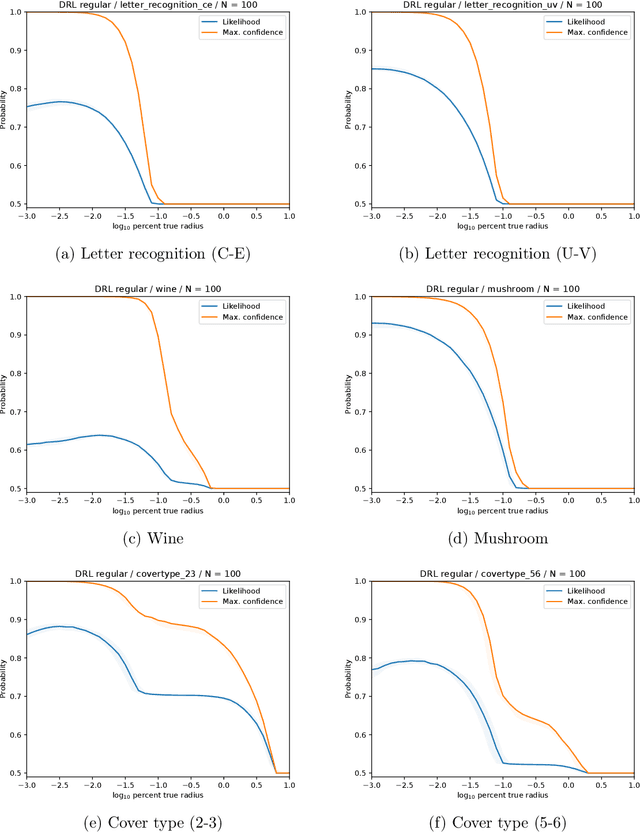
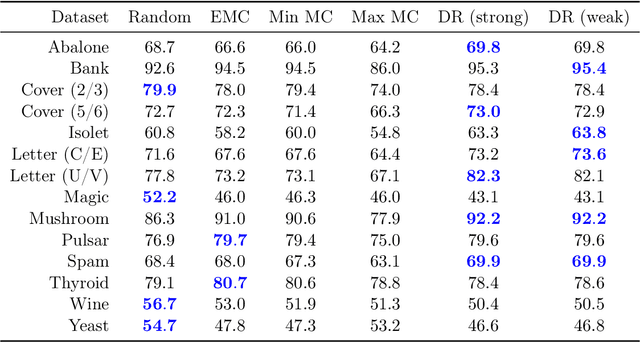
We study a robust alternative to empirical risk minimization called distributionally robust learning (DRL), in which one learns to perform against an adversary who can choose the data distribution from a specified set of distributions. We illustrate a problem with current DRL formulations, which rely on an overly broad definition of allowed distributions for the adversary, leading to learned classifiers that are unable to predict with any confidence. We propose a solution that incorporates unlabeled data into the DRL problem to further constrain the adversary. We show that this new formulation is tractable for stochastic gradient-based optimization and yields a computable guarantee on the future performance of the learned classifier, analogous to -- but tighter than -- guarantees from conventional DRL. We examine the performance of this new formulation on 14 real datasets and find that it often yields effective classifiers with nontrivial performance guarantees in situations where conventional DRL produces neither. Inspired by these results, we extend our DRL formulation to active learning with a novel, distributionally-robust version of the standard model-change heuristic. Our active learning algorithm often achieves superior learning performance to the original heuristic on real datasets.

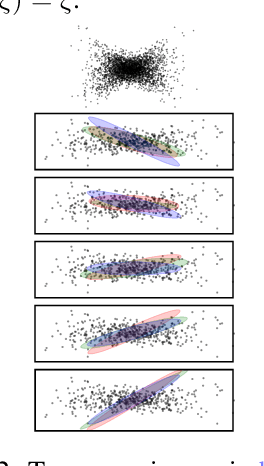
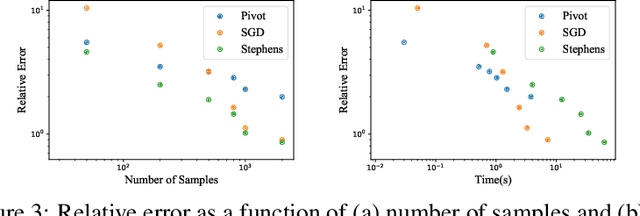
Alleviating Label Switching with Optimal Transport

Label switching is a phenomenon arising in mixture model posterior inference that prevents one from meaningfully assessing posterior statistics using standard Monte Carlo procedures. This issue arises due to invariance of the posterior under actions of a group; for example, permuting the ordering of mixture components has no effect on the likelihood. We propose a resolution to label switching that leverages machinery from optimal transport. Our algorithm efficiently computes posterior statistics in the quotient space of the symmetry group. We give conditions under which there is a meaningful solution to label switching and demonstrate advantages over alternative approaches on simulated and real data.

Hierarchical Optimal Transport for Document Representation

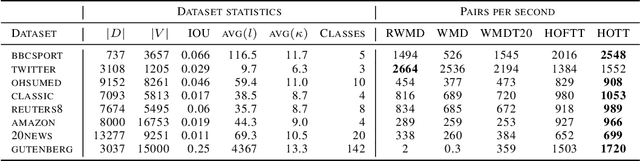
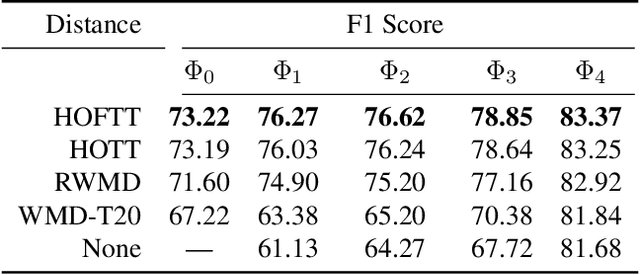
The ability to measure similarity between documents enables intelligent summarization and analysis of large corpora. Past distances between documents suffer from either an inability to incorporate semantic similarities between words or from scalability issues. As an alternative, we introduce hierarchical optimal transport as a meta-distance between documents, where documents are modeled as distributions over topics, which themselves are modeled as distributions over words. We then solve an optimal transport problem on the smaller topic space to compute a similarity score. We give conditions on the topics under which this construction defines a distance, and we relate it to the word mover's distance. We evaluate our technique for $k$-NN classification and show better interpretability and scalability with comparable performance to current methods at a fraction of the cost.

Stochastic Wasserstein Barycenters

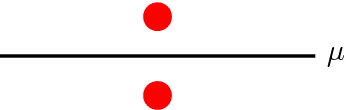
We present a stochastic algorithm to compute the barycenter of a set of probability distributions under the Wasserstein metric from optimal transport. Unlike previous approaches, our method extends to continuous input distributions and allows the support of the barycenter to be adjusted in each iteration. We tackle the problem without regularization, allowing us to recover a sharp output whose support is contained within the support of the true barycenter. We give examples where our algorithm recovers a more meaningful barycenter than previous work. Our method is versatile and can be extended to applications such as generating super samples from a given distribution and recovering blue noise approximations.