Incorporating Unlabeled Data into Distributionally Robust Learning
Paper and Code
Dec 18, 2019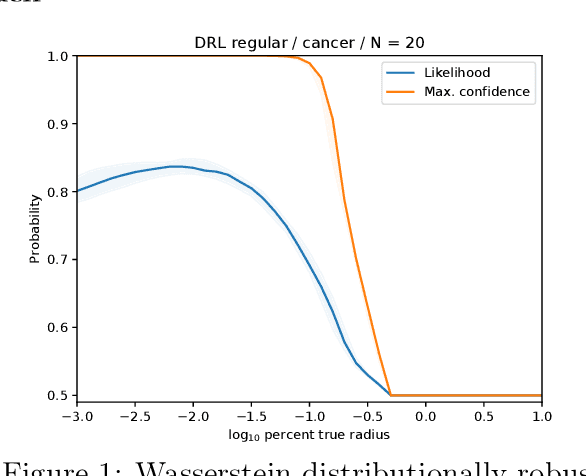

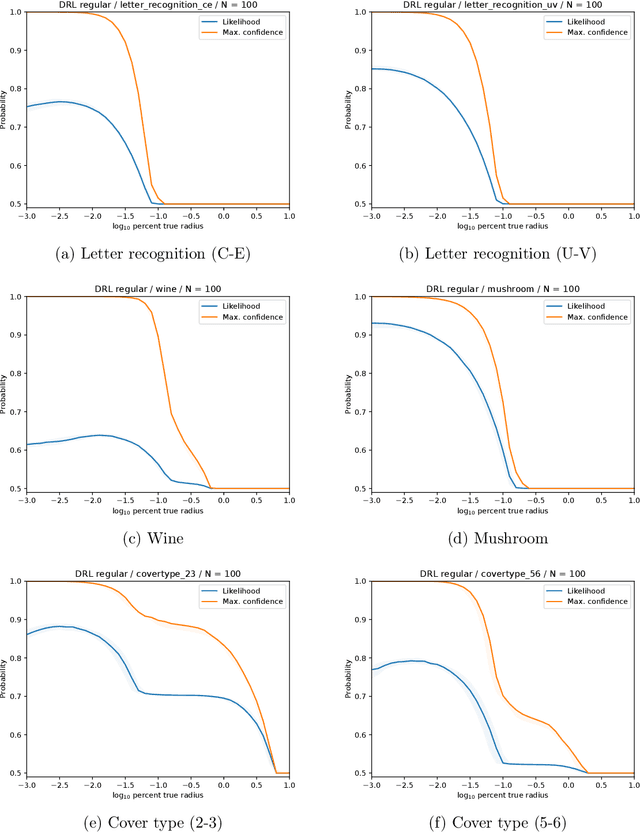
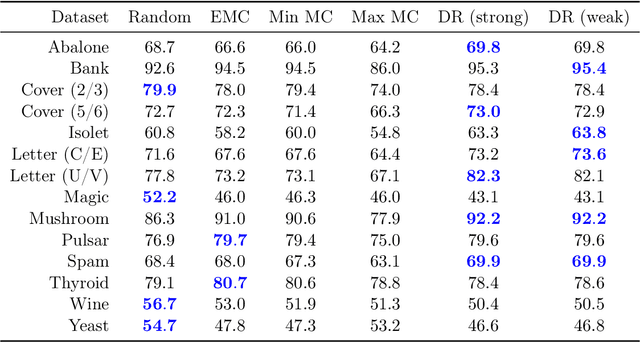
We study a robust alternative to empirical risk minimization called distributionally robust learning (DRL), in which one learns to perform against an adversary who can choose the data distribution from a specified set of distributions. We illustrate a problem with current DRL formulations, which rely on an overly broad definition of allowed distributions for the adversary, leading to learned classifiers that are unable to predict with any confidence. We propose a solution that incorporates unlabeled data into the DRL problem to further constrain the adversary. We show that this new formulation is tractable for stochastic gradient-based optimization and yields a computable guarantee on the future performance of the learned classifier, analogous to -- but tighter than -- guarantees from conventional DRL. We examine the performance of this new formulation on 14 real datasets and find that it often yields effective classifiers with nontrivial performance guarantees in situations where conventional DRL produces neither. Inspired by these results, we extend our DRL formulation to active learning with a novel, distributionally-robust version of the standard model-change heuristic. Our active learning algorithm often achieves superior learning performance to the original heuristic on real datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge