Partially Observed Trajectory Inference using Optimal Transport and a Dynamics Prior
Paper and Code
Jun 11, 2024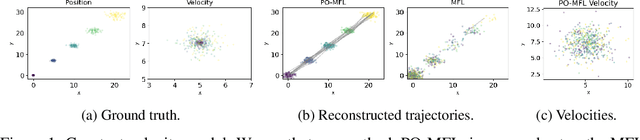
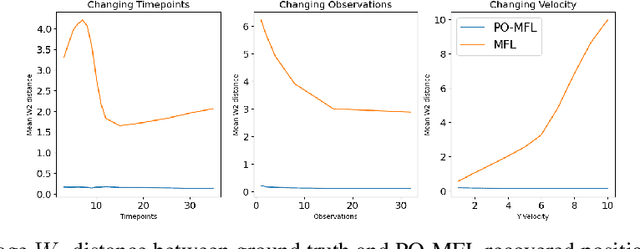


Trajectory inference seeks to recover the temporal dynamics of a population from snapshots of its (uncoupled) temporal marginals, i.e. where observed particles are not tracked over time. Lavenant et al. arXiv:2102.09204 addressed this challenging problem under a stochastic differential equation (SDE) model with a gradient-driven drift in the observed space, introducing a minimum entropy estimator relative to the Wiener measure. Chizat et al. arXiv:2205.07146 then provided a practical grid-free mean-field Langevin (MFL) algorithm using Schr\"odinger bridges. Motivated by the overwhelming success of observable state space models in the traditional paired trajectory inference problem (e.g. target tracking), we extend the above framework to a class of latent SDEs in the form of observable state space models. In this setting, we use partial observations to infer trajectories in the latent space under a specified dynamics model (e.g. the constant velocity/acceleration models from target tracking). We introduce PO-MFL to solve this latent trajectory inference problem and provide theoretical guarantees by extending the results of arXiv:2102.09204 to the partially observed setting. We leverage the MFL framework of arXiv:2205.07146, yielding an algorithm based on entropic OT between dynamics-adjusted adjacent time marginals. Experiments validate the robustness of our method and the exponential convergence of the MFL dynamics, and demonstrate significant outperformance over the latent-free method of arXiv:2205.07146 in key scenarios.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge