Hierarchical Optimal Transport for Document Representation

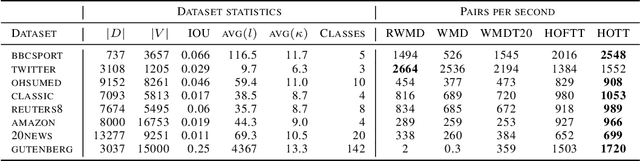
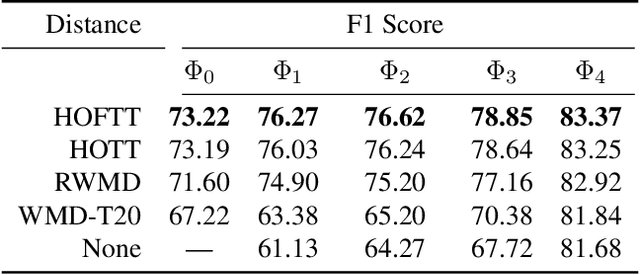
The ability to measure similarity between documents enables intelligent summarization and analysis of large corpora. Past distances between documents suffer from either an inability to incorporate semantic similarities between words or from scalability issues. As an alternative, we introduce hierarchical optimal transport as a meta-distance between documents, where documents are modeled as distributions over topics, which themselves are modeled as distributions over words. We then solve an optimal transport problem on the smaller topic space to compute a similarity score. We give conditions on the topics under which this construction defines a distance, and we relate it to the word mover's distance. We evaluate our technique for $k$-NN classification and show better interpretability and scalability with comparable performance to current methods at a fraction of the cost.