Learning Embeddings into Entropic Wasserstein Spaces
Paper and Code
May 08, 2019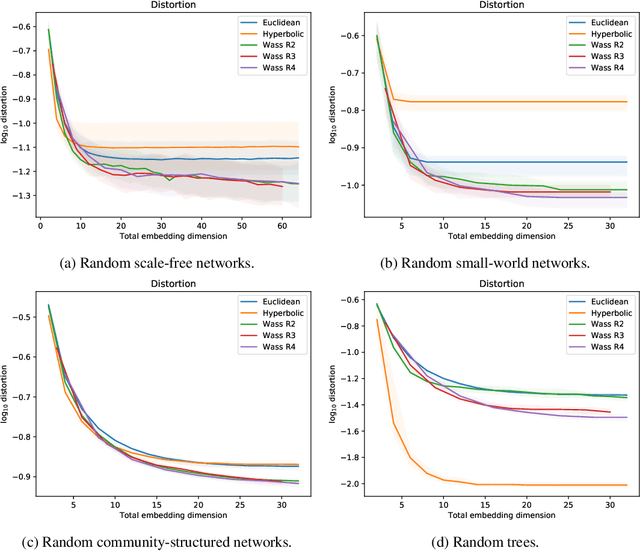

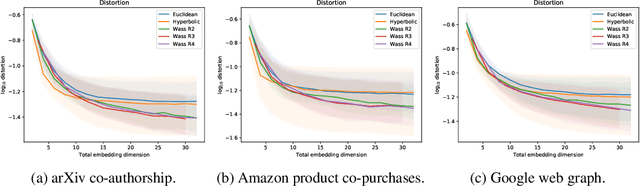

Euclidean embeddings of data are fundamentally limited in their ability to capture latent semantic structures, which need not conform to Euclidean spatial assumptions. Here we consider an alternative, which embeds data as discrete probability distributions in a Wasserstein space, endowed with an optimal transport metric. Wasserstein spaces are much larger and more flexible than Euclidean spaces, in that they can successfully embed a wider variety of metric structures. We exploit this flexibility by learning an embedding that captures semantic information in the Wasserstein distance between embedded distributions. We examine empirically the representational capacity of our learned Wasserstein embeddings, showing that they can embed a wide variety of metric structures with smaller distortion than an equivalent Euclidean embedding. We also investigate an application to word embedding, demonstrating a unique advantage of Wasserstein embeddings: We can visualize the high-dimensional embedding directly, since it is a probability distribution on a low-dimensional space. This obviates the need for dimensionality reduction techniques like t-SNE for visualization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge