This actually looks like that: Proto-BagNets for local and global interpretability-by-design

Interpretability is a key requirement for the use of machine learning models in high-stakes applications, including medical diagnosis. Explaining black-box models mostly relies on post-hoc methods that do not faithfully reflect the model's behavior. As a remedy, prototype-based networks have been proposed, but their interpretability is limited as they have been shown to provide coarse, unreliable, and imprecise explanations. In this work, we introduce Proto-BagNets, an interpretable-by-design prototype-based model that combines the advantages of bag-of-local feature models and prototype learning to provide meaningful, coherent, and relevant prototypical parts needed for accurate and interpretable image classification tasks. We evaluated the Proto-BagNet for drusen detection on publicly available retinal OCT data. The Proto-BagNet performed comparably to the state-of-the-art interpretable and non-interpretable models while providing faithful, accurate, and clinically meaningful local and global explanations. The code is available at https://github.com/kdjoumessi/Proto-BagNets.

Improved identification accuracy in equation learning via comprehensive $\boldsymbol{R^2}$-elimination and Bayesian model selection

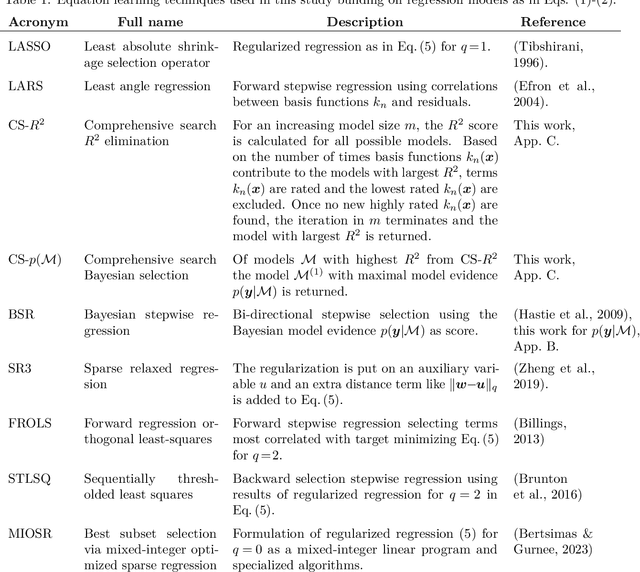
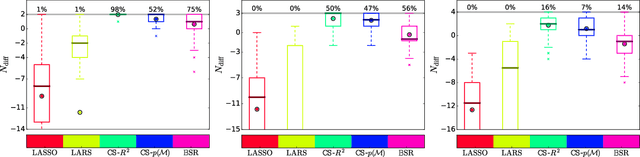
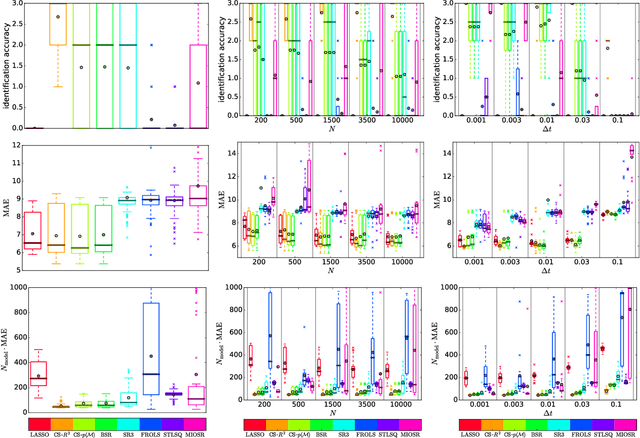
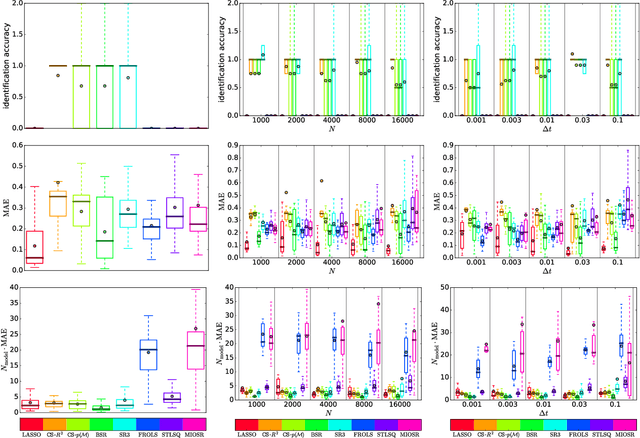
In the field of equation learning, exhaustively considering all possible equations derived from a basis function dictionary is infeasible. Sparse regression and greedy algorithms have emerged as popular approaches to tackle this challenge. However, the presence of multicollinearity poses difficulties for sparse regression techniques, and greedy steps may inadvertently exclude terms of the true equation, leading to reduced identification accuracy. In this article, we present an approach that strikes a balance between comprehensiveness and efficiency in equation learning. Inspired by stepwise regression, our approach combines the coefficient of determination, $R^2$, and the Bayesian model evidence, $p(\boldsymbol y|\mathcal M)$, in a novel way. Our procedure is characterized by a comprehensive search with just a minor reduction of the model space at each iteration step. With two flavors of our approach and the adoption of $p(\boldsymbol y|\mathcal M)$ for bi-directional stepwise regression, we present a total of three new avenues for equation learning. Through three extensive numerical experiments involving random polynomials and dynamical systems, we compare our approach against four state-of-the-art methods and two standard approaches. The results demonstrate that our comprehensive search approach surpasses all other methods in terms of identification accuracy. In particular, the second flavor of our approach establishes an efficient overfitting penalty solely based on $R^2$, which achieves highest rates of exact equation recovery.

A physics-informed neural network framework for modeling obstacle-related equations

Deep learning has been highly successful in some applications. Nevertheless, its use for solving partial differential equations (PDEs) has only been of recent interest with current state-of-the-art machine learning libraries, e.g., TensorFlow or PyTorch. Physics-informed neural networks (PINNs) are an attractive tool for solving partial differential equations based on sparse and noisy data. Here extend PINNs to solve obstacle-related PDEs which present a great computational challenge because they necessitate numerical methods that can yield an accurate approximation of the solution that lies above a given obstacle. The performance of the proposed PINNs is demonstrated in multiple scenarios for linear and nonlinear PDEs subject to regular and irregular obstacles.

Efficient and Robust Mixed-Integer Optimization Methods for Training Binarized Deep Neural Networks

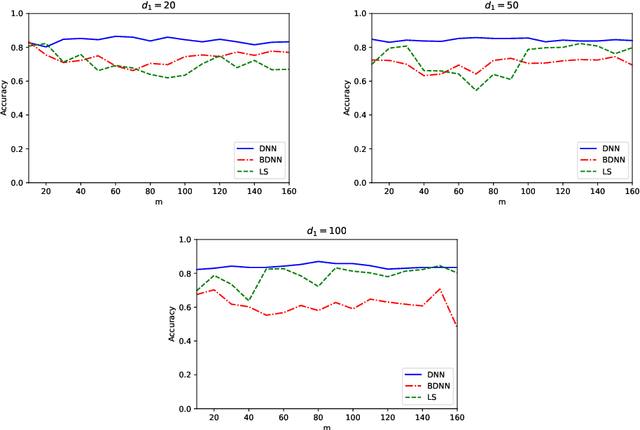
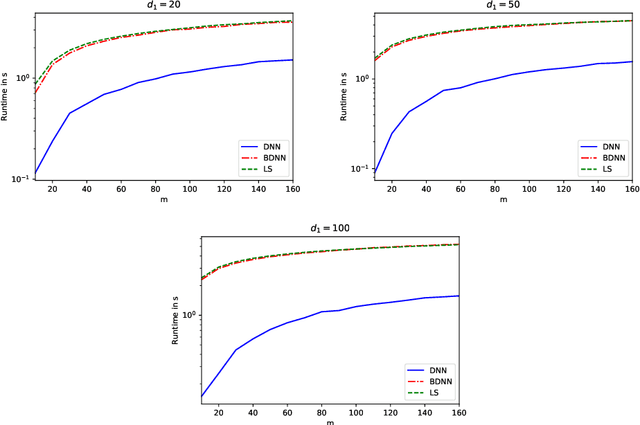
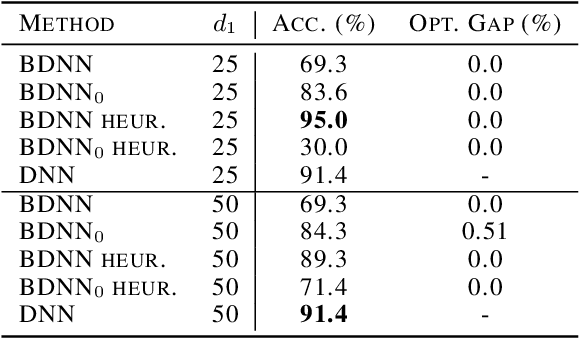
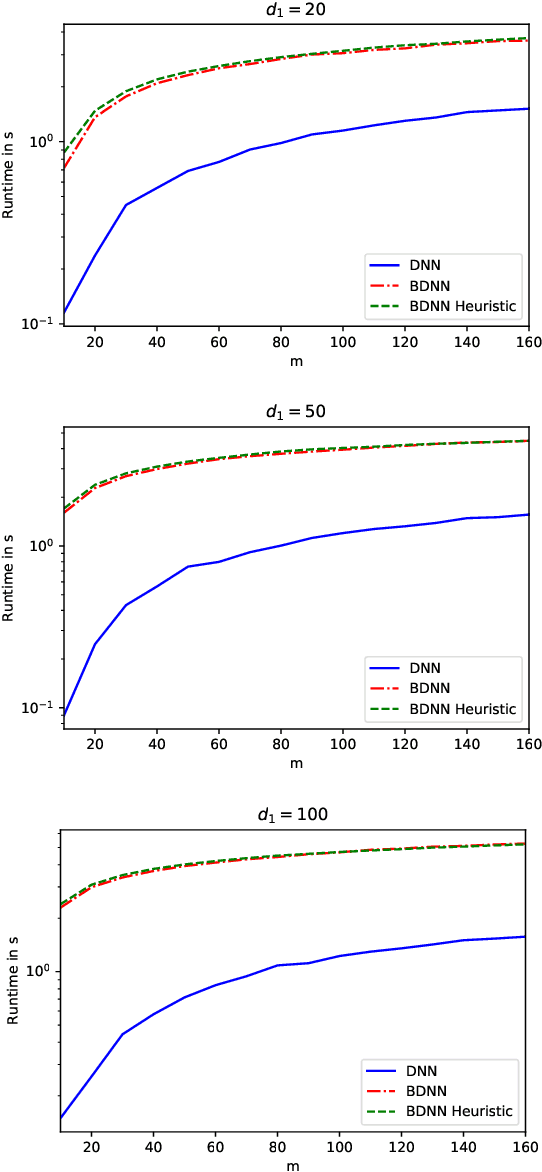
Compared to classical deep neural networks its binarized versions can be useful for applications on resource-limited devices due to their reduction in memory consumption and computational demands. In this work we study deep neural networks with binary activation functions and continuous or integer weights (BDNN). We show that the BDNN can be reformulated as a mixed-integer linear program with bounded weight space which can be solved to global optimality by classical mixed-integer programming solvers. Additionally, a local search heuristic is presented to calculate locally optimal networks. Furthermore to improve efficiency we present an iterative data-splitting heuristic which iteratively splits the training set into smaller subsets by using the k-mean method. Afterwards all data points in a given subset are forced to follow the same activation pattern, which leads to a much smaller number of integer variables in the mixed-integer programming formulation and therefore to computational improvements. Finally for the first time a robust model is presented which enforces robustness of the BDNN during training. All methods are tested on random and real datasets and our results indicate that all models can often compete with or even outperform classical DNNs on small network architectures confirming the viability for applications having restricted memory or computing power.

Towards the Localisation of Lesions in Diabetic Retinopathy

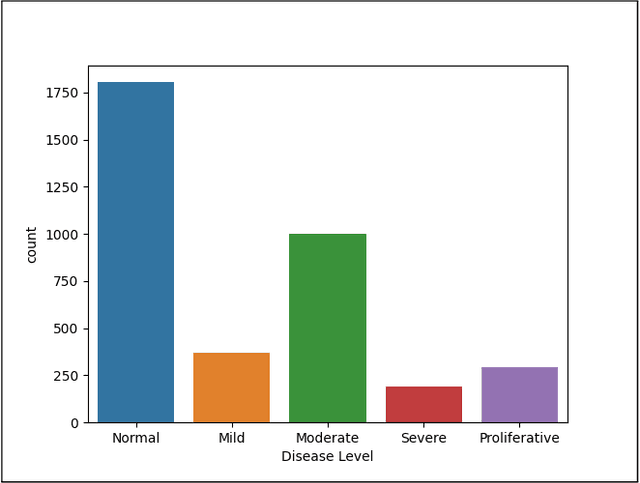
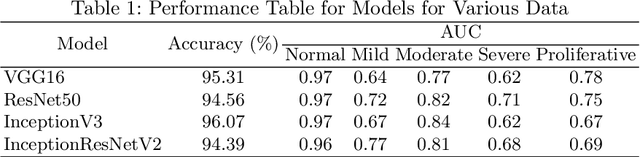
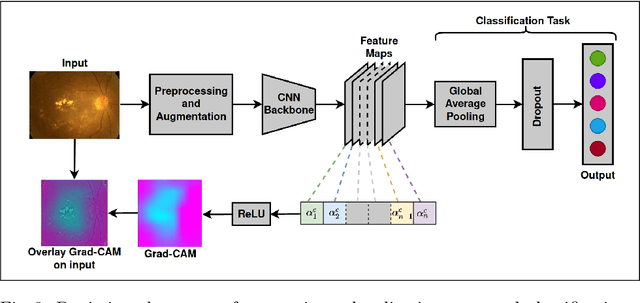
Convolutional Neural Networks (CNNs) have successfully been used to classify diabetic retinopathy (DR) fundus images in recent times. However, deeper representations in CNNs may capture higher-level semantics at the expense of spatial resolution. To make predictions usable for ophthalmologists, we use a post-attention technique called Gradient-weighted Class Activation Mapping (Grad-CAM) on the penultimate layer of deep learning models to produce coarse localisation maps on DR fundus images. This is to help identify discriminative regions in the images, consequently providing evidence for ophthalmologists to make a diagnosis and potentially save lives by early diagnosis. Specifically, this study uses pre-trained weights from four state-of-the-art deep learning models to produce and compare localisation maps of DR fundus images. The models used include VGG16, ResNet50, InceptionV3, and InceptionResNetV2. We find that InceptionV3 achieves the best performance with a test classification accuracy of 96.07%, and localise lesions better and faster than the other models.

An Integer Programming Approach to Deep Neural Networks with Binary Activation Functions

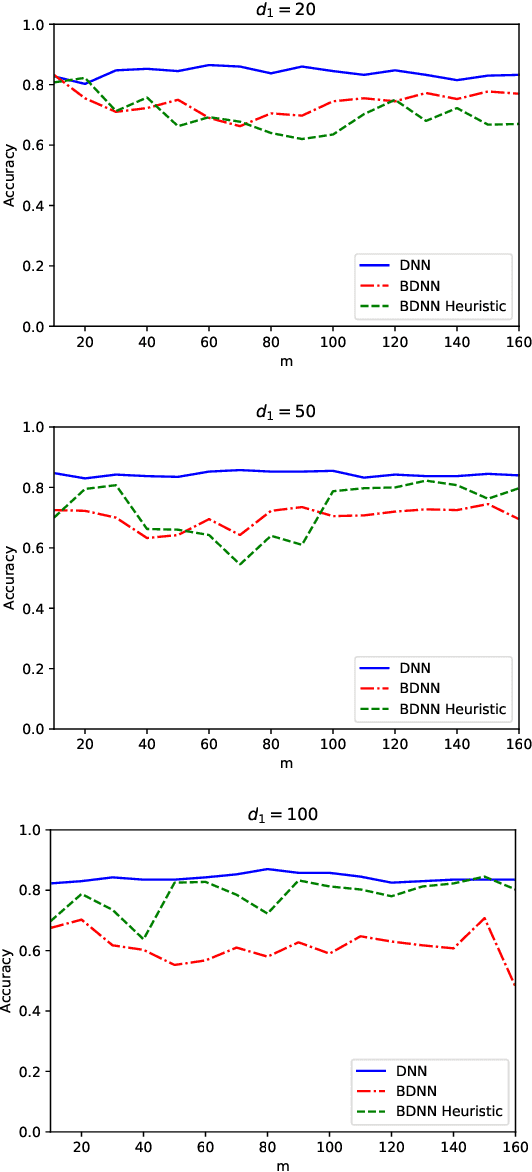
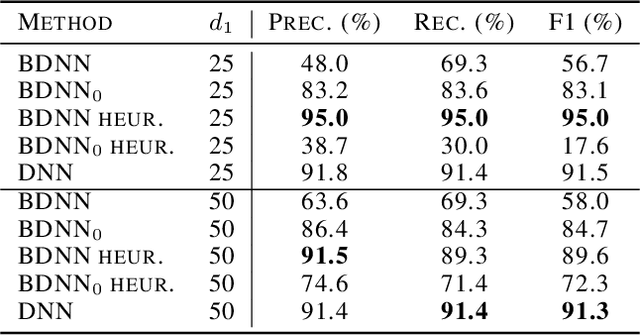
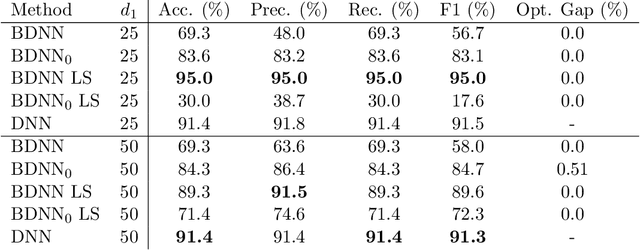
We study deep neural networks with binary activation functions (BDNN), i.e. the activation function only has two states. We show that the BDNN can be reformulated as a mixed-integer linear program which can be solved to global optimality by classical integer programming solvers. Additionally, a heuristic solution algorithm is presented and we study the model under data uncertainty, applying a two-stage robust optimization approach. We implemented our methods on random and real datasets and show that the heuristic version of the BDNN outperforms classical deep neural networks on the Breast Cancer Wisconsin dataset while performing worse on random data.

On Error Correction Neural Networks for Economic Forecasting

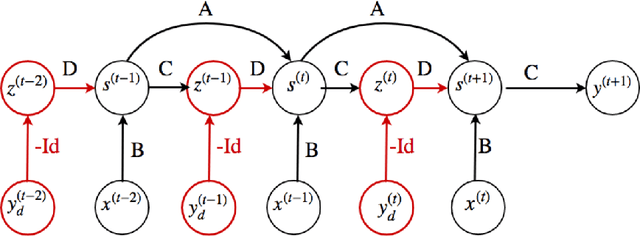
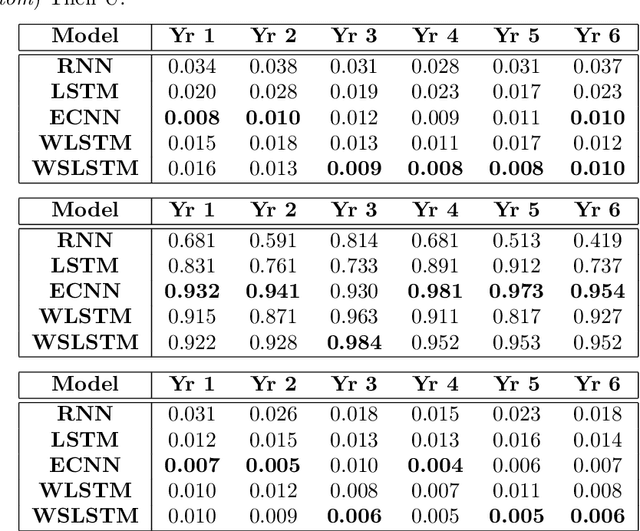
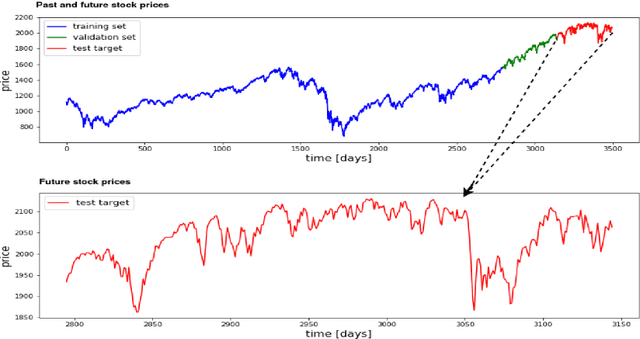
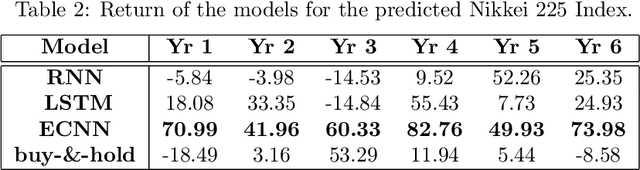
Recurrent neural networks (RNNs) are more suitable for learning non-linear dependencies in dynamical systems from observed time series data. In practice all the external variables driving such systems are not know a priori, especially in economical forecasting. A class of RNNs called Error Correction Neural Networks (ECNNs) was designed to compensate for missing input variables. It does this by feeding back in the current step the error made in the previous step. The ECNN is implemented in Python by the computation of the appropriate gradients and it is tested on stock market predictions. As expected it out performed the simple RNN and LSTM and other hybrid models which involve a de-noising pre-processing step. The intuition for the latter is that de-noising may lead to loss of information.

Learning deep linear neural networks: Riemannian gradient flows and convergence to global minimizers

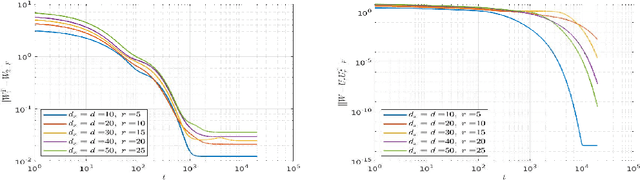
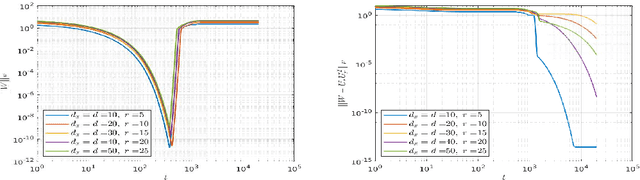
We study the convergence of gradient flows related to learning deep linear neural networks from data (i.e., the activation function is the identity map). In this case, the composition of the network layers amounts to simply multiplying the weight matrices of all layers together, resulting in an overparameterized problem. We show that the gradient flow with respect to these factors can be re-interpreted as a Riemannian gradient flow on the manifold of rank-$r$ matrices endowed with a suitable Riemannian metric. We show that the flow always converges to a critical point of the underlying functional. Moreover, in the special case of an autoencoder, we show that the flow converges to a global minimum for almost all initializations.

Convex block-sparse linear regression with expanders -- provably

Sparse matrices are favorable objects in machine learning and optimization. When such matrices are used, in place of dense ones, the overall complexity requirements in optimization can be significantly reduced in practice, both in terms of space and run-time. Prompted by this observation, we study a convex optimization scheme for block-sparse recovery from linear measurements. To obtain linear sketches, we use expander matrices, i.e., sparse matrices containing only few non-zeros per column. Hitherto, to the best of our knowledge, such algorithmic solutions have been only studied from a non-convex perspective. Our aim here is to theoretically characterize the performance of convex approaches under such setting. Our key novelty is the expression of the recovery error in terms of the model-based norm, while assuring that solution lives in the model. To achieve this, we show that sparse model-based matrices satisfy a group version of the null-space property. Our experimental findings on synthetic and real applications support our claims for faster recovery in the convex setting -- as opposed to using dense sensing matrices, while showing a competitive recovery performance.

Energy-aware adaptive bi-Lipschitz embeddings

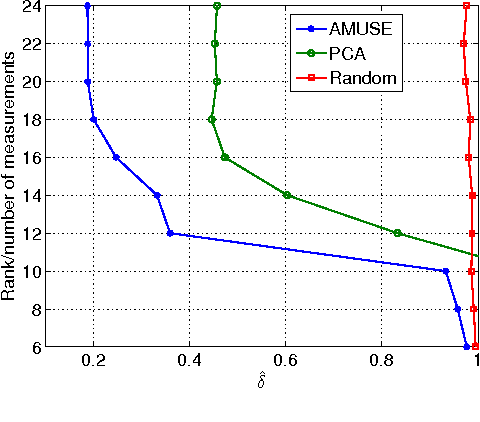
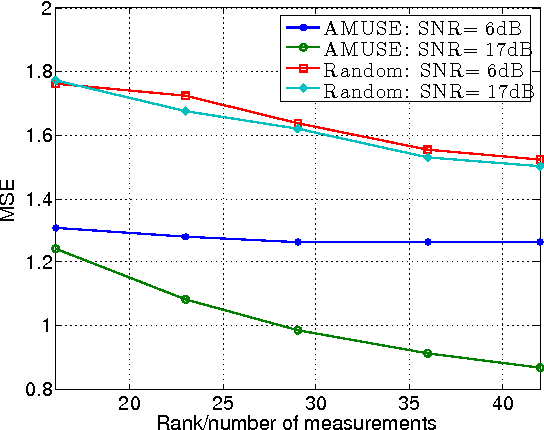
We propose a dimensionality reducing matrix design based on training data with constraints on its Frobenius norm and number of rows. Our design criteria is aimed at preserving the distances between the data points in the dimensionality reduced space as much as possible relative to their distances in original data space. This approach can be considered as a deterministic Bi-Lipschitz embedding of the data points. We introduce a scalable learning algorithm, dubbed AMUSE, and provide a rigorous estimation guarantee by leveraging game theoretic tools. We also provide a generalization characterization of our matrix based on our sample data. We use compressive sensing problems as an example application of our problem, where the Frobenius norm design constraint translates into the sensing energy.