Rouzbeh Hasheminezhad
Compressive Closeness in Networks
Jun 19, 2019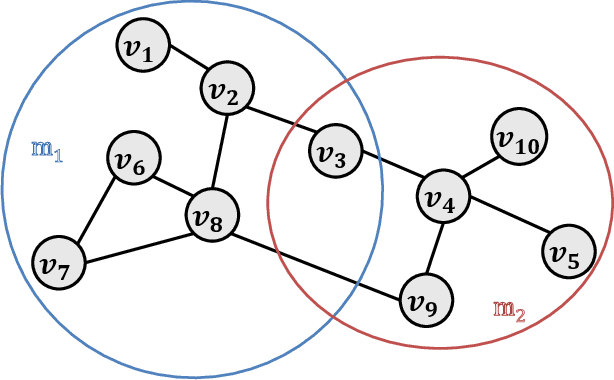
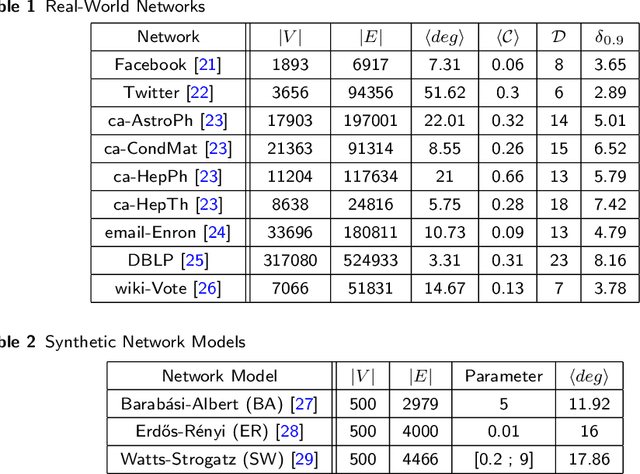
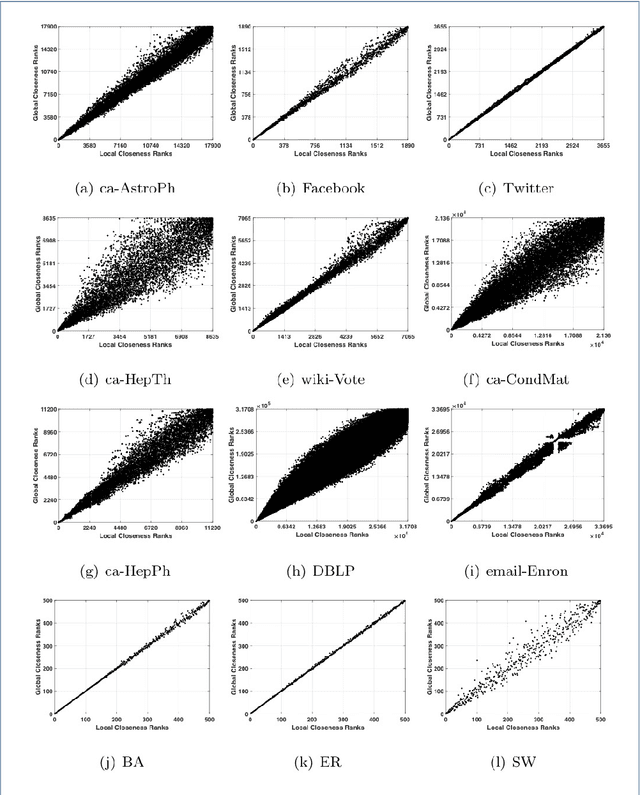
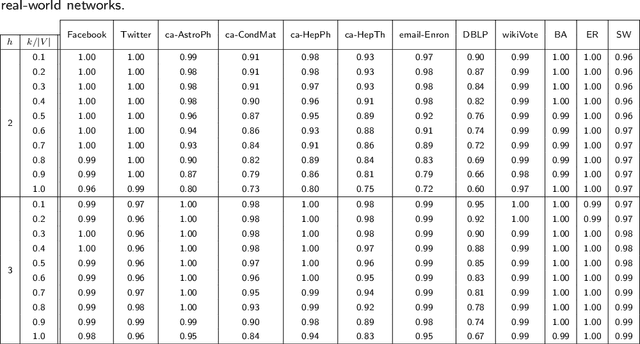
Abstract:Distributed algorithms for network science applications are of great importance due to today's large real-world networks. In such algorithms, a node is allowed only to have local interactions with its immediate neighbors. This is because the whole network topological structure is often unknown to each node. Recently, distributed detection of central nodes, concerning different notions of importance, within a network has received much attention. Closeness centrality is a prominent measure to evaluate the importance (influence) of nodes, based on their accessibility, in a given network. In this paper, first, we introduce a local (ego-centric) metric that correlates well with the global closeness centrality; however, it has very low computational complexity. Second, we propose a compressive sensing (CS)-based framework to accurately recover high closeness centrality nodes in the network utilizing the proposed local metric. Both ego-centric metric computation and its aggregation via CS are efficient and distributed, using only local interactions between neighboring nodes. Finally, we evaluate the performance of the proposed method through extensive experiments on various synthetic and real-world networks. The results show that the proposed local metric correlates with the global closeness centrality, better than the current local metrics. Moreover, the results demonstrate that the proposed CS-based method outperforms the state-of-the-art methods with notable improvement.
Convex block-sparse linear regression with expanders -- provably
Apr 03, 2016

Abstract:Sparse matrices are favorable objects in machine learning and optimization. When such matrices are used, in place of dense ones, the overall complexity requirements in optimization can be significantly reduced in practice, both in terms of space and run-time. Prompted by this observation, we study a convex optimization scheme for block-sparse recovery from linear measurements. To obtain linear sketches, we use expander matrices, i.e., sparse matrices containing only few non-zeros per column. Hitherto, to the best of our knowledge, such algorithmic solutions have been only studied from a non-convex perspective. Our aim here is to theoretically characterize the performance of convex approaches under such setting. Our key novelty is the expression of the recovery error in terms of the model-based norm, while assuring that solution lives in the model. To achieve this, we show that sparse model-based matrices satisfy a group version of the null-space property. Our experimental findings on synthetic and real applications support our claims for faster recovery in the convex setting -- as opposed to using dense sensing matrices, while showing a competitive recovery performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge