Convex block-sparse linear regression with expanders -- provably

Sparse matrices are favorable objects in machine learning and optimization. When such matrices are used, in place of dense ones, the overall complexity requirements in optimization can be significantly reduced in practice, both in terms of space and run-time. Prompted by this observation, we study a convex optimization scheme for block-sparse recovery from linear measurements. To obtain linear sketches, we use expander matrices, i.e., sparse matrices containing only few non-zeros per column. Hitherto, to the best of our knowledge, such algorithmic solutions have been only studied from a non-convex perspective. Our aim here is to theoretically characterize the performance of convex approaches under such setting. Our key novelty is the expression of the recovery error in terms of the model-based norm, while assuring that solution lives in the model. To achieve this, we show that sparse model-based matrices satisfy a group version of the null-space property. Our experimental findings on synthetic and real applications support our claims for faster recovery in the convex setting -- as opposed to using dense sensing matrices, while showing a competitive recovery performance.

Learning-based Compressive Subsampling

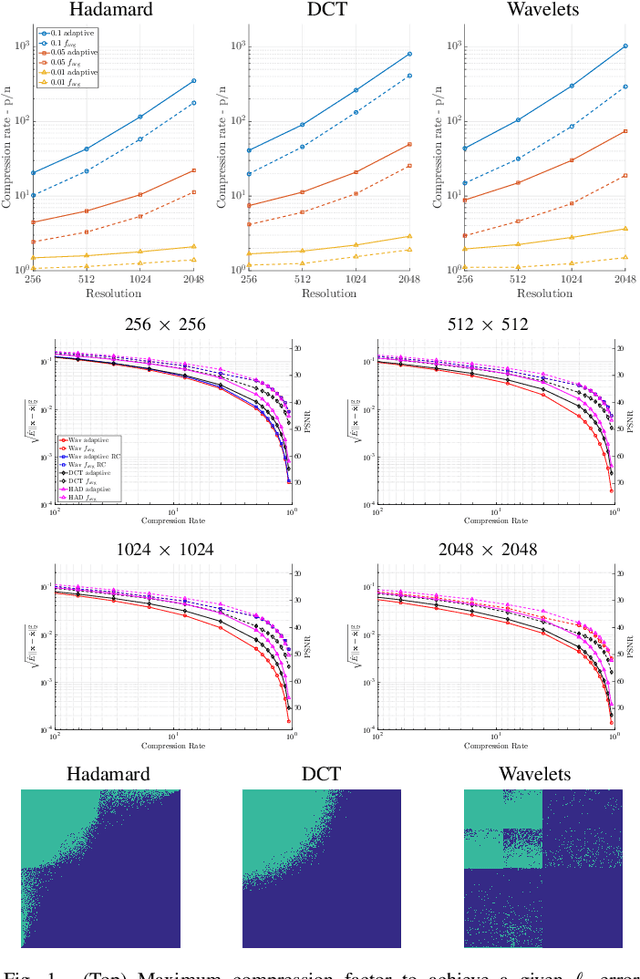
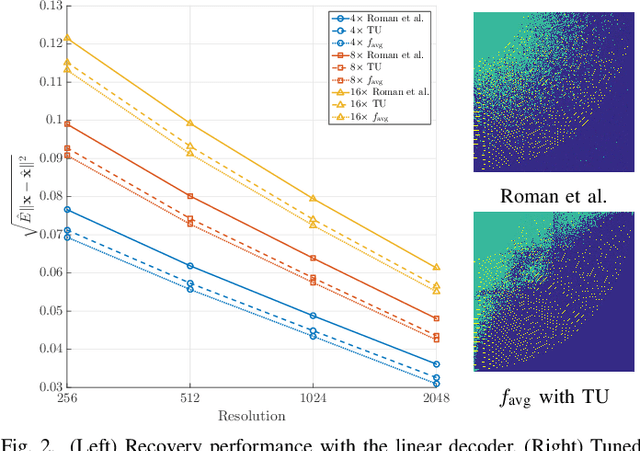
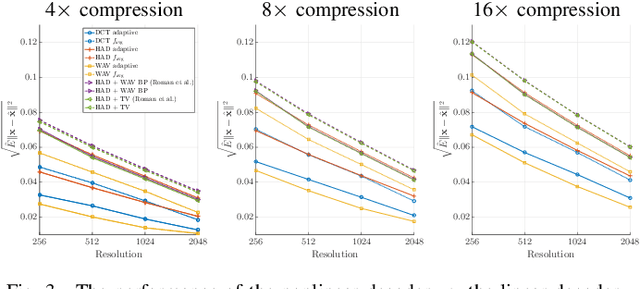
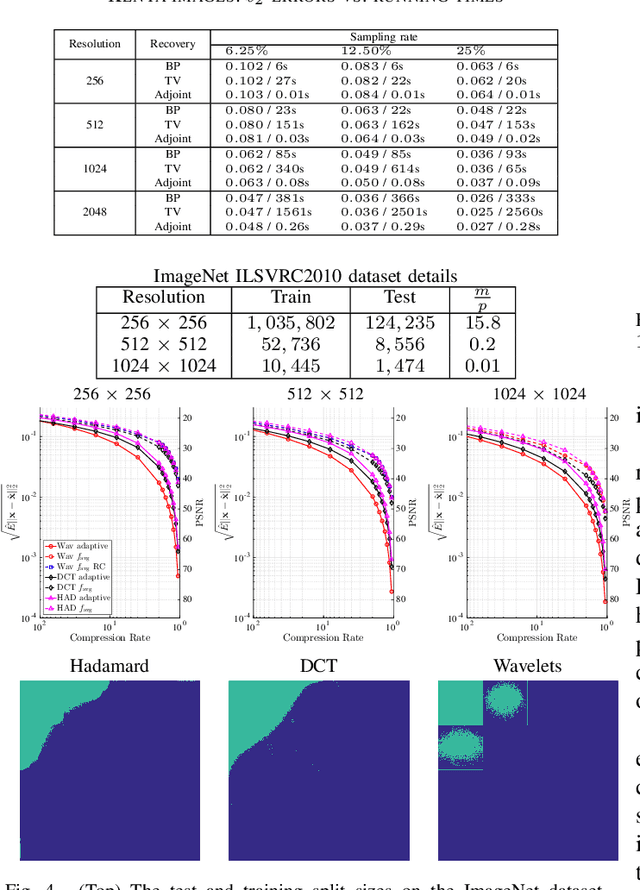
The problem of recovering a structured signal $\mathbf{x} \in \mathbb{C}^p$ from a set of dimensionality-reduced linear measurements $\mathbf{b} = \mathbf {A}\mathbf {x}$ arises in a variety of applications, such as medical imaging, spectroscopy, Fourier optics, and computerized tomography. Due to computational and storage complexity or physical constraints imposed by the problem, the measurement matrix $\mathbf{A} \in \mathbb{C}^{n \times p}$ is often of the form $\mathbf{A} = \mathbf{P}_{\Omega}\boldsymbol{\Psi}$ for some orthonormal basis matrix $\boldsymbol{\Psi}\in \mathbb{C}^{p \times p}$ and subsampling operator $\mathbf{P}_{\Omega}: \mathbb{C}^{p} \rightarrow \mathbb{C}^{n}$ that selects the rows indexed by $\Omega$. This raises the fundamental question of how best to choose the index set $\Omega$ in order to optimize the recovery performance. Previous approaches to addressing this question rely on non-uniform \emph{random} subsampling using application-specific knowledge of the structure of $\mathbf{x}$. In this paper, we instead take a principled learning-based approach in which a \emph{fixed} index set is chosen based on a set of training signals $\mathbf{x}_1,\dotsc,\mathbf{x}_m$. We formulate combinatorial optimization problems seeking to maximize the energy captured in these signals in an average-case or worst-case sense, and we show that these can be efficiently solved either exactly or approximately via the identification of modularity and submodularity structures. We provide both deterministic and statistical theoretical guarantees showing how the resulting measurement matrices perform on signals differing from the training signals, and we provide numerical examples showing our approach to be effective on a variety of data sets.

Structured Sparsity: Discrete and Convex approaches

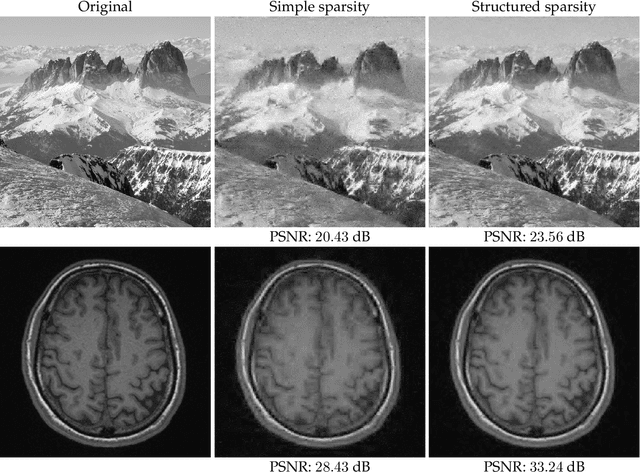
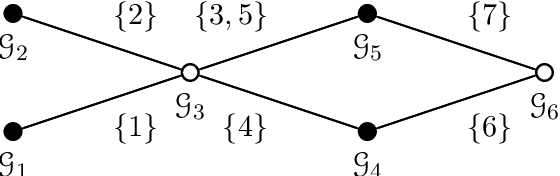
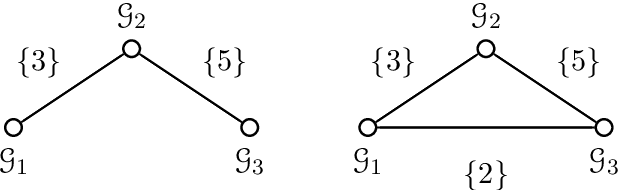
Compressive sensing (CS) exploits sparsity to recover sparse or compressible signals from dimensionality reducing, non-adaptive sensing mechanisms. Sparsity is also used to enhance interpretability in machine learning and statistics applications: While the ambient dimension is vast in modern data analysis problems, the relevant information therein typically resides in a much lower dimensional space. However, many solutions proposed nowadays do not leverage the true underlying structure. Recent results in CS extend the simple sparsity idea to more sophisticated {\em structured} sparsity models, which describe the interdependency between the nonzero components of a signal, allowing to increase the interpretability of the results and lead to better recovery performance. In order to better understand the impact of structured sparsity, in this chapter we analyze the connections between the discrete models and their convex relaxations, highlighting their relative advantages. We start with the general group sparse model and then elaborate on two important special cases: the dispersive and the hierarchical models. For each, we present the models in their discrete nature, discuss how to solve the ensuing discrete problems and then describe convex relaxations. We also consider more general structures as defined by set functions and present their convex proxies. Further, we discuss efficient optimization solutions for structured sparsity problems and illustrate structured sparsity in action via three applications.

Group-Sparse Model Selection: Hardness and Relaxations

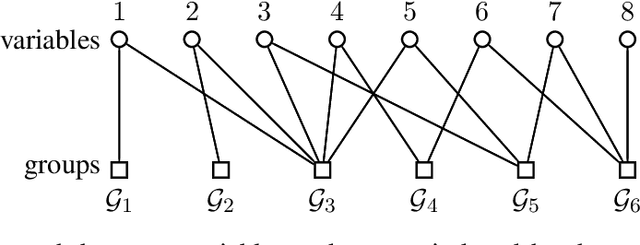
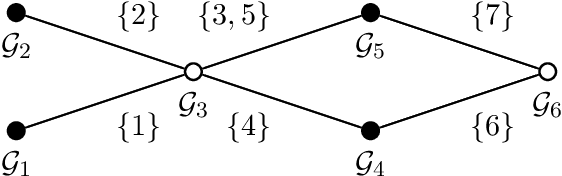
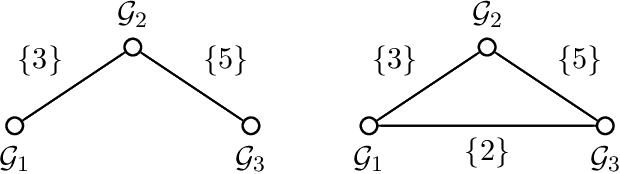
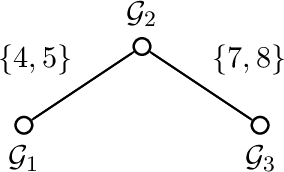
Group-based sparsity models are proven instrumental in linear regression problems for recovering signals from much fewer measurements than standard compressive sensing. The main promise of these models is the recovery of "interpretable" signals through the identification of their constituent groups. In this paper, we establish a combinatorial framework for group-model selection problems and highlight the underlying tractability issues. In particular, we show that the group-model selection problem is equivalent to the well-known NP-hard weighted maximum coverage problem (WMC). Leveraging a graph-based understanding of group models, we describe group structures which enable correct model selection in polynomial time via dynamic programming. Furthermore, group structures that lead to totally unimodular constraints have tractable discrete as well as convex relaxations. We also present a generalization of the group-model that allows for within group sparsity, which can be used to model hierarchical sparsity. Finally, we study the Pareto frontier of group-sparse approximations for two tractable models, among which the tree sparsity model, and illustrate selection and computation trade-offs between our framework and the existing convex relaxations.

On Sparsity Inducing Regularization Methods for Machine Learning

During the past years there has been an explosion of interest in learning methods based on sparsity regularization. In this paper, we discuss a general class of such methods, in which the regularizer can be expressed as the composition of a convex function $\omega$ with a linear function. This setting includes several methods such the group Lasso, the Fused Lasso, multi-task learning and many more. We present a general approach for solving regularization problems of this kind, under the assumption that the proximity operator of the function $\omega$ is available. Furthermore, we comment on the application of this approach to support vector machines, a technique pioneered by the groundbreaking work of Vladimir Vapnik.

Optimal Computational Trade-Off of Inexact Proximal Methods

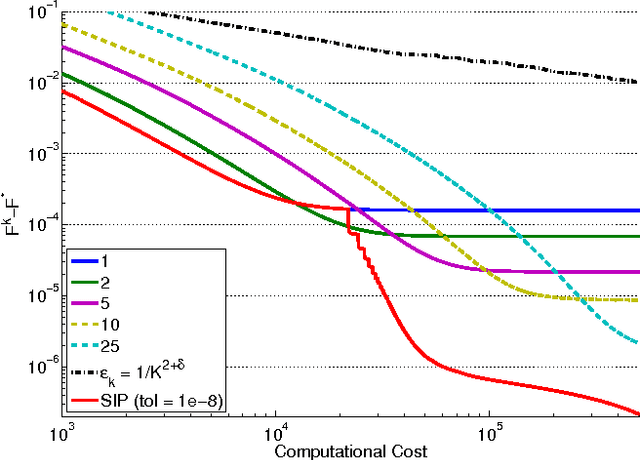
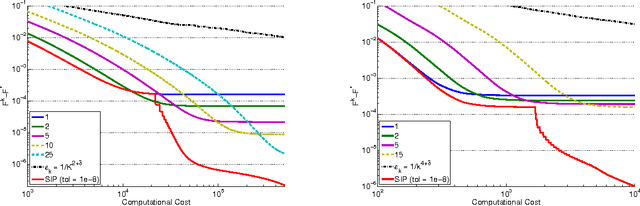
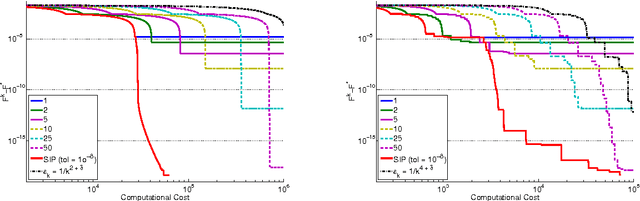
In this paper, we investigate the trade-off between convergence rate and computational cost when minimizing a composite functional with proximal-gradient methods, which are popular optimisation tools in machine learning. We consider the case when the proximity operator is computed via an iterative procedure, which provides an approximation of the exact proximity operator. In that case, we obtain algorithms with two nested loops. We show that the strategy that minimizes the computational cost to reach a solution with a desired accuracy in finite time is to set the number of inner iterations to a constant, which differs from the strategy indicated by a convergence rate analysis. In the process, we also present a new procedure called SIP (that is Speedy Inexact Proximal-gradient algorithm) that is both computationally efficient and easy to implement. Our numerical experiments confirm the theoretical findings and suggest that SIP can be a very competitive alternative to the standard procedure.

Modeling transition dynamics in MDPs with RKHS embeddings of conditional distributions

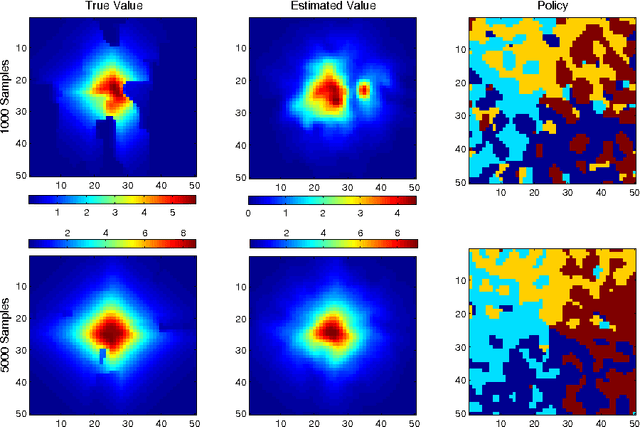
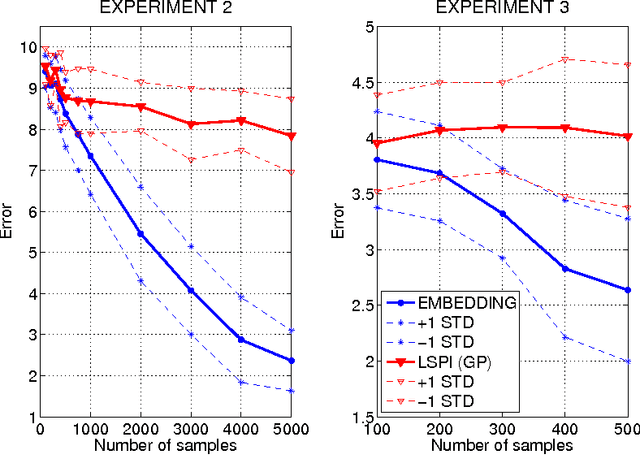
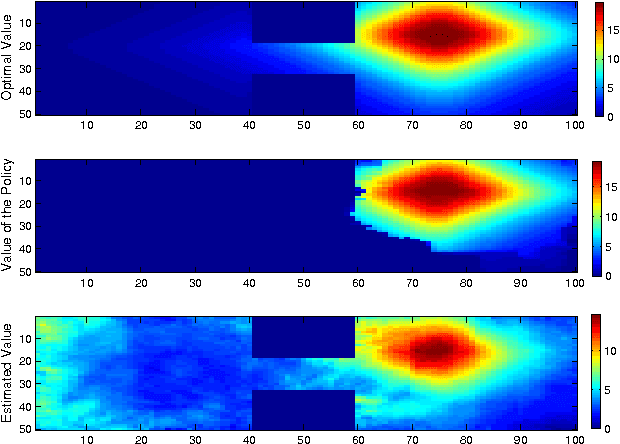
We propose a new, nonparametric approach to estimating the value function in reinforcement learning. This approach makes use of a recently developed representation of conditional distributions as functions in a reproducing kernel Hilbert space. Such representations bypass the need for estimating transition probabilities, and apply to any domain on which kernels can be defined. Our approach avoids the need to approximate intractable integrals since expectations are represented as RKHS inner products whose computation has linear complexity in the sample size. Thus, we can efficiently perform value function estimation in a wide variety of settings, including finite state spaces, continuous states spaces, and partially observable tasks where only sensor measurements are available. A second advantage of the approach is that we learn the conditional distribution representation from a training sample, and do not require an exhaustive exploration of the state space. We prove convergence of our approach either to the optimal policy, or to the closest projection of the optimal policy in our model class, under reasonable assumptions. In experiments, we demonstrate the performance of our algorithm on a learning task in a continuous state space (the under-actuated pendulum), and on a navigation problem where only images from a sensor are observed. We compare with least-squares policy iteration where a Gaussian process is used for value function estimation. Our algorithm achieves better performance in both tasks.

Conditional mean embeddings as regressors - supplementary

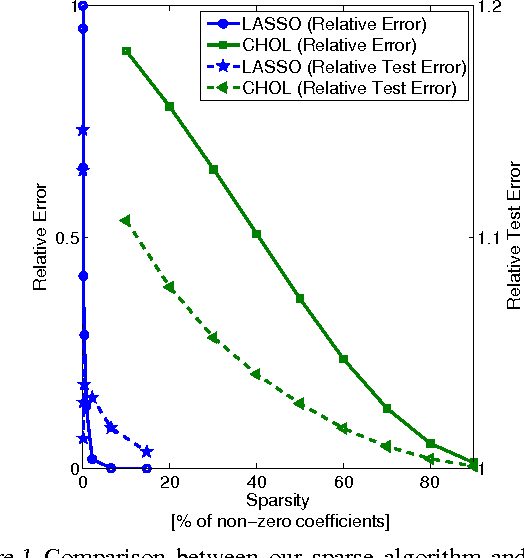
We demonstrate an equivalence between reproducing kernel Hilbert space (RKHS) embeddings of conditional distributions and vector-valued regressors. This connection introduces a natural regularized loss function which the RKHS embeddings minimise, providing an intuitive understanding of the embeddings and a justification for their use. Furthermore, the equivalence allows the application of vector-valued regression methods and results to the problem of learning conditional distributions. Using this link we derive a sparse version of the embedding by considering alternative formulations. Further, by applying convergence results for vector-valued regression to the embedding problem we derive minimax convergence rates which are O(\log(n)/n) -- compared to current state of the art rates of O(n^{-1/4}) -- and are valid under milder and more intuitive assumptions. These minimax upper rates coincide with lower rates up to a logarithmic factor, showing that the embedding method achieves nearly optimal rates. We study our sparse embedding algorithm in a reinforcement learning task where the algorithm shows significant improvement in sparsity over an incomplete Cholesky decomposition.

Modelling transition dynamics in MDPs with RKHS embeddings

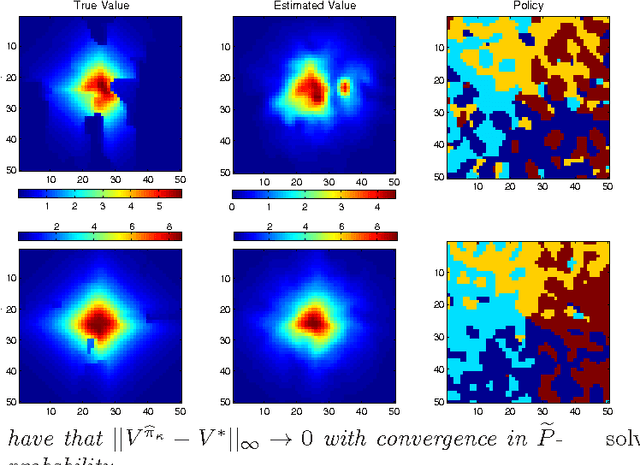
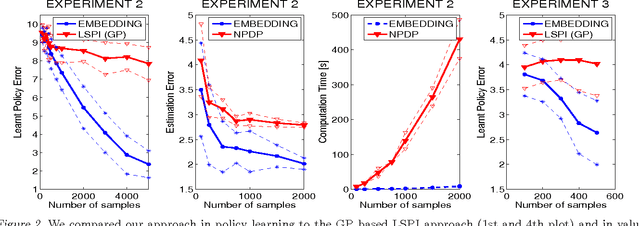
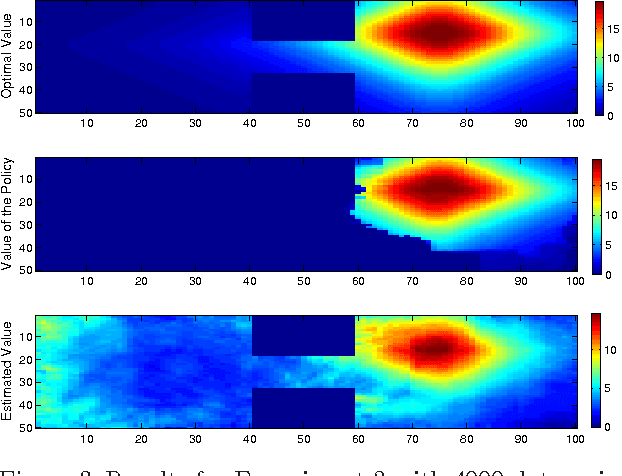
We propose a new, nonparametric approach to learning and representing transition dynamics in Markov decision processes (MDPs), which can be combined easily with dynamic programming methods for policy optimisation and value estimation. This approach makes use of a recently developed representation of conditional distributions as \emph{embeddings} in a reproducing kernel Hilbert space (RKHS). Such representations bypass the need for estimating transition probabilities or densities, and apply to any domain on which kernels can be defined. This avoids the need to calculate intractable integrals, since expectations are represented as RKHS inner products whose computation has linear complexity in the number of points used to represent the embedding. We provide guarantees for the proposed applications in MDPs: in the context of a value iteration algorithm, we prove convergence to either the optimal policy, or to the closest projection of the optimal policy in our model class (an RKHS), under reasonable assumptions. In experiments, we investigate a learning task in a typical classical control setting (the under-actuated pendulum), and on a navigation problem where only images from a sensor are observed. For policy optimisation we compare with least-squares policy iteration where a Gaussian process is used for value function estimation. For value estimation we also compare to the NPDP method. Our approach achieves better performance in all experiments.

A General Framework for Structured Sparsity via Proximal Optimization

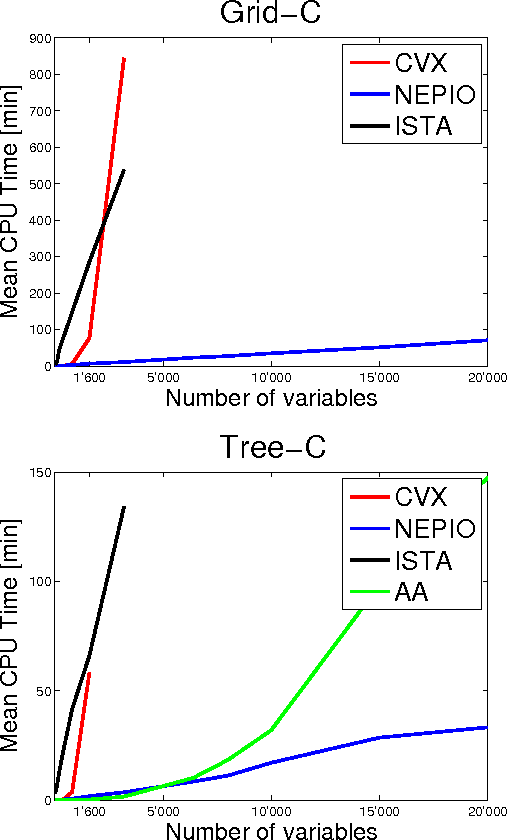
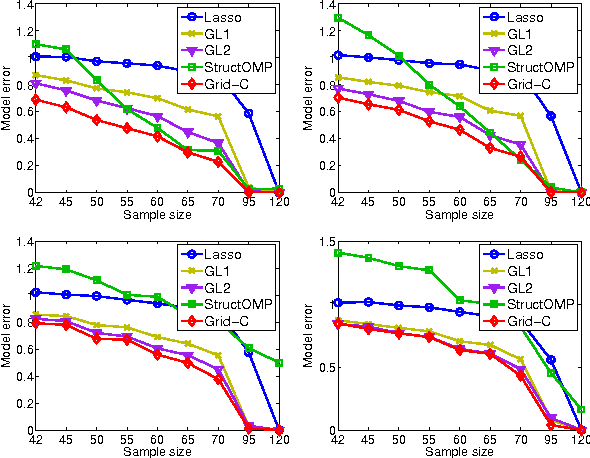
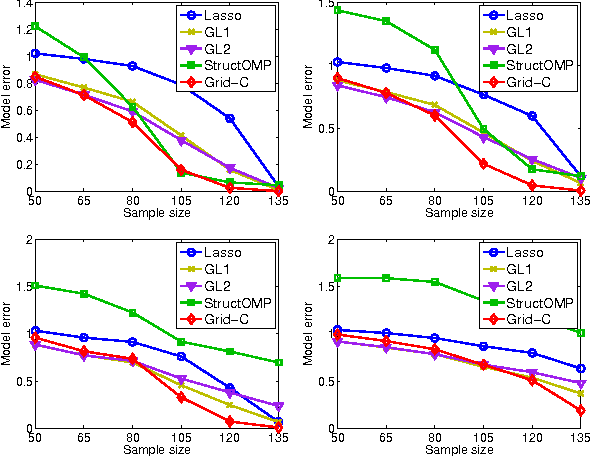
We study a generalized framework for structured sparsity. It extends the well-known methods of Lasso and Group Lasso by incorporating additional constraints on the variables as part of a convex optimization problem. This framework provides a straightforward way of favouring prescribed sparsity patterns, such as orderings, contiguous regions and overlapping groups, among others. Existing optimization methods are limited to specific constraint sets and tend to not scale well with sample size and dimensionality. We propose a novel first order proximal method, which builds upon results on fixed points and successive approximations. The algorithm can be applied to a general class of conic and norm constraints sets and relies on a proximity operator subproblem which can be computed explicitly. Experiments on different regression problems demonstrate the efficiency of the optimization algorithm and its scalability with the size of the problem. They also demonstrate state of the art statistical performance, which improves over Lasso and StructOMP.