Jean Morales
A General Framework for Structured Sparsity via Proximal Optimization
Jun 26, 2011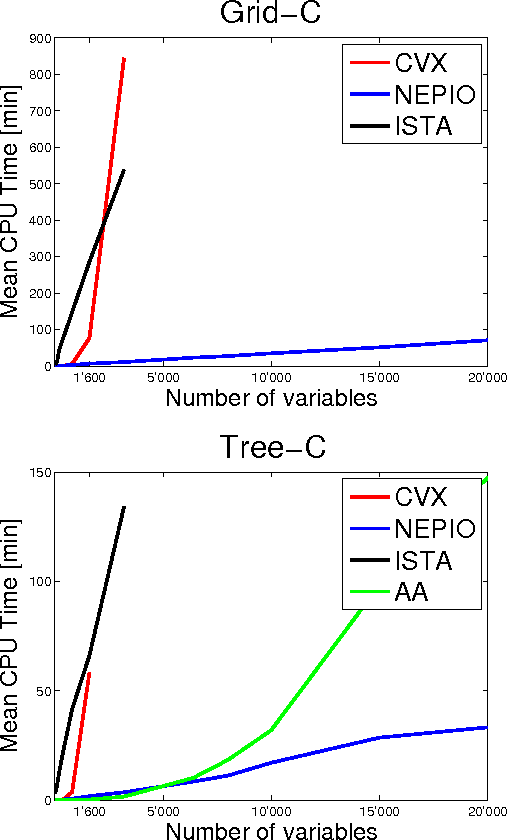
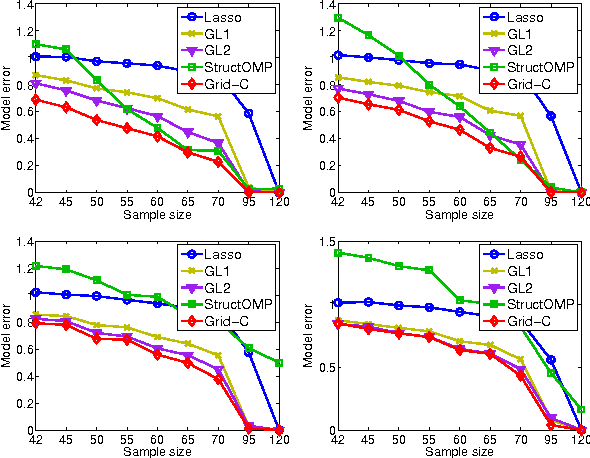
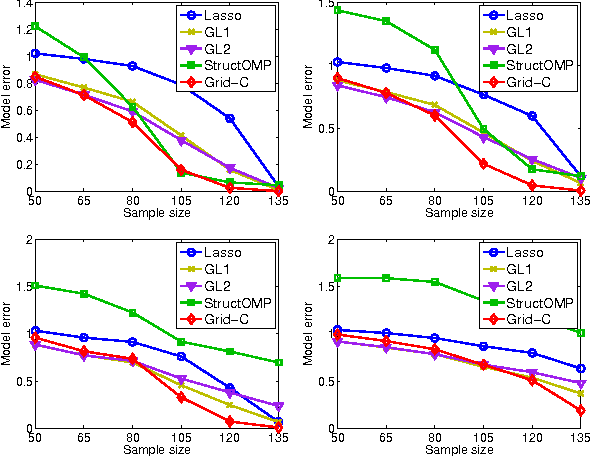

Abstract:We study a generalized framework for structured sparsity. It extends the well-known methods of Lasso and Group Lasso by incorporating additional constraints on the variables as part of a convex optimization problem. This framework provides a straightforward way of favouring prescribed sparsity patterns, such as orderings, contiguous regions and overlapping groups, among others. Existing optimization methods are limited to specific constraint sets and tend to not scale well with sample size and dimensionality. We propose a novel first order proximal method, which builds upon results on fixed points and successive approximations. The algorithm can be applied to a general class of conic and norm constraints sets and relies on a proximity operator subproblem which can be computed explicitly. Experiments on different regression problems demonstrate the efficiency of the optimization algorithm and its scalability with the size of the problem. They also demonstrate state of the art statistical performance, which improves over Lasso and StructOMP.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge