Approximations of the Restless Bandit Problem

The multi-armed restless bandit problem is studied in the case where the pay-off distributions are stationary $\varphi$-mixing. This version of the problem provides a more realistic model for most real-world applications, but cannot be optimally solved in practice, since it is known to be PSPACE-hard. The objective of this paper is to characterize a sub-class of the problem where {\em good} approximate solutions can be found using tractable approaches. Specifically, it is shown that under some conditions on the $\varphi$-mixing coefficients, a modified version of UCB can prove effective. The main challenge is that, unlike in the i.i.d. setting, the distributions of the sampled pay-offs may not have the same characteristics as those of the original bandit arms. In particular, the $\varphi$-mixing property does not necessarily carry over. This is overcome by carefully controlling the effect of a sampling policy on the pay-off distributions. Some of the proof techniques developed in this paper can be more generally used in the context of online sampling under dependence. Proposed algorithms are accompanied with corresponding regret analysis.

Bandits with Delayed, Aggregated Anonymous Feedback

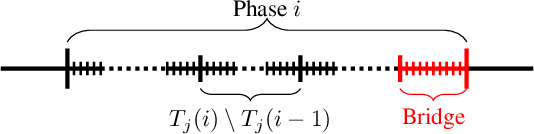
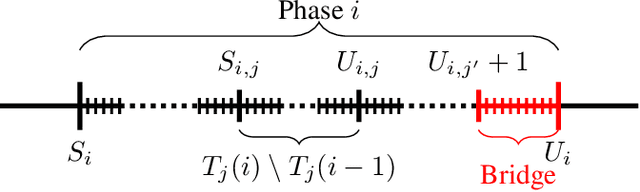
We study a variant of the stochastic $K$-armed bandit problem, which we call "bandits with delayed, aggregated anonymous feedback". In this problem, when the player pulls an arm, a reward is generated, however it is not immediately observed. Instead, at the end of each round the player observes only the sum of a number of previously generated rewards which happen to arrive in the given round. The rewards are stochastically delayed and due to the aggregated nature of the observations, the information of which arm led to a particular reward is lost. The question is what is the cost of the information loss due to this delayed, aggregated anonymous feedback? Previous works have studied bandits with stochastic, non-anonymous delays and found that the regret increases only by an additive factor relating to the expected delay. In this paper, we show that this additive regret increase can be maintained in the harder delayed, aggregated anonymous feedback setting when the expected delay (or a bound on it) is known. We provide an algorithm that matches the worst case regret of the non-anonymous problem exactly when the delays are bounded, and up to logarithmic factors or an additive variance term for unbounded delays.

Modelling transition dynamics in MDPs with RKHS embeddings

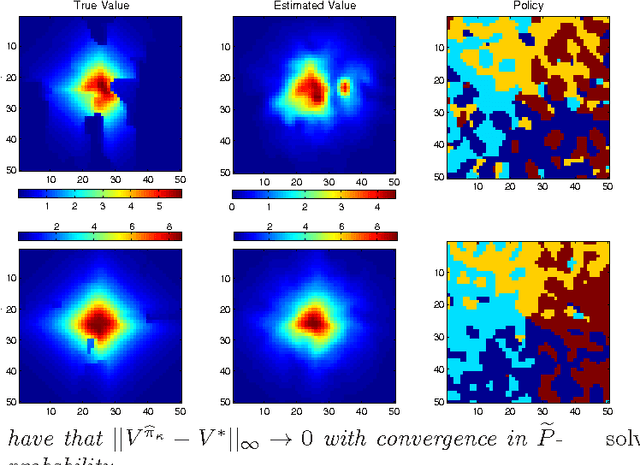
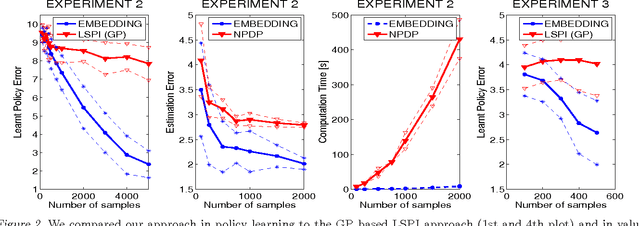
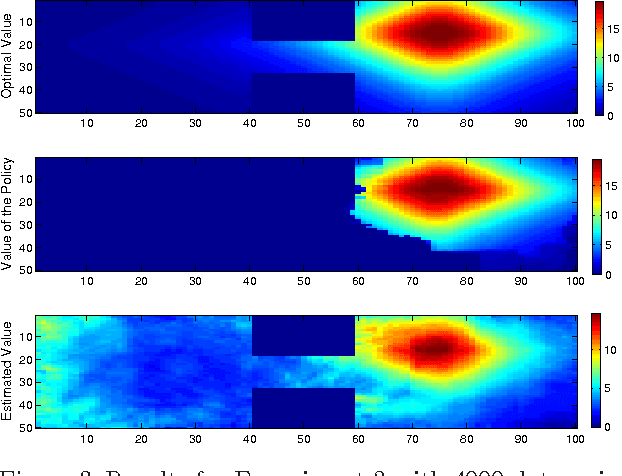
We propose a new, nonparametric approach to learning and representing transition dynamics in Markov decision processes (MDPs), which can be combined easily with dynamic programming methods for policy optimisation and value estimation. This approach makes use of a recently developed representation of conditional distributions as \emph{embeddings} in a reproducing kernel Hilbert space (RKHS). Such representations bypass the need for estimating transition probabilities or densities, and apply to any domain on which kernels can be defined. This avoids the need to calculate intractable integrals, since expectations are represented as RKHS inner products whose computation has linear complexity in the number of points used to represent the embedding. We provide guarantees for the proposed applications in MDPs: in the context of a value iteration algorithm, we prove convergence to either the optimal policy, or to the closest projection of the optimal policy in our model class (an RKHS), under reasonable assumptions. In experiments, we investigate a learning task in a typical classical control setting (the under-actuated pendulum), and on a navigation problem where only images from a sensor are observed. For policy optimisation we compare with least-squares policy iteration where a Gaussian process is used for value function estimation. For value estimation we also compare to the NPDP method. Our approach achieves better performance in all experiments.