Restless Linear Bandits

A more general formulation of the linear bandit problem is considered to allow for dependencies over time. Specifically, it is assumed that there exists an unknown $\mathbb{R}^d$-valued stationary $\varphi$-mixing sequence of parameters $(\theta_t,~t \in \mathbb{N})$ which gives rise to pay-offs. This instance of the problem can be viewed as a generalization of both the classical linear bandits with iid noise, and the finite-armed restless bandits. In light of the well-known computational hardness of optimal policies for restless bandits, an approximation is proposed whose error is shown to be controlled by the $\varphi$-dependence between consecutive $\theta_t$. An optimistic algorithm, called LinMix-UCB, is proposed for the case where $\theta_t$ has an exponential mixing rate. The proposed algorithm is shown to incur a sub-linear regret of $\mathcal{O}\left(\sqrt{d n\mathrm{polylog}(n) }\right)$ with respect to an oracle that always plays a multiple of $\mathbb{E}\theta_t$. The main challenge in this setting is to ensure that the exploration-exploitation strategy is robust against long-range dependencies. The proposed method relies on Berbee's coupling lemma to carefully select near-independent samples and construct confidence ellipsoids around empirical estimates of $\mathbb{E}\theta_t$.

Estimating the Mixing Coefficients of Geometrically Ergodic Markov Processes

We propose methods to estimate the individual $\beta$-mixing coefficients of a real-valued geometrically ergodic Markov process from a single sample-path $X_0,X_1, \dots,X_n$. Under standard smoothness conditions on the densities, namely, that the joint density of the pair $(X_0,X_m)$ for each $m$ lies in a Besov space $B^s_{1,\infty}(\mathbb R^2)$ for some known $s>0$, we obtain a rate of convergence of order $\mathcal{O}(\log(n) n^{-[s]/(2[s]+2)})$ for the expected error of our estimator in this case\footnote{We use $[s]$ to denote the integer part of the decomposition $s=[s]+\{s\}$ of $s \in (0,\infty)$ into an integer term and a {\em strictly positive} remainder term $\{s\} \in (0,1]$.}. We complement this result with a high-probability bound on the estimation error, and further obtain analogues of these bounds in the case where the state-space is finite. Naturally no density assumptions are required in this setting; the expected error rate is shown to be of order $\mathcal O(\log(n) n^{-1/2})$.

PyChEst: a Python package for the consistent retrospective estimation of distributional changes in piece-wise stationary time series

We introduce PyChEst, a Python package which provides tools for the simultaneous estimation of multiple changepoints in the distribution of piece-wise stationary time series. The nonparametric algorithms implemented are provably consistent in a general framework: when the samples are generated by unknown piece-wise stationary processes. In this setting, samples may have long-range dependencies of arbitrary form and the finite-dimensional marginals of any (unknown) fixed size before and after the changepoints may be the same. The strength of the algorithms included in the package is in their ability to consistently detect the changes without imposing any assumptions beyond stationarity on the underlying process distributions. We illustrate this distinguishing feature by comparing the performance of the package against state-of-the-art models designed for a setting where the samples are independently and identically distributed.

Oblivious Data for Fairness with Kernels

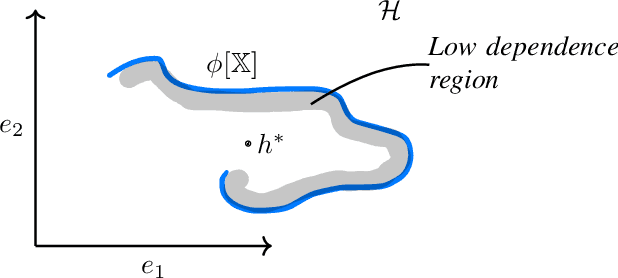
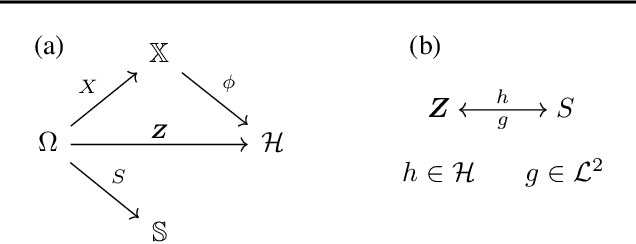
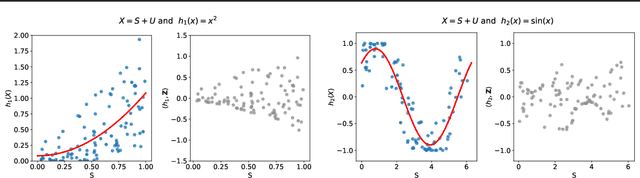
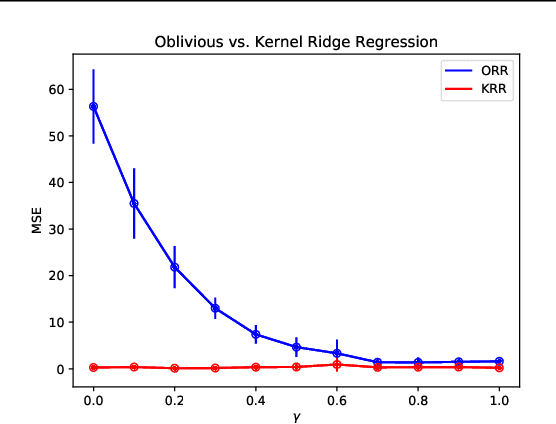
We investigate the problem of algorithmic fairness in the case where sensitive and non-sensitive features are available and one aims to generate new, `oblivious', features that closely approximate the non-sensitive features, and are only minimally dependent on the sensitive ones. We study this question in the context of kernel methods. We analyze a relaxed version of the Maximum Mean Discrepancy criterion which does not guarantee full independence but makes the optimization problem tractable. We derive a closed-form solution for this relaxed optimization problem and complement the result with a study of the dependencies between the newly generated features and the sensitive ones. Our key ingredient for generating such oblivious features is a Hilbert-space-valued conditional expectation, which needs to be estimated from data. We propose a plug-in approach and demonstrate how the estimation errors can be controlled. Our theoretical results are accompanied by experimental evaluations.

Clustering piecewise stationary processes

The problem of time-series clustering is considered in the case where each data-point is a sample generated by a piecewise stationary ergodic process. Stationary processes are perhaps the most general class of processes considered in non-parametric statistics and allow for arbitrary long-range dependence between variables. Piecewise stationary processes studied here for the first time in the context of clustering, relax the last remaining assumption in this model: stationarity. A natural formulation is proposed for this problem and a notion of consistency is introduced which requires the samples to be placed in the same cluster if and only if the piecewise stationary distributions that generate them have the same set of stationary distributions. Simple, computationally efficient algorithms are proposed and are shown to be consistent without any additional assumptions beyond piecewise stationarity.

Approximations of the Restless Bandit Problem

The multi-armed restless bandit problem is studied in the case where the pay-off distributions are stationary $\varphi$-mixing. This version of the problem provides a more realistic model for most real-world applications, but cannot be optimally solved in practice, since it is known to be PSPACE-hard. The objective of this paper is to characterize a sub-class of the problem where {\em good} approximate solutions can be found using tractable approaches. Specifically, it is shown that under some conditions on the $\varphi$-mixing coefficients, a modified version of UCB can prove effective. The main challenge is that, unlike in the i.i.d. setting, the distributions of the sampled pay-offs may not have the same characteristics as those of the original bandit arms. In particular, the $\varphi$-mixing property does not necessarily carry over. This is overcome by carefully controlling the effect of a sampling policy on the pay-off distributions. Some of the proof techniques developed in this paper can be more generally used in the context of online sampling under dependence. Proposed algorithms are accompanied with corresponding regret analysis.

Multiple Change Point Estimation in Stationary Ergodic Time Series

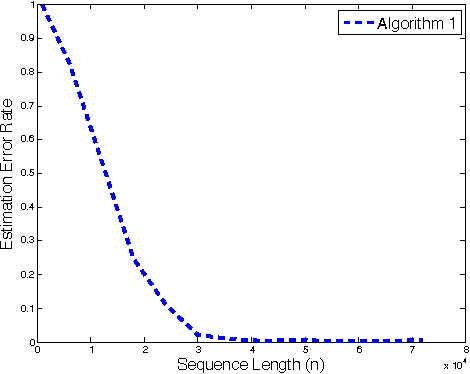
Given a heterogeneous time-series sample, the objective is to find points in time (called change points) where the probability distribution generating the data has changed. The data are assumed to have been generated by arbitrary unknown stationary ergodic distributions. No modelling, independence or mixing assumptions are made. A novel, computationally efficient, nonparametric method is proposed, and is shown to be asymptotically consistent in this general framework. The theoretical results are complemented with experimental evaluations.