Universal time-series forecasting with mixture predictors

This book is devoted to the problem of sequential probability forecasting, that is, predicting the probabilities of the next outcome of a growing sequence of observations given the past. This problem is considered in a very general setting that unifies commonly used probabilistic and non-probabilistic settings, trying to make as few as possible assumptions on the mechanism generating the observations. A common form that arises in various formulations of this problem is that of mixture predictors, which are formed as a combination of a finite or infinite set of other predictors attempting to combine their predictive powers. The main subject of this book are such mixture predictors, and the main results demonstrate the universality of this method in a very general probabilistic setting, but also show some of its limitations. While the problems considered are motivated by practical applications, involving, for example, financial, biological or behavioural data, this motivation is left implicit and all the results exposed are theoretical. The book targets graduate students and researchers interested in the problem of sequential prediction, and, more generally, in theoretical analysis of problems in machine learning and non-parametric statistics, as well as mathematical and philosophical foundations of these fields. The material in this volume is presented in a way that presumes familiarity with basic concepts of probability and statistics, up to and including probability distributions over spaces of infinite sequences. Familiarity with the literature on learning or stochastic processes is not required.

Clustering piecewise stationary processes

The problem of time-series clustering is considered in the case where each data-point is a sample generated by a piecewise stationary ergodic process. Stationary processes are perhaps the most general class of processes considered in non-parametric statistics and allow for arbitrary long-range dependence between variables. Piecewise stationary processes studied here for the first time in the context of clustering, relax the last remaining assumption in this model: stationarity. A natural formulation is proposed for this problem and a notion of consistency is introduced which requires the samples to be placed in the same cluster if and only if the piecewise stationary distributions that generate them have the same set of stationary distributions. Simple, computationally efficient algorithms are proposed and are shown to be consistent without any additional assumptions beyond piecewise stationarity.

Asymptotic nonparametric statistical analysis of stationary time series

Stationarity is a very general, qualitative assumption, that can be assessed on the basis of application specifics. It is thus a rather attractive assumption to base statistical analysis on, especially for problems for which less general qualitative assumptions, such as independence or finite memory, clearly fail. However, it has long been considered too general to allow for statistical inference to be made. One of the reasons for this is that rates of convergence, even of frequencies to the mean, are not available under this assumption alone. Recently, it has been shown that, while some natural and simple problems such as homogeneity, are indeed provably impossible to solve if one only assumes that the data is stationary (or stationary ergodic), many others can be solved using rather simple and intuitive algorithms. The latter problems include clustering and change point estimation. In this volume I summarize these results. The emphasis is on asymptotic consistency, since this the strongest property one can obtain assuming stationarity alone. While for most of the problems for which a solution is found this solution is algorithmically realizable, the main objective in this area of research, the objective which is only partially attained, is to understand what is possible and what is not possible to do for stationary time series. The considered problems include homogeneity testing, clustering with respect to distribution, clustering with respect to independence, change-point estimation, identity testing, and the general question of composite hypotheses testing. For the latter problem, a topological criterion for the existence of a consistent test is presented. In addition, several open questions are discussed.

Finite-time optimality of Bayesian predictors

The problem of sequential probability forecasting is considered in the most general setting: a model set C is given, and it is required to predict as well as possible if any of the measures (environments) in C is chosen to generate the data. No assumptions whatsoever are made on the model class C, in particular, no independence or mixing assumptions; C may not be measurable; there may be no predictor whose loss is sublinear, etc. It is shown that the cumulative loss of any possible predictor can be matched by that of a Bayesian predictor whose prior is discrete and is concentrated on C, up to an additive term of order $\log n$, where $n$ is the time step. The bound holds for every $n$ and every measure in C. This is the first non-asymptotic result of this kind. In addition, a non-matching lower bound is established: it goes to infinity with $n$ but may do so arbitrarily slow.

Hypotheses testing on infinite random graphs

Drawing on some recent results that provide the formalism necessary to definite stationarity for infinite random graphs, this paper initiates the study of statistical and learning questions pertaining to these objects. Specifically, a criterion for the existence of a consistent test for complex hypotheses is presented, generalizing the corresponding results on time series. As an application, it is shown how one can test that a tree has the Markov property, or, more generally, to estimate its memory.

Independence clustering (without a matrix)

The independence clustering problem is considered in the following formulation: given a set $S$ of random variables, it is required to find the finest partitioning $\{U_1,\dots,U_k\}$ of $S$ into clusters such that the clusters $U_1,\dots,U_k$ are mutually independent. Since mutual independence is the target, pairwise similarity measurements are of no use, and thus traditional clustering algorithms are inapplicable. The distribution of the random variables in $S$ is, in general, unknown, but a sample is available. Thus, the problem is cast in terms of time series. Two forms of sampling are considered: i.i.d.\ and stationary time series, with the main emphasis being on the latter, more general, case. A consistent, computationally tractable algorithm for each of the settings is proposed, and a number of open directions for further research are outlined.

Universality of Bayesian mixture predictors

The problem is that of sequential probability forecasting for finite-valued time series. The data is generated by an unknown probability distribution over the space of all one-way infinite sequences. It is known that this measure belongs to a given set C, but the latter is completely arbitrary (uncountably infinite, without any structure given). The performance is measured with asymptotic average log loss. In this work it is shown that the minimax asymptotic performance is always attainable, and it is attained by a convex combination of a countably many measures from the set C (a Bayesian mixture). This was previously only known for the case when the best achievable asymptotic error is 0. This also contrasts previous results that show that in the non-realizable case all Bayesian mixtures may be suboptimal, while there is a predictor that achieves the optimal performance.

Things Bayes can't do

The problem of forecasting conditional probabilities of the next event given the past is considered in a general probabilistic setting. Given an arbitrary (large, uncountable) set C of predictors, we would like to construct a single predictor that performs asymptotically as well as the best predictor in C, on any data. Here we show that there are sets C for which such predictors exist, but none of them is a Bayesian predictor with a prior concentrated on C. In other words, there is a predictor with sublinear regret, but every Bayesian predictor must have a linear regret. This negative finding is in sharp contrast with previous results that establish the opposite for the case when one of the predictors in $C$ achieves asymptotically vanishing error. In such a case, if there is a predictor that achieves asymptotically vanishing error for any measure in C, then there is a Bayesian predictor that also has this property, and whose prior is concentrated on (a countable subset of) C.

Characterizing predictable classes of processes

The problem is sequence prediction in the following setting. A sequence x1,..., xn,... of discrete-valued observations is generated according to some unknown probabilistic law (measure) mu. After observing each outcome, it is required to give the conditional probabilities of the next observation. The measure mu belongs to an arbitrary class C of stochastic processes. We are interested in predictors ? whose conditional probabilities converge to the 'true' mu-conditional probabilities if any mu { C is chosen to generate the data. We show that if such a predictor exists, then a predictor can also be obtained as a convex combination of a countably many elements of C. In other words, it can be obtained as a Bayesian predictor whose prior is concentrated on a countable set. This result is established for two very different measures of performance of prediction, one of which is very strong, namely, total variation, and the other is very weak, namely, prediction in expected average Kullback-Leibler divergence.

Multiple Change Point Estimation in Stationary Ergodic Time Series

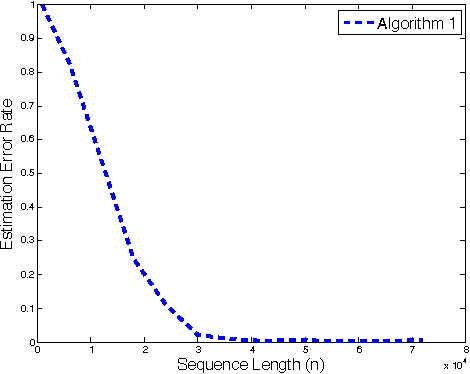
Given a heterogeneous time-series sample, the objective is to find points in time (called change points) where the probability distribution generating the data has changed. The data are assumed to have been generated by arbitrary unknown stationary ergodic distributions. No modelling, independence or mixing assumptions are made. A novel, computationally efficient, nonparametric method is proposed, and is shown to be asymptotically consistent in this general framework. The theoretical results are complemented with experimental evaluations.