Yen-Huan Li
Online Learning Quantum States with the Logarithmic Loss via VB-FTRL
Nov 06, 2023Abstract:Online learning quantum states with the logarithmic loss (LL-OLQS) is a quantum generalization of online portfolio selection, a classic open problem in the field of online learning for over three decades. The problem also emerges in designing randomized optimization algorithms for maximum-likelihood quantum state tomography. Recently, Jezequel et al. (arXiv:2209.13932) proposed the VB-FTRL algorithm, the first nearly regret-optimal algorithm for OPS with moderate computational complexity. In this note, we generalize VB-FTRL for LL-OLQS. Let $d$ denote the dimension and $T$ the number of rounds. The generalized algorithm achieves a regret rate of $O ( d^2 \log ( d + T ) )$ for LL-OLQS. Each iteration of the algorithm consists of solving a semidefinite program that can be implemented in polynomial time by, e.g., cutting-plane methods. For comparison, the best-known regret rate for LL-OLQS is currently $O ( d^2 \log T )$, achieved by the exponential weight method. However, there is no explicit implementation available for the exponential weight method for LL-OLQS. To facilitate the generalization, we introduce the notion of VB-convexity. VB-convexity is a sufficient condition for the logarithmic barrier associated with any function to be convex and is of independent interest.
Fast Minimization of Expected Logarithmic Loss via Stochastic Dual Averaging
Nov 05, 2023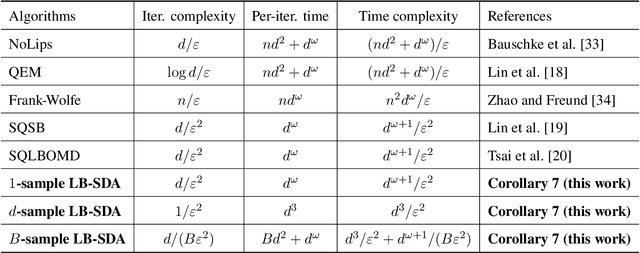
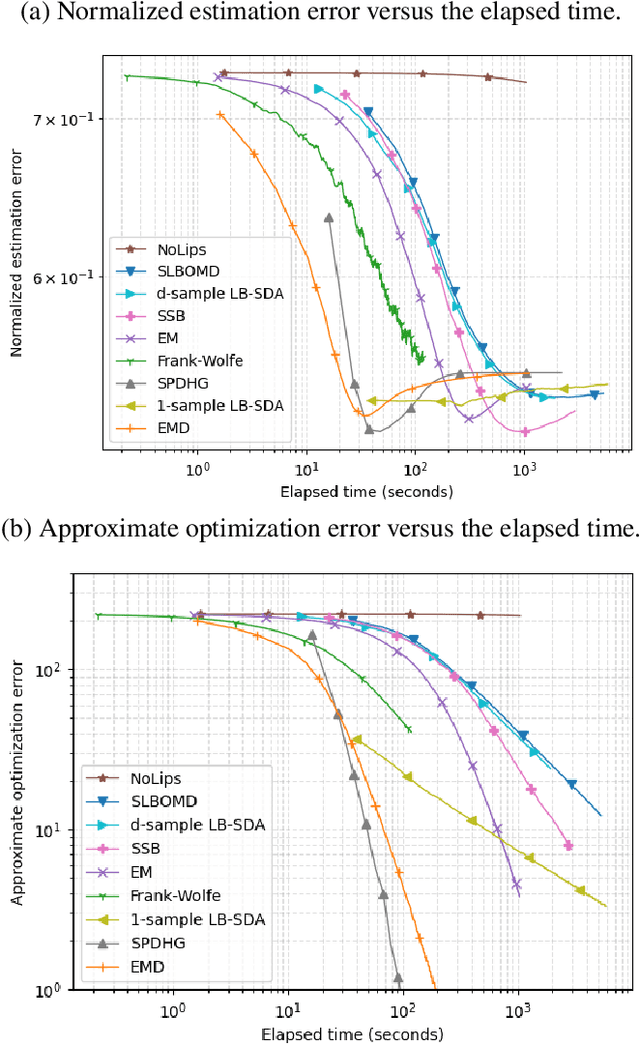
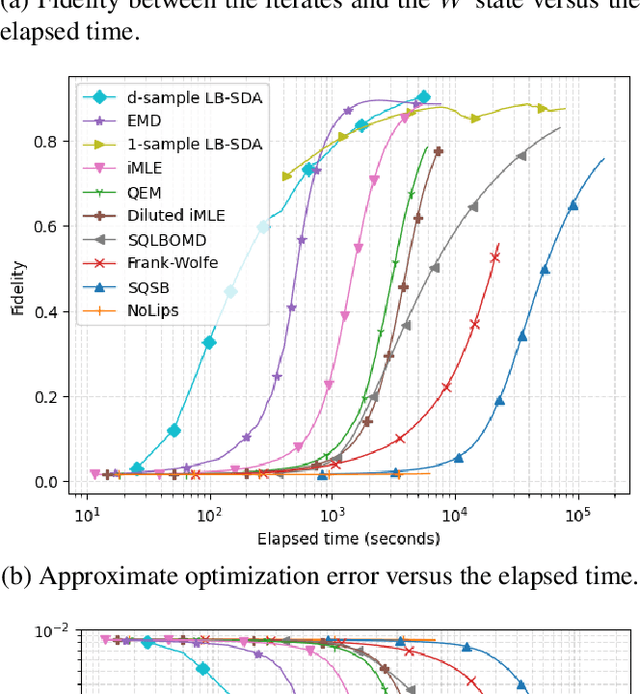
Abstract:Consider the problem of minimizing an expected logarithmic loss over either the probability simplex or the set of quantum density matrices. This problem encompasses tasks such as solving the Poisson inverse problem, computing the maximum-likelihood estimate for quantum state tomography, and approximating positive semi-definite matrix permanents with the currently tightest approximation ratio. Although the optimization problem is convex, standard iteration complexity guarantees for first-order methods do not directly apply due to the absence of Lipschitz continuity and smoothness in the loss function. In this work, we propose a stochastic first-order algorithm named $B$-sample stochastic dual averaging with the logarithmic barrier. For the Poisson inverse problem, our algorithm attains an $\varepsilon$-optimal solution in $\tilde{O} (d^2/\varepsilon^2)$ time, matching the state of the art. When computing the maximum-likelihood estimate for quantum state tomography, our algorithm yields an $\varepsilon$-optimal solution in $\tilde{O} (d^3/\varepsilon^2)$ time, where $d$ denotes the dimension. This improves on the time complexities of existing stochastic first-order methods by a factor of $d^{\omega-2}$ and those of batch methods by a factor of $d^2$, where $\omega$ denotes the matrix multiplication exponent. Numerical experiments demonstrate that empirically, our algorithm outperforms existing methods with explicit complexity guarantees.
Data-Dependent Bounds for Online Portfolio Selection Without Lipschitzness and Smoothness
May 23, 2023Abstract:This work introduces the first small-loss and gradual-variation regret bounds for online portfolio selection, marking the first instances of data-dependent bounds for online convex optimization with non-Lipschitz, non-smooth losses. The algorithms we propose exhibit sublinear regret rates in the worst cases and achieve logarithmic regrets when the data is "easy," with per-iteration time almost linear in the number of investment alternatives. The regret bounds are derived using novel smoothness characterizations of the logarithmic loss, a local norm-based analysis of following the regularized leader (FTRL) with self-concordant regularizers, which are not necessarily barriers, and an implicit variant of optimistic FTRL with the log-barrier.
Faster Stochastic First-Order Method for Maximum-Likelihood Quantum State Tomography
Nov 23, 2022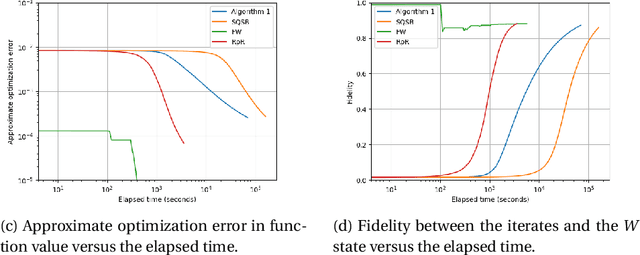
Abstract:In maximum-likelihood quantum state tomography, both the sample size and dimension grow exponentially with the number of qubits. It is therefore desirable to develop a stochastic first-order method, just like stochastic gradient descent for modern machine learning, to compute the maximum-likelihood estimate. To this end, we propose an algorithm called stochastic mirror descent with the Burg entropy. Its expected optimization error vanishes at a $O ( \sqrt{ ( 1 / t ) d \log t } )$ rate, where $d$ and $t$ denote the dimension and number of iterations, respectively. Its per-iteration time complexity is $O ( d^3 )$, independent of the sample size. To the best of our knowledge, this is currently the computationally fastest stochastic first-order method for maximum-likelihood quantum state tomography.
Online Self-Concordant and Relatively Smooth Minimization, With Applications to Online Portfolio Selection and Learning Quantum States
Oct 03, 2022
Abstract:Consider an online convex optimization problem where the loss functions are self-concordant barriers, smooth relative to a convex function $h$, and possibly non-Lipschitz. We analyze the regret of online mirror descent with $h$. Then, based on the result, we prove the following in a unified manner. Denote by $T$ the time horizon and $d$ the parameter dimension. 1. For online portfolio selection, the regret of $\widetilde{\text{EG}}$, a variant of exponentiated gradient due to Helmbold et al., is $\tilde{O} ( T^{2/3} d^{1/3} )$ when $T > 4 d / \log d$. This improves on the original $\tilde{O} ( T^{3/4} d^{1/2} )$ regret bound for $\widetilde{\text{EG}}$. 2. For online portfolio selection, the regret of online mirror descent with the logarithmic barrier is $\tilde{O}(\sqrt{T d})$. The regret bound is the same as that of Soft-Bayes due to Orseau et al. up to logarithmic terms. 3. For online learning quantum states with the logarithmic loss, the regret of online mirror descent with the log-determinant function is also $\tilde{O} ( \sqrt{T d} )$. Its per-iteration time is shorter than all existing algorithms we know.
An Online Algorithm for Maximum-Likelihood Quantum State Tomography
Dec 31, 2020

Abstract:We propose, to the best of our knowledge, the first online algorithm for maximum-likelihood quantum state tomography. Suppose the quantum state to be estimated corresponds to a \( D \)-by-\( D \) density matrix. The per-iteration computational complexity of the algorithm is \( O ( D ^ 3 ) \), independent of the data size. The expected numerical error of the algorithm is $O(\sqrt{ ( 1 / T ) D \log D })$, where $T$ denotes the number of iterations. The algorithm can be viewed as a quantum extension of Soft-Bayes, a recent algorithm for online portfolio selection (Orseau et al. Soft-Bayes: Prod for mixtures of experts with log-loss. \textit{Int. Conf. Algorithmic Learning Theory}. 2017).
Learning-Based Compressive MRI
May 03, 2018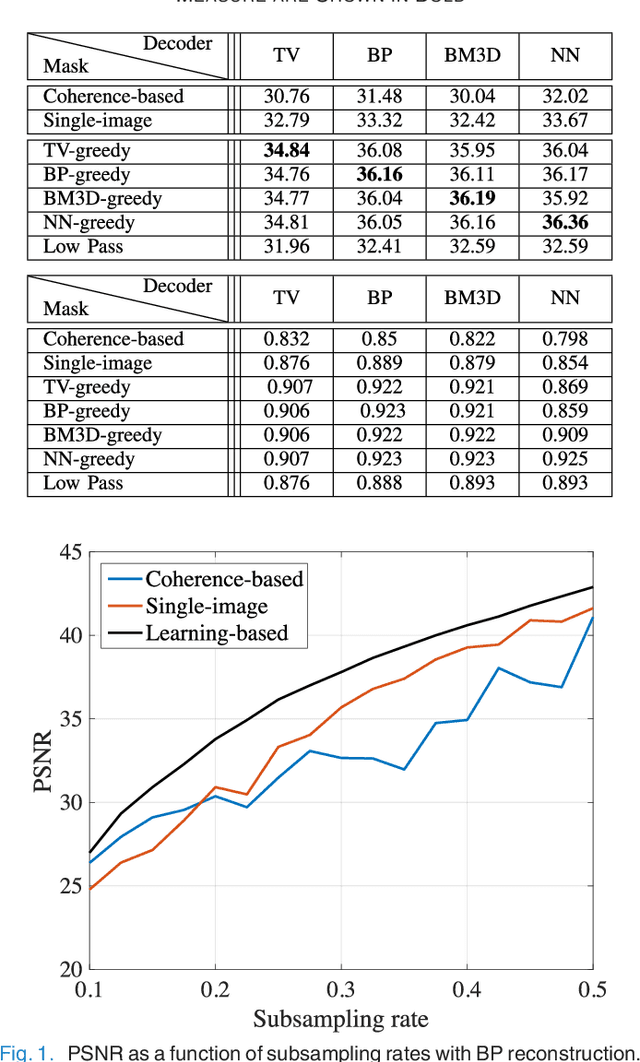

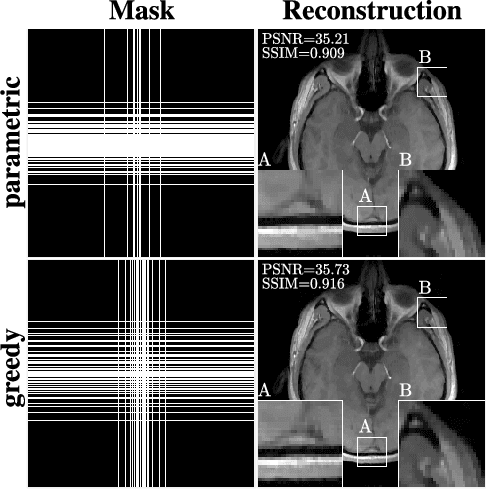
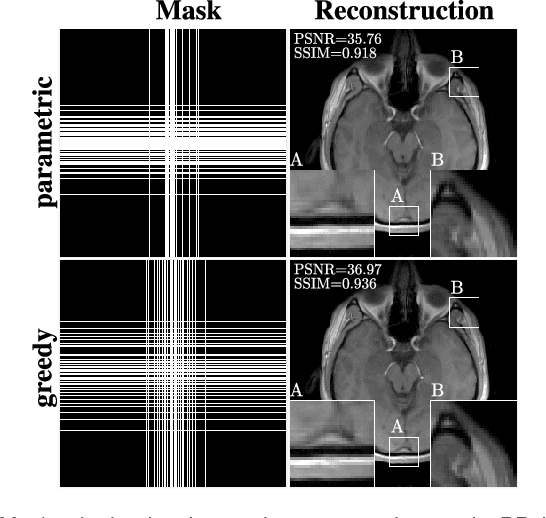
Abstract:In the area of magnetic resonance imaging (MRI), an extensive range of non-linear reconstruction algorithms have been proposed that can be used with general Fourier subsampling patterns. However, the design of these subsampling patterns has typically been considered in isolation from the reconstruction rule and the anatomy under consideration. In this paper, we propose a learning-based framework for optimizing MRI subsampling patterns for a specific reconstruction rule and anatomy, considering both the noiseless and noisy settings. Our learning algorithm has access to a representative set of training signals, and searches for a sampling pattern that performs well on average for the signals in this set. We present a novel parameter-free greedy mask selection method, and show it to be effective for a variety of reconstruction rules and performance metrics. Moreover we also support our numerical findings by providing a rigorous justification of our framework via statistical learning theory.
Composite convex minimization involving self-concordant-like cost functions
Jan 20, 2018



Abstract:The self-concordant-like property of a smooth convex function is a new analytical structure that generalizes the self-concordant notion. While a wide variety of important applications feature the self-concordant-like property, this concept has heretofore remained unexploited in convex optimization. To this end, we develop a variable metric framework of minimizing the sum of a "simple" convex function and a self-concordant-like function. We introduce a new analytic step-size selection procedure and prove that the basic gradient algorithm has improved convergence guarantees as compared to "fast" algorithms that rely on the Lipschitz gradient property. Our numerical tests with real-data sets shows that the practice indeed follows the theory.
Learning-based Compressive Subsampling
Mar 28, 2016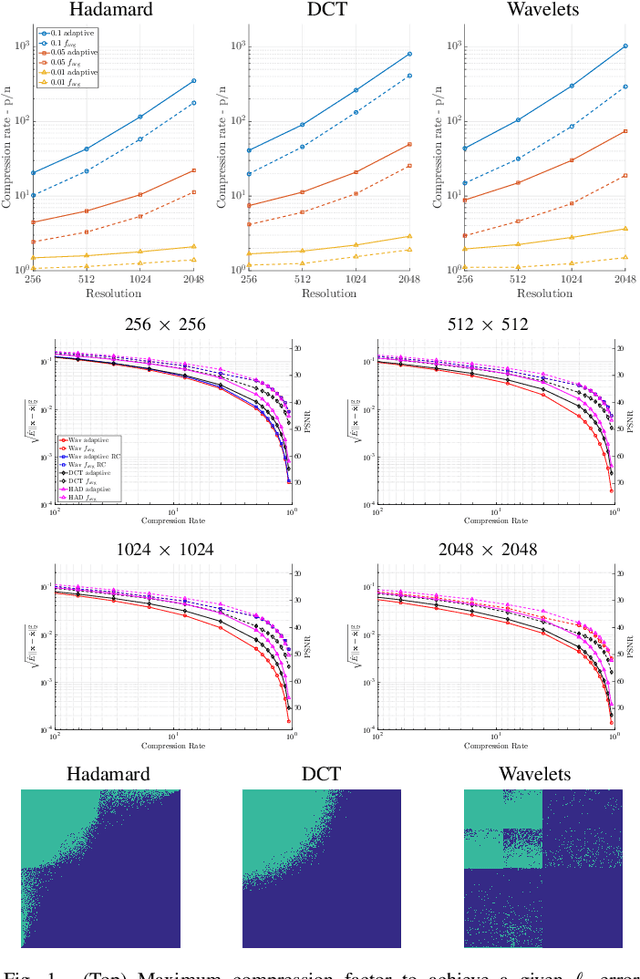
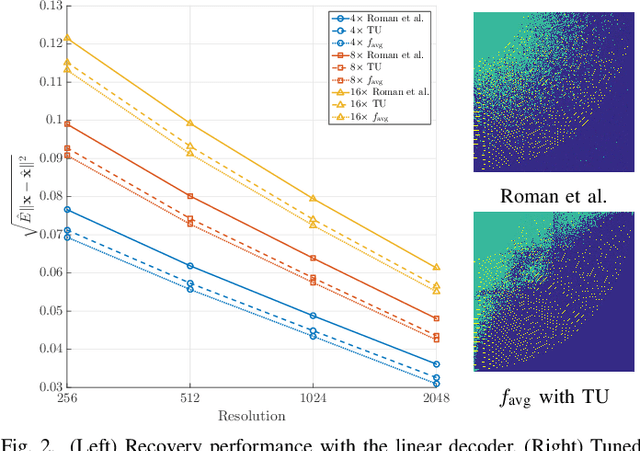
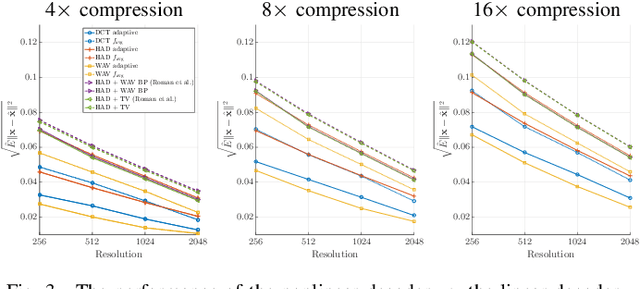
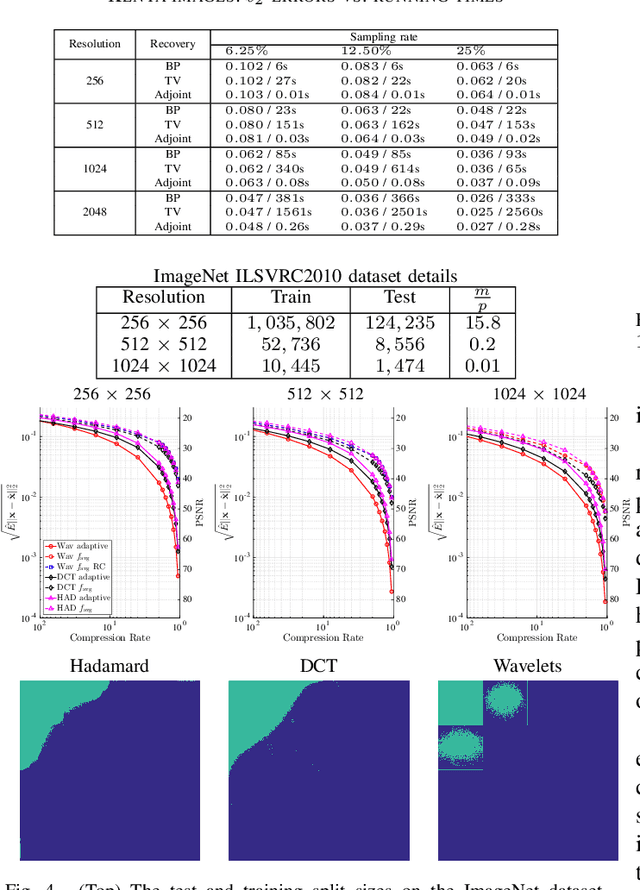
Abstract:The problem of recovering a structured signal $\mathbf{x} \in \mathbb{C}^p$ from a set of dimensionality-reduced linear measurements $\mathbf{b} = \mathbf {A}\mathbf {x}$ arises in a variety of applications, such as medical imaging, spectroscopy, Fourier optics, and computerized tomography. Due to computational and storage complexity or physical constraints imposed by the problem, the measurement matrix $\mathbf{A} \in \mathbb{C}^{n \times p}$ is often of the form $\mathbf{A} = \mathbf{P}_{\Omega}\boldsymbol{\Psi}$ for some orthonormal basis matrix $\boldsymbol{\Psi}\in \mathbb{C}^{p \times p}$ and subsampling operator $\mathbf{P}_{\Omega}: \mathbb{C}^{p} \rightarrow \mathbb{C}^{n}$ that selects the rows indexed by $\Omega$. This raises the fundamental question of how best to choose the index set $\Omega$ in order to optimize the recovery performance. Previous approaches to addressing this question rely on non-uniform \emph{random} subsampling using application-specific knowledge of the structure of $\mathbf{x}$. In this paper, we instead take a principled learning-based approach in which a \emph{fixed} index set is chosen based on a set of training signals $\mathbf{x}_1,\dotsc,\mathbf{x}_m$. We formulate combinatorial optimization problems seeking to maximize the energy captured in these signals in an average-case or worst-case sense, and we show that these can be efficiently solved either exactly or approximately via the identification of modularity and submodularity structures. We provide both deterministic and statistical theoretical guarantees showing how the resulting measurement matrices perform on signals differing from the training signals, and we provide numerical examples showing our approach to be effective on a variety of data sets.
Learning Data Triage: Linear Decoding Works for Compressive MRI
Feb 01, 2016


Abstract:The standard approach to compressive sampling considers recovering an unknown deterministic signal with certain known structure, and designing the sub-sampling pattern and recovery algorithm based on the known structure. This approach requires looking for a good representation that reveals the signal structure, and solving a non-smooth convex minimization problem (e.g., basis pursuit). In this paper, another approach is considered: We learn a good sub-sampling pattern based on available training signals, without knowing the signal structure in advance, and reconstruct an accordingly sub-sampled signal by computationally much cheaper linear reconstruction. We provide a theoretical guarantee on the recovery error, and show via experiments on real-world MRI data the effectiveness of the proposed compressive MRI scheme.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge