Fast Minimization of Expected Logarithmic Loss via Stochastic Dual Averaging

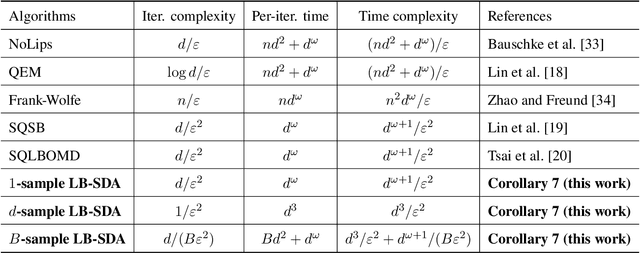
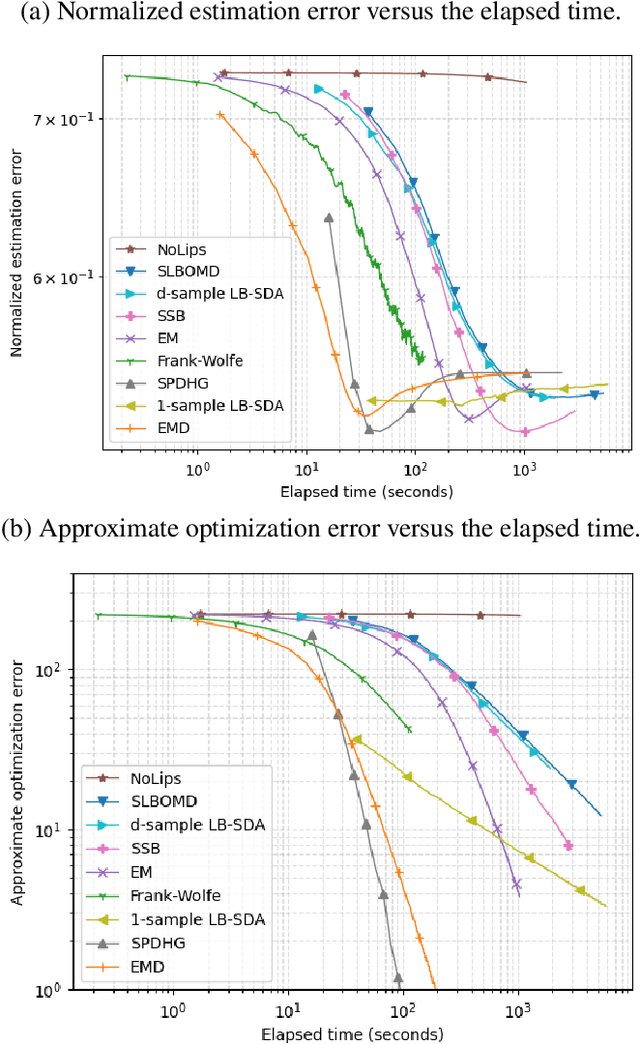
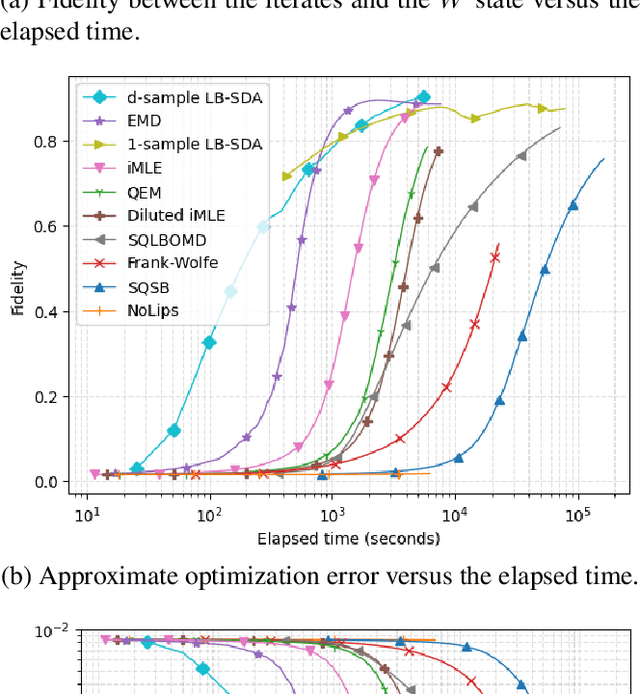
Consider the problem of minimizing an expected logarithmic loss over either the probability simplex or the set of quantum density matrices. This problem encompasses tasks such as solving the Poisson inverse problem, computing the maximum-likelihood estimate for quantum state tomography, and approximating positive semi-definite matrix permanents with the currently tightest approximation ratio. Although the optimization problem is convex, standard iteration complexity guarantees for first-order methods do not directly apply due to the absence of Lipschitz continuity and smoothness in the loss function. In this work, we propose a stochastic first-order algorithm named $B$-sample stochastic dual averaging with the logarithmic barrier. For the Poisson inverse problem, our algorithm attains an $\varepsilon$-optimal solution in $\tilde{O} (d^2/\varepsilon^2)$ time, matching the state of the art. When computing the maximum-likelihood estimate for quantum state tomography, our algorithm yields an $\varepsilon$-optimal solution in $\tilde{O} (d^3/\varepsilon^2)$ time, where $d$ denotes the dimension. This improves on the time complexities of existing stochastic first-order methods by a factor of $d^{\omega-2}$ and those of batch methods by a factor of $d^2$, where $\omega$ denotes the matrix multiplication exponent. Numerical experiments demonstrate that empirically, our algorithm outperforms existing methods with explicit complexity guarantees.