Audio Prompt Adapter: Unleashing Music Editing Abilities for Text-to-Music with Lightweight Finetuning

Text-to-music models allow users to generate nearly realistic musical audio with textual commands. However, editing music audios remains challenging due to the conflicting desiderata of performing fine-grained alterations on the audio while maintaining a simple user interface. To address this challenge, we propose Audio Prompt Adapter (or AP-Adapter), a lightweight addition to pretrained text-to-music models. We utilize AudioMAE to extract features from the input audio, and construct attention-based adapters to feedthese features into the internal layers of AudioLDM2, a diffusion-based text-to-music model. With 22M trainable parameters, AP-Adapter empowers users to harness both global (e.g., genre and timbre) and local (e.g., melody) aspects of music, using the original audio and a short text as inputs. Through objective and subjective studies, we evaluate AP-Adapter on three tasks: timbre transfer, genre transfer, and accompaniment generation. Additionally, we demonstrate its effectiveness on out-of-domain audios containing unseen instruments during training.

MusiConGen: Rhythm and Chord Control for Transformer-Based Text-to-Music Generation

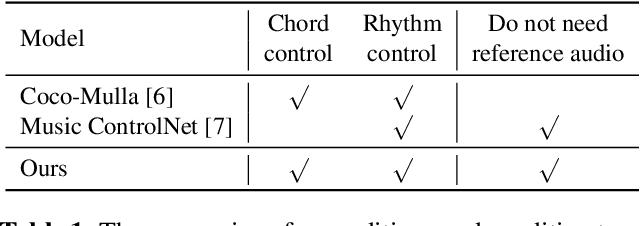
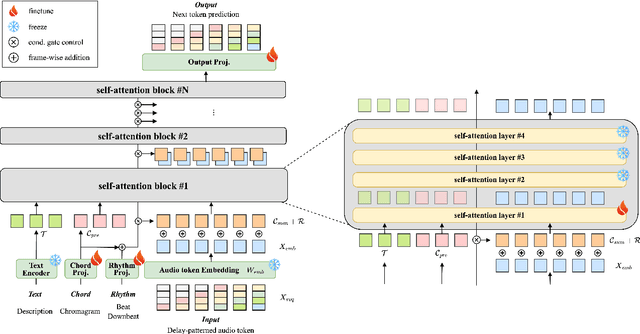
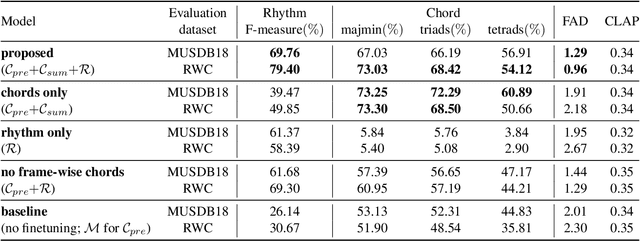
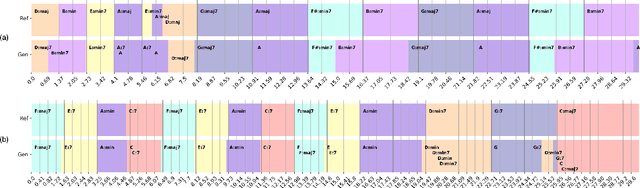
Existing text-to-music models can produce high-quality audio with great diversity. However, textual prompts alone cannot precisely control temporal musical features such as chords and rhythm of the generated music. To address this challenge, we introduce MusiConGen, a temporally-conditioned Transformer-based text-to-music model that builds upon the pretrained MusicGen framework. Our innovation lies in an efficient finetuning mechanism, tailored for consumer-grade GPUs, that integrates automatically-extracted rhythm and chords as the condition signal. During inference, the condition can either be musical features extracted from a reference audio signal, or be user-defined symbolic chord sequence, BPM, and textual prompts. Our performance evaluation on two datasets -- one derived from extracted features and the other from user-created inputs -- demonstrates that MusiConGen can generate realistic backing track music that aligns well with the specified conditions. We open-source the code and model checkpoints, and provide audio examples online, https://musicongen.github.io/musicongen_demo/.

Sample complexity of quantum hypothesis testing

Quantum hypothesis testing has been traditionally studied from the information-theoretic perspective, wherein one is interested in the optimal decay rate of error probabilities as a function of the number of samples of an unknown state. In this paper, we study the sample complexity of quantum hypothesis testing, wherein the goal is to determine the minimum number of samples needed to reach a desired error probability. By making use of the wealth of knowledge that already exists in the literature on quantum hypothesis testing, we characterize the sample complexity of binary quantum hypothesis testing in the symmetric and asymmetric settings, and we provide bounds on the sample complexity of multiple quantum hypothesis testing. In more detail, we prove that the sample complexity of symmetric binary quantum hypothesis testing depends logarithmically on the inverse error probability and inversely on the negative logarithm of the fidelity. As a counterpart of the quantum Stein's lemma, we also find that the sample complexity of asymmetric binary quantum hypothesis testing depends logarithmically on the inverse type~II error probability and inversely on the quantum relative entropy. Finally, we provide lower and upper bounds on the sample complexity of multiple quantum hypothesis testing, with it remaining an intriguing open question to improve these bounds.

Fast Minimization of Expected Logarithmic Loss via Stochastic Dual Averaging

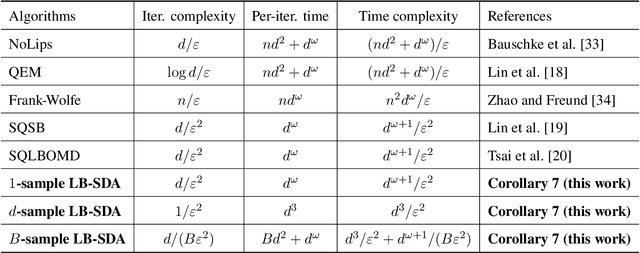
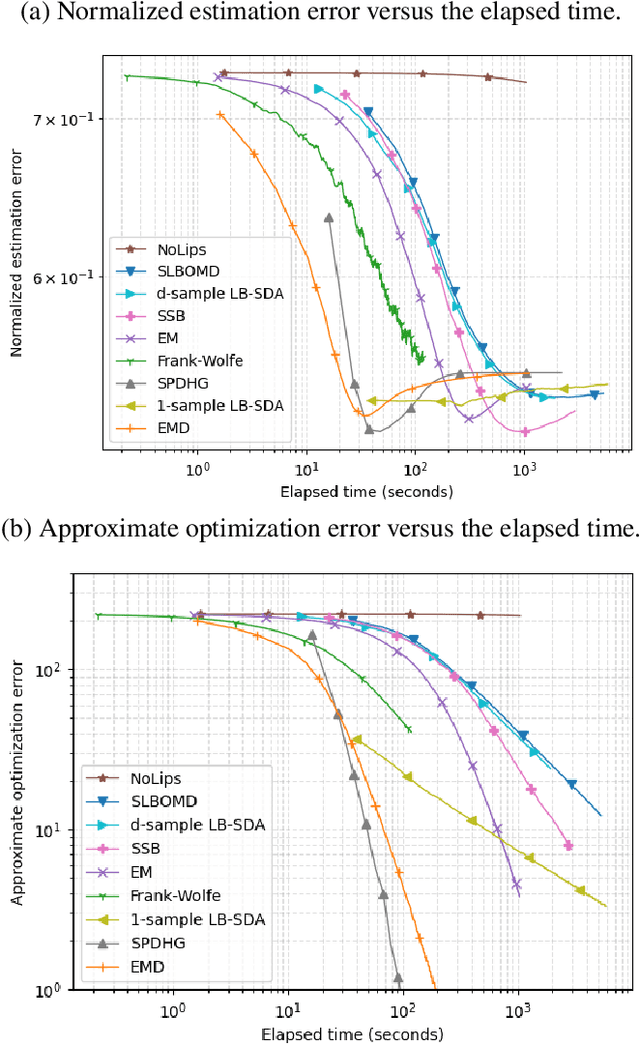
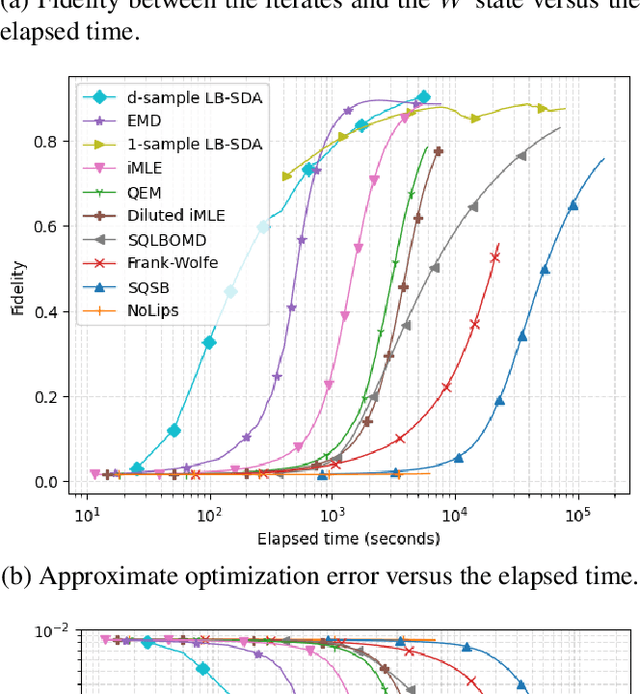
Consider the problem of minimizing an expected logarithmic loss over either the probability simplex or the set of quantum density matrices. This problem encompasses tasks such as solving the Poisson inverse problem, computing the maximum-likelihood estimate for quantum state tomography, and approximating positive semi-definite matrix permanents with the currently tightest approximation ratio. Although the optimization problem is convex, standard iteration complexity guarantees for first-order methods do not directly apply due to the absence of Lipschitz continuity and smoothness in the loss function. In this work, we propose a stochastic first-order algorithm named $B$-sample stochastic dual averaging with the logarithmic barrier. For the Poisson inverse problem, our algorithm attains an $\varepsilon$-optimal solution in $\tilde{O} (d^2/\varepsilon^2)$ time, matching the state of the art. When computing the maximum-likelihood estimate for quantum state tomography, our algorithm yields an $\varepsilon$-optimal solution in $\tilde{O} (d^3/\varepsilon^2)$ time, where $d$ denotes the dimension. This improves on the time complexities of existing stochastic first-order methods by a factor of $d^{\omega-2}$ and those of batch methods by a factor of $d^2$, where $\omega$ denotes the matrix multiplication exponent. Numerical experiments demonstrate that empirically, our algorithm outperforms existing methods with explicit complexity guarantees.

Faster Stochastic First-Order Method for Maximum-Likelihood Quantum State Tomography

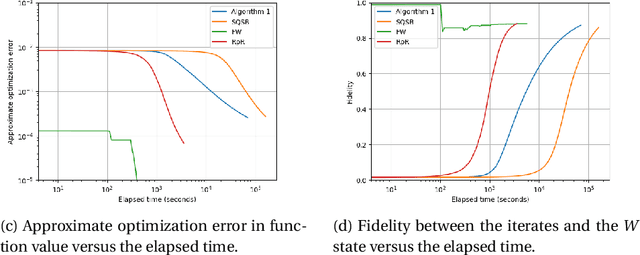
In maximum-likelihood quantum state tomography, both the sample size and dimension grow exponentially with the number of qubits. It is therefore desirable to develop a stochastic first-order method, just like stochastic gradient descent for modern machine learning, to compute the maximum-likelihood estimate. To this end, we propose an algorithm called stochastic mirror descent with the Burg entropy. Its expected optimization error vanishes at a $O ( \sqrt{ ( 1 / t ) d \log t } )$ rate, where $d$ and $t$ denote the dimension and number of iterations, respectively. Its per-iteration time complexity is $O ( d^3 )$, independent of the sample size. To the best of our knowledge, this is currently the computationally fastest stochastic first-order method for maximum-likelihood quantum state tomography.

Online Self-Concordant and Relatively Smooth Minimization, With Applications to Online Portfolio Selection and Learning Quantum States

Consider an online convex optimization problem where the loss functions are self-concordant barriers, smooth relative to a convex function $h$, and possibly non-Lipschitz. We analyze the regret of online mirror descent with $h$. Then, based on the result, we prove the following in a unified manner. Denote by $T$ the time horizon and $d$ the parameter dimension. 1. For online portfolio selection, the regret of $\widetilde{\text{EG}}$, a variant of exponentiated gradient due to Helmbold et al., is $\tilde{O} ( T^{2/3} d^{1/3} )$ when $T > 4 d / \log d$. This improves on the original $\tilde{O} ( T^{3/4} d^{1/2} )$ regret bound for $\widetilde{\text{EG}}$. 2. For online portfolio selection, the regret of online mirror descent with the logarithmic barrier is $\tilde{O}(\sqrt{T d})$. The regret bound is the same as that of Soft-Bayes due to Orseau et al. up to logarithmic terms. 3. For online learning quantum states with the logarithmic loss, the regret of online mirror descent with the log-determinant function is also $\tilde{O} ( \sqrt{T d} )$. Its per-iteration time is shorter than all existing algorithms we know.

The Learnability of Unknown Quantum Measurements

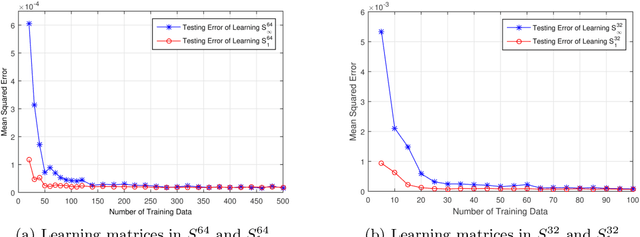
Quantum machine learning has received significant attention in recent years, and promising progress has been made in the development of quantum algorithms to speed up traditional machine learning tasks. In this work, however, we focus on investigating the information-theoretic upper bounds of sample complexity - how many training samples are sufficient to predict the future behaviour of an unknown target function. This kind of problem is, arguably, one of the most fundamental problems in statistical learning theory and the bounds for practical settings can be completely characterised by a simple measure of complexity. Our main result in the paper is that, for learning an unknown quantum measurement, the upper bound, given by the fat-shattering dimension, is linearly proportional to the dimension of the underlying Hilbert space. Learning an unknown quantum state becomes a dual problem to ours, and as a byproduct, we can recover Aaronson's famous result [Proc. R. Soc. A 463:3089-3144 (2007)] solely using a classical machine learning technique. In addition, other famous complexity measures like covering numbers and Rademacher complexities are derived explicitly. We are able to connect measures of sample complexity with various areas in quantum information science, e.g. quantum state/measurement tomography, quantum state discrimination and quantum random access codes, which may be of independent interest. Lastly, with the assistance of general Bloch-sphere representation, we show that learning quantum measurements/states can be mathematically formulated as a neural network. Consequently, classical ML algorithms can be applied to efficiently accomplish the two quantum learning tasks.