Fermi-Dirac thermal measurements: A framework for quantum hypothesis testing and semidefinite optimization

Quantum measurements are the means by which we recover messages encoded into quantum states. They are at the forefront of quantum hypothesis testing, wherein the goal is to perform an optimal measurement for arriving at a correct conclusion. Mathematically, a measurement operator is Hermitian with eigenvalues in [0,1]. By noticing that this constraint on each eigenvalue is the same as that imposed on fermions by the Pauli exclusion principle, we interpret every eigenmode of a measurement operator as an independent effective fermionic mode. Under this perspective, various objective functions in quantum hypothesis testing can be viewed as the total expected energy associated with these fermionic occupation numbers. By instead fixing a temperature and minimizing the total expected fermionic free energy, we find that optimal measurements for these modified objective functions are Fermi-Dirac thermal measurements, wherein their eigenvalues are specified by Fermi-Dirac distributions. In the low-temperature limit, their performance closely approximates that of optimal measurements for quantum hypothesis testing, and we show that their parameters can be learned by classical or hybrid quantum-classical optimization algorithms. This leads to a new quantum machine-learning model, termed Fermi-Dirac machines, consisting of parameterized Fermi-Dirac thermal measurements-an alternative to quantum Boltzmann machines based on thermal states. Beyond hypothesis testing, we show how general semidefinite optimization problems can be solved using this approach, leading to a novel paradigm for semidefinite optimization on quantum computers, in which the goal is to implement thermal measurements rather than prepare thermal states. Finally, we propose quantum algorithms for implementing Fermi-Dirac thermal measurements, and we also propose second-order hybrid quantum-classical optimization algorithms.

Fundamentals of quantum Boltzmann machine learning with visible and hidden units

One of the primary applications of classical Boltzmann machines is generative modeling, wherein the goal is to tune the parameters of a model distribution so that it closely approximates a target distribution. Training relies on estimating the gradient of the relative entropy between the target and model distributions, a task that is well understood when the classical Boltzmann machine has both visible and hidden units. For some years now, it has been an obstacle to generalize this finding to quantum state learning with quantum Boltzmann machines that have both visible and hidden units. In this paper, I derive an analytical expression for the gradient of the quantum relative entropy between a target quantum state and the reduced state of the visible units of a quantum Boltzmann machine. Crucially, this expression is amenable to estimation on a quantum computer, as it involves modular-flow-generated unitary rotations reminiscent of those appearing in my prior work on rotated Petz recovery maps. This leads to a quantum algorithm for gradient estimation in this setting. I then specialize the setting to quantum visible units and classical hidden units, and vice versa, and provide analytical expressions for the gradients, along with quantum algorithms for estimating them. Finally, I replace the quantum relative entropy objective function with the Petz-Tsallis relative entropy; here I develop an analytical expression for the gradient and sketch a quantum algorithm for estimating it, as an application of a novel formula for the derivative of the matrix power function, which also involves modular-flow-generated unitary rotations. Ultimately, this paper demarcates progress in training quantum Boltzmann machines with visible and hidden units for generative modeling and quantum state learning.

Quantum Fisher information matrices from Rényi relative entropies

Quantum generalizations of the Fisher information are important in quantum information science, with applications in high energy and condensed matter physics and in quantum estimation theory, machine learning, and optimization. One can derive a quantum generalization of the Fisher information matrix in a natural way as the Hessian matrix arising in a Taylor expansion of a smooth divergence. Such an approach is appealing for quantum information theorists, given the ubiquity of divergences in quantum information theory. In contrast to the classical case, there is not a unique quantum generalization of the Fisher information matrix, similar to how there is not a unique quantum generalization of the relative entropy or the R\'enyi relative entropy. In this paper, I derive information matrices arising from the log-Euclidean, $\alpha$-$z$, and geometric R\'enyi relative entropies, with the main technical tool for doing so being the method of divided differences for calculating matrix derivatives. Interestingly, for all non-negative values of the R\'enyi parameter $\alpha$, the log-Euclidean R\'enyi relative entropy leads to the Kubo-Mori information matrix, and the geometric R\'enyi relative entropy leads to the right-logarithmic derivative Fisher information matrix. Thus, the resulting information matrices obey the data-processing inequality for all non-negative values of the R\'enyi parameter $\alpha$ even though the original quantities do not. Additionally, I derive and establish basic properties of $\alpha$-$z$ information matrices resulting from the $\alpha$-$z$ R\'enyi relative entropies. For parameterized thermal states, I establish formulas for their $\alpha$-$z$ information matrices and hybrid quantum-classical algorithms for estimating them, with applications in quantum Boltzmann machine learning.

Constrained free energy minimization for the design of thermal states and stabilizer thermodynamic systems

A quantum thermodynamic system is described by a Hamiltonian and a list of conserved, non-commuting charges, and a fundamental goal is to determine the minimum energy of the system subject to constraints on the charges. Recently, [Liu et al., arXiv:2505.04514] proposed first- and second-order classical and hybrid quantum-classical algorithms for solving a dual chemical potential maximization problem, and they proved that these algorithms converge to global optima by means of gradient-ascent approaches. In this paper, we benchmark these algorithms on several problems of interest in thermodynamics, including one- and two-dimensional quantum Heisenberg models with nearest and next-to-nearest neighbor interactions and with the charges set to the total $x$, $y$, and $z$ magnetizations. We also offer an alternative compelling interpretation of these algorithms as methods for designing ground and thermal states of controllable Hamiltonians, with potential applications in molecular and material design. Furthermore, we introduce stabilizer thermodynamic systems as thermodynamic systems based on stabilizer codes, with the Hamiltonian constructed from a given code's stabilizer operators and the charges constructed from the code's logical operators. We benchmark the aforementioned algorithms on several examples of stabilizer thermodynamic systems, including those constructed from the one-to-three-qubit repetition code, the perfect one-to-five-qubit code, and the two-to-four-qubit error-detecting code. Finally, we observe that the aforementioned hybrid quantum-classical algorithms, when applied to stabilizer thermodynamic systems, can serve as alternative methods for encoding qubits into stabilizer codes at a fixed temperature, and we provide an effective method for warm-starting these encoding algorithms whenever a single qubit is encoded into multiple physical qubits.

Quantum thermodynamics and semi-definite optimization

In quantum thermodynamics, a system is described by a Hamiltonian and a list of non-commuting charges representing conserved quantities like particle number or electric charge, and an important goal is to determine the system's minimum energy in the presence of these conserved charges. In optimization theory, a semi-definite program (SDP) involves a linear objective function optimized over the cone of positive semi-definite operators intersected with an affine space. These problems arise from differing motivations in the physics and optimization communities and are phrased using very different terminology, yet they are essentially identical mathematically. By adopting Jaynes' mindset motivated by quantum thermodynamics, we observe that minimizing free energy in the aforementioned thermodynamics problem, instead of energy, leads to an elegant solution in terms of a dual chemical potential maximization problem that is concave in the chemical potential parameters. As such, one can employ standard (stochastic) gradient ascent methods to find the optimal values of these parameters, and these methods are guaranteed to converge quickly. At low temperature, the minimum free energy provides an excellent approximation for the minimum energy. We then show how this Jaynes-inspired gradient-ascent approach can be used in both first- and second-order classical and hybrid quantum-classical algorithms for minimizing energy, and equivalently, how it can be used for solving SDPs, with guarantees on the runtimes of the algorithms. The approach discussed here is well grounded in quantum thermodynamics and, as such, provides physical motivation underpinning why algorithms published fifty years after Jaynes' seminal work, including the matrix multiplicative weights update method, the matrix exponentiated gradient update method, and their quantum algorithmic generalizations, perform well at solving SDPs.

Query Complexity of Classical and Quantum Channel Discrimination

Quantum channel discrimination has been studied from an information-theoretic perspective, wherein one is interested in the optimal decay rate of error probabilities as a function of the number of unknown channel accesses. In this paper, we study the query complexity of quantum channel discrimination, wherein the goal is to determine the minimum number of channel uses needed to reach a desired error probability. To this end, we show that the query complexity of binary channel discrimination depends logarithmically on the inverse error probability and inversely on the negative logarithm of the (geometric and Holevo) channel fidelity. As a special case of these findings, we precisely characterize the query complexity of discriminating between two classical channels. We also provide lower and upper bounds on the query complexity of binary asymmetric channel discrimination and multiple quantum channel discrimination. For the former, the query complexity depends on the geometric R\'enyi and Petz R\'enyi channel divergences, while for the latter, it depends on the negative logarithm of (geometric and Uhlmann) channel fidelity. For multiple channel discrimination, the upper bound scales as the logarithm of the number of channels.

Quantum Doeblin Coefficients: Interpretations and Applications

In classical information theory, the Doeblin coefficient of a classical channel provides an efficiently computable upper bound on the total-variation contraction coefficient of the channel, leading to what is known as a strong data-processing inequality. Here, we investigate quantum Doeblin coefficients as a generalization of the classical concept. In particular, we define various new quantum Doeblin coefficients, one of which has several desirable properties, including concatenation and multiplicativity, in addition to being efficiently computable. We also develop various interpretations of two of the quantum Doeblin coefficients, including representations as minimal singlet fractions, exclusion values, reverse max-mutual and oveloH informations, reverse robustnesses, and hypothesis testing reverse mutual and oveloH informations. Our interpretations of quantum Doeblin coefficients as either entanglement-assisted or unassisted exclusion values are particularly appealing, indicating that they are proportional to the best possible error probabilities one could achieve in state-exclusion tasks by making use of the channel. We also outline various applications of quantum Doeblin coefficients, ranging from limitations on quantum machine learning algorithms that use parameterized quantum circuits (noise-induced barren plateaus), on error mitigation protocols, on the sample complexity of noisy quantum hypothesis testing, on the fairness of noisy quantum models, and on mixing times of time-varying channels. All of these applications make use of the fact that quantum Doeblin coefficients appear in upper bounds on various trace-distance contraction coefficients of a channel. Furthermore, in all of these applications, our analysis using Doeblin coefficients provides improvements of various kinds over contributions from prior literature, both in terms of generality and being efficiently computable.

Measured Hockey-Stick Divergence and its Applications to Quantum Pufferfish Privacy

The hockey-stick divergence is a fundamental quantity characterizing several statistical privacy frameworks that ensure privacy for classical and quantum data. In such quantum privacy frameworks, the adversary is allowed to perform all possible measurements. However, in practice, there are typically limitations to the set of measurements that can be performed. To this end, here, we comprehensively analyze the measured hockey-stick divergence under several classes of practically relevant measurement classes. We prove several of its properties, including data processing and convexity. We show that it is efficiently computable by semi-definite programming for some classes of measurements and can be analytically evaluated for Werner and isotropic states. Notably, we show that the measured hockey-stick divergence characterizes optimal privacy parameters in the quantum pufferfish privacy framework. With this connection and the developed technical tools, we enable methods to quantify and audit privacy for several practically relevant settings. Lastly, we introduce the measured hockey-stick divergence of channels and explore its applications in ensuring privacy for channels.

Natural gradient and parameter estimation for quantum Boltzmann machines

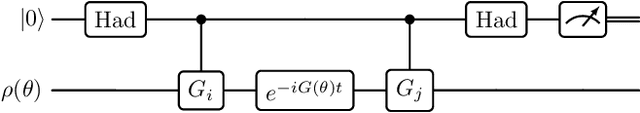
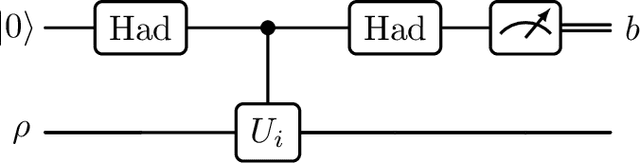
Thermal states play a fundamental role in various areas of physics, and they are becoming increasingly important in quantum information science, with applications related to semi-definite programming, quantum Boltzmann machine learning, Hamiltonian learning, and the related task of estimating the parameters of a Hamiltonian. Here we establish formulas underlying the basic geometry of parameterized thermal states, and we delineate quantum algorithms for estimating the values of these formulas. More specifically, we prove formulas for the Fisher--Bures and Kubo--Mori information matrices of parameterized thermal states, and our quantum algorithms for estimating their matrix elements involve a combination of classical sampling, Hamiltonian simulation, and the Hadamard test. These results have applications in developing a natural gradient descent algorithm for quantum Boltzmann machine learning, which takes into account the geometry of thermal states, and in establishing fundamental limitations on the ability to estimate the parameters of a Hamiltonian, when given access to thermal-state samples. For the latter task, and for the special case of estimating a single parameter, we sketch an algorithm that realizes a measurement that is asymptotically optimal for the estimation task. We finally stress that the natural gradient descent algorithm developed here can be used for any machine learning problem that employs the quantum Boltzmann machine ansatz.

Quantum Boltzmann machine learning of ground-state energies

Estimating the ground-state energy of Hamiltonians is a fundamental task for which it is believed that quantum computers can be helpful. Several approaches have been proposed toward this goal, including algorithms based on quantum phase estimation and hybrid quantum-classical optimizers involving parameterized quantum circuits, the latter falling under the umbrella of the variational quantum eigensolver. Here, we analyze the performance of quantum Boltzmann machines for this task, which is a less explored ansatz based on parameterized thermal states and which is not known to suffer from the barren-plateau problem. We delineate a hybrid quantum-classical algorithm for this task and rigorously prove that it converges to an $\varepsilon$-approximate stationary point of the energy function optimized over parameter space, while using a number of parameterized-thermal-state samples that is polynomial in $\varepsilon^{-1}$, the number of parameters, and the norm of the Hamiltonian being optimized. Our algorithm estimates the gradient of the energy function efficiently by means of a novel quantum circuit construction that combines classical sampling, Hamiltonian simulation, and the Hadamard test, thus overcoming a key obstacle to quantum Boltzmann machine learning that has been left open since [Amin \textit{et al.}, Phys.~Rev.~X \textbf{8}, 021050 (2018)]. Additionally supporting our main claims are calculations of the gradient and Hessian of the energy function, as well as an upper bound on the matrix elements of the latter that is used in the convergence analysis.