Sreejith Sreekumar
Quantum Neural Estimation of Entropies
Jul 03, 2023
Abstract:Entropy measures quantify the amount of information and correlations present in a quantum system. In practice, when the quantum state is unknown and only copies thereof are available, one must resort to the estimation of such entropy measures. Here we propose a variational quantum algorithm for estimating the von Neumann and R\'enyi entropies, as well as the measured relative entropy and measured R\'enyi relative entropy. Our approach first parameterizes a variational formula for the measure of interest by a quantum circuit and a classical neural network, and then optimizes the resulting objective over parameter space. Numerical simulations of our quantum algorithm are provided, using a noiseless quantum simulator. The algorithm provides accurate estimates of the various entropy measures for the examples tested, which renders it as a promising approach for usage in downstream tasks.
Neural Estimation of Statistical Divergences
Oct 07, 2021Abstract:Statistical divergences (SDs), which quantify the dissimilarity between probability distributions, are a basic constituent of statistical inference and machine learning. A modern method for estimating those divergences relies on parametrizing an empirical variational form by a neural network (NN) and optimizing over parameter space. Such neural estimators are abundantly used in practice, but corresponding performance guarantees are partial and call for further exploration. In particular, there is a fundamental tradeoff between the two sources of error involved: approximation and empirical estimation. While the former needs the NN class to be rich and expressive, the latter relies on controlling complexity. We explore this tradeoff for an estimator based on a shallow NN by means of non-asymptotic error bounds, focusing on four popular $\mathsf{f}$-divergences -- Kullback-Leibler, chi-squared, squared Hellinger, and total variation. Our analysis relies on non-asymptotic function approximation theorems and tools from empirical process theory. The bounds reveal the tension between the NN size and the number of samples, and enable to characterize scaling rates thereof that ensure consistency. For compactly supported distributions, we further show that neural estimators with a slightly different NN growth-rate are near minimax rate-optimal, achieving the parametric convergence rate up to logarithmic factors.
Non-Asymptotic Performance Guarantees for Neural Estimation of $\mathsf{f}$-Divergences
Mar 16, 2021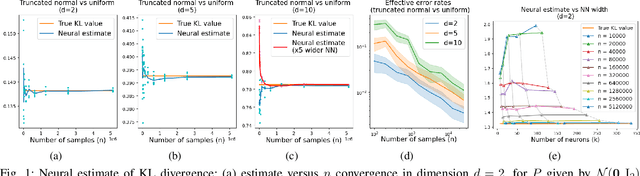
Abstract:Statistical distances (SDs), which quantify the dissimilarity between probability distributions, are central to machine learning and statistics. A modern method for estimating such distances from data relies on parametrizing a variational form by a neural network (NN) and optimizing it. These estimators are abundantly used in practice, but corresponding performance guarantees are partial and call for further exploration. In particular, there seems to be a fundamental tradeoff between the two sources of error involved: approximation and estimation. While the former needs the NN class to be rich and expressive, the latter relies on controlling complexity. This paper explores this tradeoff by means of non-asymptotic error bounds, focusing on three popular choices of SDs -- Kullback-Leibler divergence, chi-squared divergence, and squared Hellinger distance. Our analysis relies on non-asymptotic function approximation theorems and tools from empirical process theory. Numerical results validating the theory are also provided.
Communicate to Learn at the Edge
Sep 28, 2020
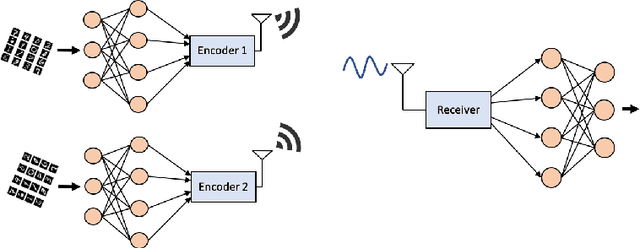
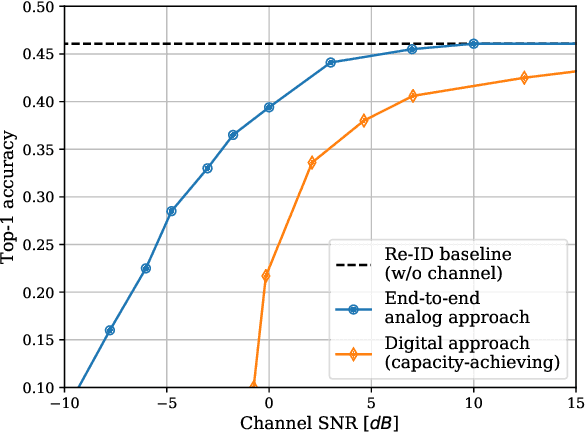
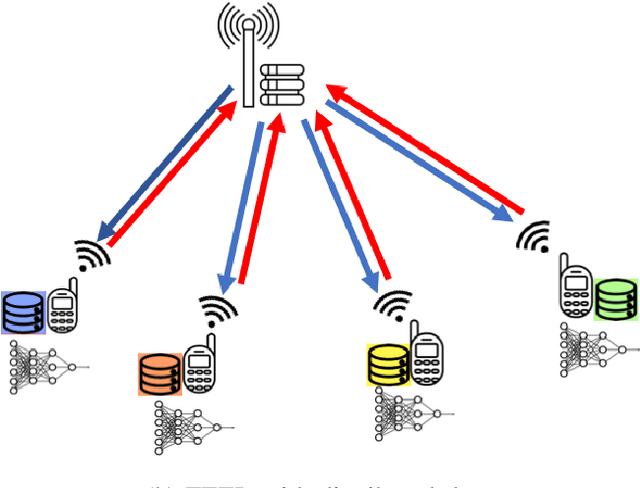
Abstract:Bringing the success of modern machine learning (ML) techniques to mobile devices can enable many new services and businesses, but also poses significant technical and research challenges. Two factors that are critical for the success of ML algorithms are massive amounts of data and processing power, both of which are plentiful, yet highly distributed at the network edge. Moreover, edge devices are connected through bandwidth- and power-limited wireless links that suffer from noise, time-variations, and interference. Information and coding theory have laid the foundations of reliable and efficient communications in the presence of channel imperfections, whose application in modern wireless networks have been a tremendous success. However, there is a clear disconnect between the current coding and communication schemes, and the ML algorithms deployed at the network edge. In this paper, we challenge the current approach that treats these problems separately, and argue for a joint communication and learning paradigm for both the training and inference stages of edge learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge