Natural gradient and parameter estimation for quantum Boltzmann machines

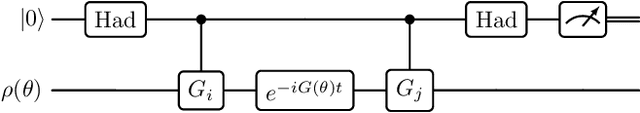
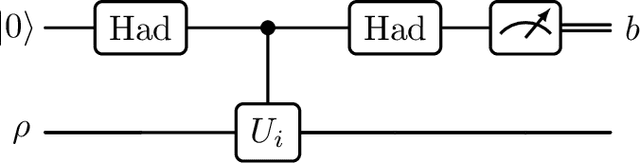
Thermal states play a fundamental role in various areas of physics, and they are becoming increasingly important in quantum information science, with applications related to semi-definite programming, quantum Boltzmann machine learning, Hamiltonian learning, and the related task of estimating the parameters of a Hamiltonian. Here we establish formulas underlying the basic geometry of parameterized thermal states, and we delineate quantum algorithms for estimating the values of these formulas. More specifically, we prove formulas for the Fisher--Bures and Kubo--Mori information matrices of parameterized thermal states, and our quantum algorithms for estimating their matrix elements involve a combination of classical sampling, Hamiltonian simulation, and the Hadamard test. These results have applications in developing a natural gradient descent algorithm for quantum Boltzmann machine learning, which takes into account the geometry of thermal states, and in establishing fundamental limitations on the ability to estimate the parameters of a Hamiltonian, when given access to thermal-state samples. For the latter task, and for the special case of estimating a single parameter, we sketch an algorithm that realizes a measurement that is asymptotically optimal for the estimation task. We finally stress that the natural gradient descent algorithm developed here can be used for any machine learning problem that employs the quantum Boltzmann machine ansatz.

Quantum Boltzmann machine learning of ground-state energies

Estimating the ground-state energy of Hamiltonians is a fundamental task for which it is believed that quantum computers can be helpful. Several approaches have been proposed toward this goal, including algorithms based on quantum phase estimation and hybrid quantum-classical optimizers involving parameterized quantum circuits, the latter falling under the umbrella of the variational quantum eigensolver. Here, we analyze the performance of quantum Boltzmann machines for this task, which is a less explored ansatz based on parameterized thermal states and which is not known to suffer from the barren-plateau problem. We delineate a hybrid quantum-classical algorithm for this task and rigorously prove that it converges to an $\varepsilon$-approximate stationary point of the energy function optimized over parameter space, while using a number of parameterized-thermal-state samples that is polynomial in $\varepsilon^{-1}$, the number of parameters, and the norm of the Hamiltonian being optimized. Our algorithm estimates the gradient of the energy function efficiently by means of a novel quantum circuit construction that combines classical sampling, Hamiltonian simulation, and the Hadamard test, thus overcoming a key obstacle to quantum Boltzmann machine learning that has been left open since [Amin \textit{et al.}, Phys.~Rev.~X \textbf{8}, 021050 (2018)]. Additionally supporting our main claims are calculations of the gradient and Hessian of the energy function, as well as an upper bound on the matrix elements of the latter that is used in the convergence analysis.

Quantum Neural Estimation of Entropies

Entropy measures quantify the amount of information and correlations present in a quantum system. In practice, when the quantum state is unknown and only copies thereof are available, one must resort to the estimation of such entropy measures. Here we propose a variational quantum algorithm for estimating the von Neumann and R\'enyi entropies, as well as the measured relative entropy and measured R\'enyi relative entropy. Our approach first parameterizes a variational formula for the measure of interest by a quantum circuit and a classical neural network, and then optimizes the resulting objective over parameter space. Numerical simulations of our quantum algorithm are provided, using a noiseless quantum simulator. The algorithm provides accurate estimates of the various entropy measures for the examples tested, which renders it as a promising approach for usage in downstream tasks.

Multi-class Brain Tumor Segmentation using Graph Attention Network

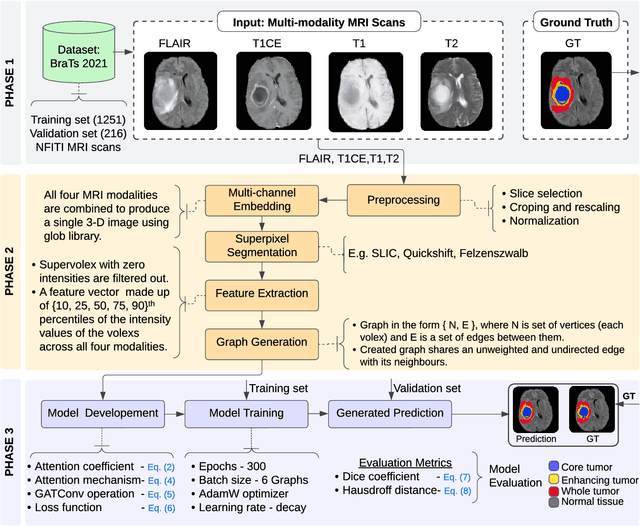
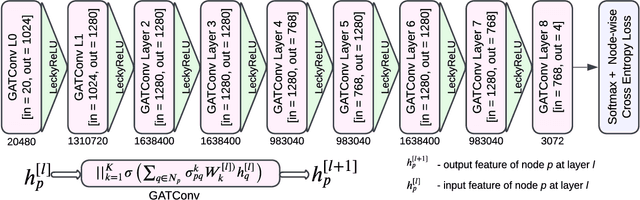
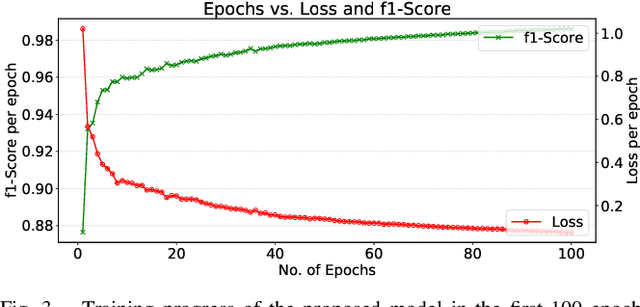
Brain tumor segmentation from magnetic resonance imaging (MRI) plays an important role in diagnostic radiology. To overcome the practical issues in manual approaches, there is a huge demand for building automatic tumor segmentation algorithms. This work introduces an efficient brain tumor summation model by exploiting the advancement in MRI and graph neural networks (GNNs). The model represents the volumetric MRI as a region adjacency graph (RAG) and learns to identify the type of tumors through a graph attention network (GAT) -- a variant of GNNs. The ablation analysis conducted on two benchmark datasets proves that the proposed model can produce competitive results compared to the leading-edge solutions. It achieves mean dice scores of 0.91, 0.86, 0.79, and mean Hausdorff distances in the 95th percentile (HD95) of 5.91, 6.08, and 9.52 mm, respectively, for whole tumor, core tumor, and enhancing tumor segmentation on BraTS2021 validation dataset. On average, these performances are >6\% and >50%, compared to a GNN-based baseline model, respectively, on dice score and HD95 evaluation metrics.