Fermi-Dirac thermal measurements: A framework for quantum hypothesis testing and semidefinite optimization

Quantum measurements are the means by which we recover messages encoded into quantum states. They are at the forefront of quantum hypothesis testing, wherein the goal is to perform an optimal measurement for arriving at a correct conclusion. Mathematically, a measurement operator is Hermitian with eigenvalues in [0,1]. By noticing that this constraint on each eigenvalue is the same as that imposed on fermions by the Pauli exclusion principle, we interpret every eigenmode of a measurement operator as an independent effective fermionic mode. Under this perspective, various objective functions in quantum hypothesis testing can be viewed as the total expected energy associated with these fermionic occupation numbers. By instead fixing a temperature and minimizing the total expected fermionic free energy, we find that optimal measurements for these modified objective functions are Fermi-Dirac thermal measurements, wherein their eigenvalues are specified by Fermi-Dirac distributions. In the low-temperature limit, their performance closely approximates that of optimal measurements for quantum hypothesis testing, and we show that their parameters can be learned by classical or hybrid quantum-classical optimization algorithms. This leads to a new quantum machine-learning model, termed Fermi-Dirac machines, consisting of parameterized Fermi-Dirac thermal measurements-an alternative to quantum Boltzmann machines based on thermal states. Beyond hypothesis testing, we show how general semidefinite optimization problems can be solved using this approach, leading to a novel paradigm for semidefinite optimization on quantum computers, in which the goal is to implement thermal measurements rather than prepare thermal states. Finally, we propose quantum algorithms for implementing Fermi-Dirac thermal measurements, and we also propose second-order hybrid quantum-classical optimization algorithms.

Beyond Benchmarks of IUGC: Rethinking Requirements of Deep Learning Methods for Intrapartum Ultrasound Biometry from Fetal Ultrasound Videos

A substantial proportion (45\%) of maternal deaths, neonatal deaths, and stillbirths occur during the intrapartum phase, with a particularly high burden in low- and middle-income countries. Intrapartum biometry plays a critical role in monitoring labor progression; however, the routine use of ultrasound in resource-limited settings is hindered by a shortage of trained sonographers. To address this challenge, the Intrapartum Ultrasound Grand Challenge (IUGC), co-hosted with MICCAI 2024, was launched. The IUGC introduces a clinically oriented multi-task automatic measurement framework that integrates standard plane classification, fetal head-pubic symphysis segmentation, and biometry, enabling algorithms to exploit complementary task information for more accurate estimation. Furthermore, the challenge releases the largest multi-center intrapartum ultrasound video dataset to date, comprising 774 videos (68,106 frames) collected from three hospitals, providing a robust foundation for model training and evaluation. In this study, we present a comprehensive overview of the challenge design, review the submissions from eight participating teams, and analyze their methods from five perspectives: preprocessing, data augmentation, learning strategy, model architecture, and post-processing. In addition, we perform a systematic analysis of the benchmark results to identify key bottlenecks, explore potential solutions, and highlight open challenges for future research. Although encouraging performance has been achieved, our findings indicate that the field remains at an early stage, and further in-depth investigation is required before large-scale clinical deployment. All benchmark solutions and the complete dataset have been publicly released to facilitate reproducible research and promote continued advances in automatic intrapartum ultrasound biometry.

Improved Offline Reinforcement Learning via Quantum Metric Encoding

Reinforcement learning (RL) with limited samples is common in real-world applications. However, offline RL performance under this constraint is often suboptimal. We consider an alternative approach to dealing with limited samples by introducing the Quantum Metric Encoder (QME). In this methodology, instead of applying the RL framework directly on the original states and rewards, we embed the states into a more compact and meaningful representation, where the structure of the encoding is inspired by quantum circuits. For classical data, QME is a classically simulable, trainable unitary embedding and thus serves as a quantum-inspired module, on a classical device. For quantum data in the form of quantum states, QME can be implemented directly on quantum hardware, allowing for training without measurement or re-encoding. We evaluated QME on three datasets, each limited to 100 samples. We use Soft-Actor-Critic (SAC) and Implicit-Q-Learning (IQL), two well-known RL algorithms, to demonstrate the effectiveness of our approach. From the experimental results, we find that training offline RL agents on QME-embedded states with decoded rewards yields significantly better performance than training on the original states and rewards. On average across the three datasets, for maximum reward performance, we achieve a 116.2% improvement for SAC and 117.6% for IQL. We further investigate the $Δ$-hyperbolicity of our framework, a geometric property of the state space known to be important for the RL training efficacy. The QME-embedded states exhibit low $Δ$-hyperbolicity, suggesting that the improvement after embedding arises from the modified geometry of the state space induced by QME. Thus, the low $Δ$-hyperbolicity and the corresponding effectiveness of QME could provide valuable information for developing efficient offline RL methods under limited-sample conditions.

Constrained free energy minimization for the design of thermal states and stabilizer thermodynamic systems

A quantum thermodynamic system is described by a Hamiltonian and a list of conserved, non-commuting charges, and a fundamental goal is to determine the minimum energy of the system subject to constraints on the charges. Recently, [Liu et al., arXiv:2505.04514] proposed first- and second-order classical and hybrid quantum-classical algorithms for solving a dual chemical potential maximization problem, and they proved that these algorithms converge to global optima by means of gradient-ascent approaches. In this paper, we benchmark these algorithms on several problems of interest in thermodynamics, including one- and two-dimensional quantum Heisenberg models with nearest and next-to-nearest neighbor interactions and with the charges set to the total $x$, $y$, and $z$ magnetizations. We also offer an alternative compelling interpretation of these algorithms as methods for designing ground and thermal states of controllable Hamiltonians, with potential applications in molecular and material design. Furthermore, we introduce stabilizer thermodynamic systems as thermodynamic systems based on stabilizer codes, with the Hamiltonian constructed from a given code's stabilizer operators and the charges constructed from the code's logical operators. We benchmark the aforementioned algorithms on several examples of stabilizer thermodynamic systems, including those constructed from the one-to-three-qubit repetition code, the perfect one-to-five-qubit code, and the two-to-four-qubit error-detecting code. Finally, we observe that the aforementioned hybrid quantum-classical algorithms, when applied to stabilizer thermodynamic systems, can serve as alternative methods for encoding qubits into stabilizer codes at a fixed temperature, and we provide an effective method for warm-starting these encoding algorithms whenever a single qubit is encoded into multiple physical qubits.

Quantum thermodynamics and semi-definite optimization

In quantum thermodynamics, a system is described by a Hamiltonian and a list of non-commuting charges representing conserved quantities like particle number or electric charge, and an important goal is to determine the system's minimum energy in the presence of these conserved charges. In optimization theory, a semi-definite program (SDP) involves a linear objective function optimized over the cone of positive semi-definite operators intersected with an affine space. These problems arise from differing motivations in the physics and optimization communities and are phrased using very different terminology, yet they are essentially identical mathematically. By adopting Jaynes' mindset motivated by quantum thermodynamics, we observe that minimizing free energy in the aforementioned thermodynamics problem, instead of energy, leads to an elegant solution in terms of a dual chemical potential maximization problem that is concave in the chemical potential parameters. As such, one can employ standard (stochastic) gradient ascent methods to find the optimal values of these parameters, and these methods are guaranteed to converge quickly. At low temperature, the minimum free energy provides an excellent approximation for the minimum energy. We then show how this Jaynes-inspired gradient-ascent approach can be used in both first- and second-order classical and hybrid quantum-classical algorithms for minimizing energy, and equivalently, how it can be used for solving SDPs, with guarantees on the runtimes of the algorithms. The approach discussed here is well grounded in quantum thermodynamics and, as such, provides physical motivation underpinning why algorithms published fifty years after Jaynes' seminal work, including the matrix multiplicative weights update method, the matrix exponentiated gradient update method, and their quantum algorithmic generalizations, perform well at solving SDPs.

Sample complexity of quantum hypothesis testing

Quantum hypothesis testing has been traditionally studied from the information-theoretic perspective, wherein one is interested in the optimal decay rate of error probabilities as a function of the number of samples of an unknown state. In this paper, we study the sample complexity of quantum hypothesis testing, wherein the goal is to determine the minimum number of samples needed to reach a desired error probability. By making use of the wealth of knowledge that already exists in the literature on quantum hypothesis testing, we characterize the sample complexity of binary quantum hypothesis testing in the symmetric and asymmetric settings, and we provide bounds on the sample complexity of multiple quantum hypothesis testing. In more detail, we prove that the sample complexity of symmetric binary quantum hypothesis testing depends logarithmically on the inverse error probability and inversely on the negative logarithm of the fidelity. As a counterpart of the quantum Stein's lemma, we also find that the sample complexity of asymmetric binary quantum hypothesis testing depends logarithmically on the inverse type~II error probability and inversely on the quantum relative entropy. Finally, we provide lower and upper bounds on the sample complexity of multiple quantum hypothesis testing, with it remaining an intriguing open question to improve these bounds.

ClimSim: An open large-scale dataset for training high-resolution physics emulators in hybrid multi-scale climate simulators

Modern climate projections lack adequate spatial and temporal resolution due to computational constraints. A consequence is inaccurate and imprecise prediction of critical processes such as storms. Hybrid methods that combine physics with machine learning (ML) have introduced a new generation of higher fidelity climate simulators that can sidestep Moore's Law by outsourcing compute-hungry, short, high-resolution simulations to ML emulators. However, this hybrid ML-physics simulation approach requires domain-specific treatment and has been inaccessible to ML experts because of lack of training data and relevant, easy-to-use workflows. We present ClimSim, the largest-ever dataset designed for hybrid ML-physics research. It comprises multi-scale climate simulations, developed by a consortium of climate scientists and ML researchers. It consists of 5.7 billion pairs of multivariate input and output vectors that isolate the influence of locally-nested, high-resolution, high-fidelity physics on a host climate simulator's macro-scale physical state. The dataset is global in coverage, spans multiple years at high sampling frequency, and is designed such that resulting emulators are compatible with downstream coupling into operational climate simulators. We implement a range of deterministic and stochastic regression baselines to highlight the ML challenges and their scoring. The data (https://huggingface.co/datasets/LEAP/ClimSim_high-res) and code (https://leap-stc.github.io/ClimSim) are released openly to support the development of hybrid ML-physics and high-fidelity climate simulations for the benefit of science and society.

Optimal Provable Robustness of Quantum Classification via Quantum Hypothesis Testing

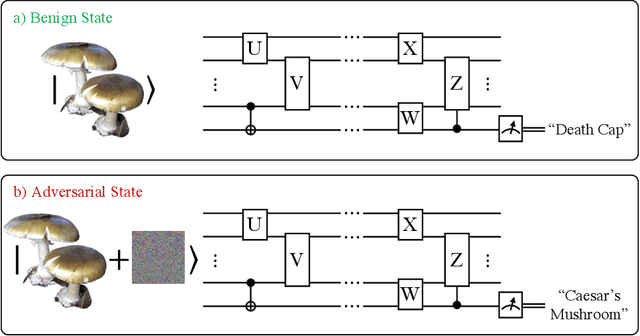
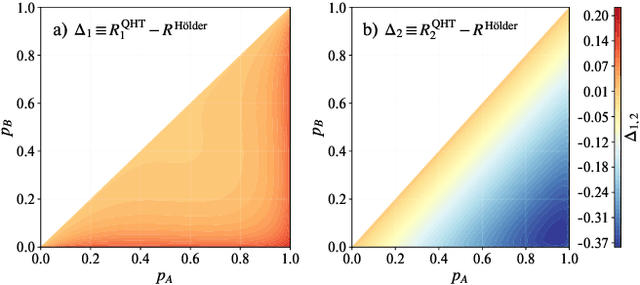
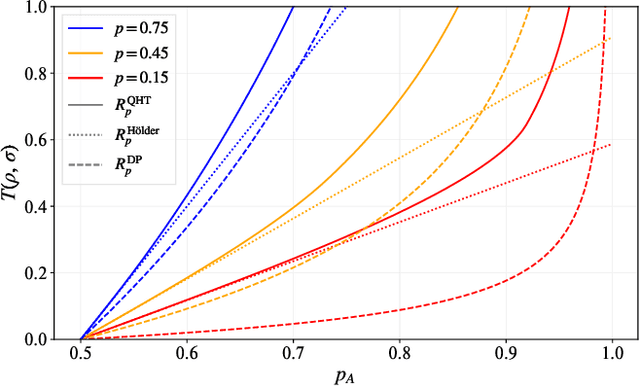
Quantum machine learning models have the potential to offer speedups and better predictive accuracy compared to their classical counterparts. However, these quantum algorithms, like their classical counterparts, have been shown to also be vulnerable to input perturbations, in particular for classification problems. These can arise either from noisy implementations or, as a worst-case type of noise, adversarial attacks. These attacks can undermine both the reliability and security of quantum classification algorithms. In order to develop defence mechanisms and to better understand the reliability of these algorithms, it is crucial to understand their robustness properties in presence of both natural noise sources and adversarial manipulation. From the observation that, unlike in the classical setting, measurements involved in quantum classification algorithms are naturally probabilistic, we uncover and formalize a fundamental link between binary quantum hypothesis testing (QHT) and provably robust quantum classification. Then from the optimality of QHT, we prove a robustness condition, which is tight under modest assumptions, and enables us to develop a protocol to certify robustness. Since this robustness condition is a guarantee against the worst-case noise scenarios, our result naturally extends to scenarios in which the noise source is known. Thus we also provide a framework to study the reliability of quantum classification protocols under more general settings.

Quantum noise protects quantum classifiers against adversaries

Noise in quantum information processing is often viewed as a disruptive and difficult-to-avoid feature, especially in near-term quantum technologies. However, noise has often played beneficial roles, from enhancing weak signals in stochastic resonance to protecting the privacy of data in differential privacy. It is then natural to ask, can we harness the power of quantum noise that is beneficial to quantum computing? An important current direction for quantum computing is its application to machine learning, such as classification problems. One outstanding problem in machine learning for classification is its sensitivity to adversarial examples. These are small, undetectable perturbations from the original data where the perturbed data is completely misclassified in otherwise extremely accurate classifiers. They can also be considered as `worst-case' perturbations by unknown noise sources. We show that by taking advantage of depolarisation noise in quantum circuits for classification, a robustness bound against adversaries can be derived where the robustness improves with increasing noise. This robustness property is intimately connected with an important security concept called differential privacy which can be extended to quantum differential privacy. For the protection of quantum data, this is the first quantum protocol that can be used against the most general adversaries. Furthermore, we show how the robustness in the classical case can be sensitive to the details of the classification model, but in the quantum case the details of classification model are absent, thus also providing a potential quantum advantage for classical data that is independent of quantum speedups. This opens the opportunity to explore other ways in which quantum noise can be used in our favour, as well as identifying other ways quantum algorithms can be helpful that is independent of quantum speedups.

Data Sanity Check for Deep Learning Systems via Learnt Assertions

Reliability is a critical consideration to DL-based systems. But the statistical nature of DL makes it quite vulnerable to invalid inputs, i.e., those cases that are not considered in the training phase of a DL model. This paper proposes to perform data sanity check to identify invalid inputs, so as to enhance the reliability of DL-based systems. We design and implement a tool to detect behavior deviation of a DL model when processing an input case. This tool extracts the data flow footprints and conducts an assertion-based validation mechanism. The assertions are built automatically, which are specifically-tailored for DL model data flow analysis. Our experiments conducted with real-world scenarios demonstrate that such an assertion-based data sanity check mechanism is effective in identifying invalid input cases.