Contraction of Private Quantum Channels and Private Quantum Hypothesis Testing

A quantum generalized divergence by definition satisfies the data-processing inequality; as such, the relative decrease in such a divergence under the action of a quantum channel is at most one. This relative decrease is formally known as the contraction coefficient of the channel and the divergence. Interestingly, there exist combinations of channels and divergences for which the contraction coefficient is strictly less than one. Furthermore, understanding the contraction coefficient is fundamental for the study of statistical tasks under privacy constraints. To this end, here we establish upper bounds on contraction coefficients for the hockey-stick divergence under privacy constraints, where privacy is quantified with respect to the quantum local differential privacy (QLDP) framework, and we fully characterize the contraction coefficient for the trace distance under privacy constraints. With the machinery developed, we also determine an upper bound on the contraction of both the Bures distance and quantum relative entropy relative to the normalized trace distance, under QLDP constraints. Next, we apply our findings to establish bounds on the sample complexity of quantum hypothesis testing under privacy constraints. Furthermore, we study various scenarios in which the sample complexity bounds are tight, while providing order-optimal quantum channels that achieve those bounds. Lastly, we show how private quantum channels provide fairness and Holevo information stability in quantum learning settings.

Sample complexity of quantum hypothesis testing

Quantum hypothesis testing has been traditionally studied from the information-theoretic perspective, wherein one is interested in the optimal decay rate of error probabilities as a function of the number of samples of an unknown state. In this paper, we study the sample complexity of quantum hypothesis testing, wherein the goal is to determine the minimum number of samples needed to reach a desired error probability. By making use of the wealth of knowledge that already exists in the literature on quantum hypothesis testing, we characterize the sample complexity of binary quantum hypothesis testing in the symmetric and asymmetric settings, and we provide bounds on the sample complexity of multiple quantum hypothesis testing. In more detail, we prove that the sample complexity of symmetric binary quantum hypothesis testing depends logarithmically on the inverse error probability and inversely on the negative logarithm of the fidelity. As a counterpart of the quantum Stein's lemma, we also find that the sample complexity of asymmetric binary quantum hypothesis testing depends logarithmically on the inverse type~II error probability and inversely on the quantum relative entropy. Finally, we provide lower and upper bounds on the sample complexity of multiple quantum hypothesis testing, with it remaining an intriguing open question to improve these bounds.

Quantum Pufferfish Privacy: A Flexible Privacy Framework for Quantum Systems

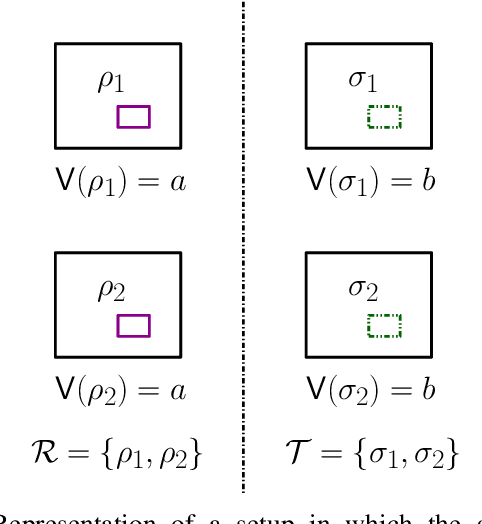
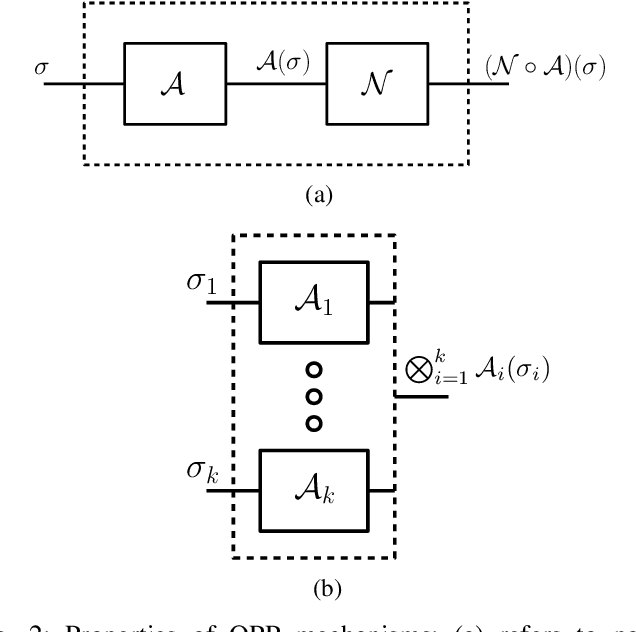
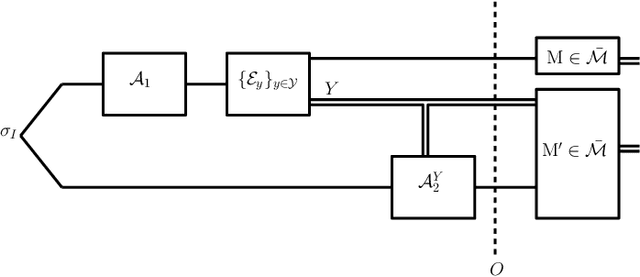
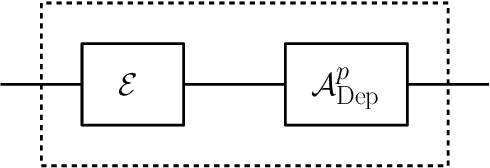
We propose a versatile privacy framework for quantum systems, termed quantum pufferfish privacy (QPP). Inspired by classical pufferfish privacy, our formulation generalizes and addresses limitations of quantum differential privacy by offering flexibility in specifying private information, feasible measurements, and domain knowledge. We show that QPP can be equivalently formulated in terms of the Datta-Leditzky information spectrum divergence, thus providing the first operational interpretation thereof. We reformulate this divergence as a semi-definite program and derive several properties of it, which are then used to prove convexity, composability, and post-processing of QPP mechanisms. Parameters that guarantee QPP of the depolarization mechanism are also derived. We analyze the privacy-utility tradeoff of general QPP mechanisms and, again, study the depolarization mechanism as an explicit instance. The QPP framework is then applied to privacy auditing for identifying privacy violations via a hypothesis testing pipeline that leverages quantum algorithms. Connections to quantum fairness and other quantum divergences are also explored and several variants of QPP are examined.

k-Sliced Mutual Information: A Quantitative Study of Scalability with Dimension

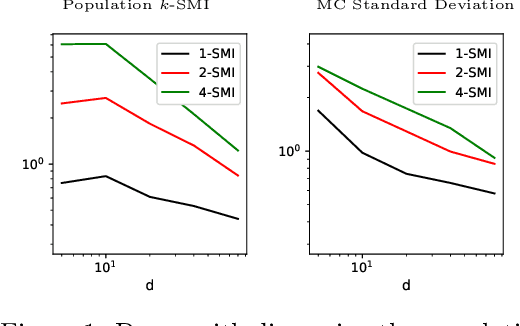
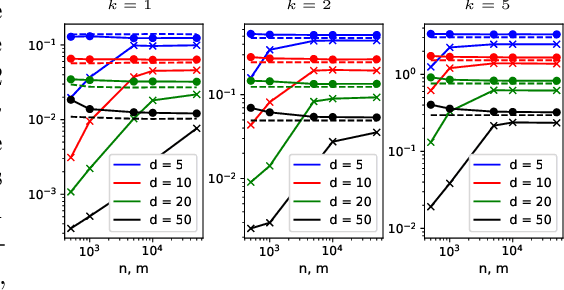
Sliced mutual information (SMI) is defined as an average of mutual information (MI) terms between one-dimensional random projections of the random variables. It serves as a surrogate measure of dependence to classic MI that preserves many of its properties but is more scalable to high dimensions. However, a quantitative characterization of how SMI itself and estimation rates thereof depend on the ambient dimension, which is crucial to the understanding of scalability, remain obscure. This works extends the original SMI definition to $k$-SMI, which considers projections to $k$-dimensional subspaces, and provides a multifaceted account on its dependence on dimension. Using a new result on the continuity of differential entropy in the 2-Wasserstein metric, we derive sharp bounds on the error of Monte Carlo (MC)-based estimates of $k$-SMI, with explicit dependence on $k$ and the ambient dimension, revealing their interplay with the number of samples. We then combine the MC integrator with the neural estimation framework to provide an end-to-end $k$-SMI estimator, for which optimal convergence rates are established. We also explore asymptotics of the population $k$-SMI as dimension grows, providing Gaussian approximation results with a residual that decays under appropriate moment bounds. Our theory is validated with numerical experiments and is applied to sliced InfoGAN, which altogether provide a comprehensive quantitative account of the scalability question of $k$-SMI, including SMI as a special case when $k=1$.