Quantum Doeblin Coefficients: Interpretations and Applications

In classical information theory, the Doeblin coefficient of a classical channel provides an efficiently computable upper bound on the total-variation contraction coefficient of the channel, leading to what is known as a strong data-processing inequality. Here, we investigate quantum Doeblin coefficients as a generalization of the classical concept. In particular, we define various new quantum Doeblin coefficients, one of which has several desirable properties, including concatenation and multiplicativity, in addition to being efficiently computable. We also develop various interpretations of two of the quantum Doeblin coefficients, including representations as minimal singlet fractions, exclusion values, reverse max-mutual and oveloH informations, reverse robustnesses, and hypothesis testing reverse mutual and oveloH informations. Our interpretations of quantum Doeblin coefficients as either entanglement-assisted or unassisted exclusion values are particularly appealing, indicating that they are proportional to the best possible error probabilities one could achieve in state-exclusion tasks by making use of the channel. We also outline various applications of quantum Doeblin coefficients, ranging from limitations on quantum machine learning algorithms that use parameterized quantum circuits (noise-induced barren plateaus), on error mitigation protocols, on the sample complexity of noisy quantum hypothesis testing, on the fairness of noisy quantum models, and on mixing times of time-varying channels. All of these applications make use of the fact that quantum Doeblin coefficients appear in upper bounds on various trace-distance contraction coefficients of a channel. Furthermore, in all of these applications, our analysis using Doeblin coefficients provides improvements of various kinds over contributions from prior literature, both in terms of generality and being efficiently computable.

Quantum Normalizing Flows for Anomaly Detection

A Normalizing Flow computes a bijective mapping from an arbitrary distribution to a predefined (e.g. normal) distribution. Such a flow can be used to address different tasks, e.g. anomaly detection, once such a mapping has been learned. In this work we introduce Normalizing Flows for Quantum architectures, describe how to model and optimize such a flow and evaluate our method on example datasets. Our proposed models show competitive performance for anomaly detection compared to classical methods, e.g. based on isolation forests, the local outlier factor (LOF) or single-class SVMs, while being fully executable on a quantum computer.

Quantum Differential Privacy: An Information Theory Perspective

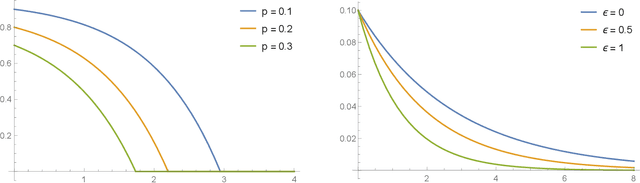
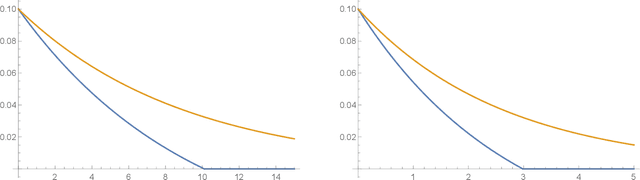
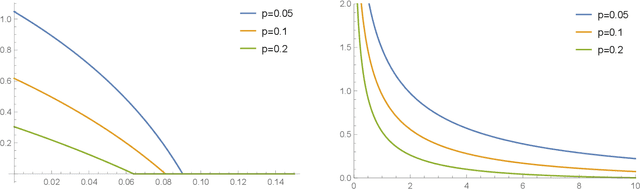
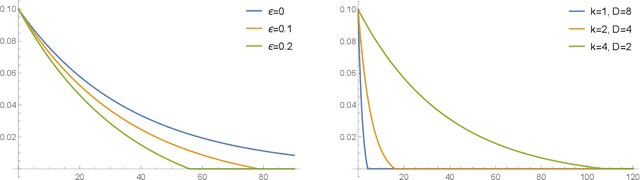
Differential privacy has been an exceptionally successful concept when it comes to providing provable security guarantees for classical computations. More recently, the concept was generalized to quantum computations. While classical computations are essentially noiseless and differential privacy is often achieved by artificially adding noise, near-term quantum computers are inherently noisy and it was observed that this leads to natural differential privacy as a feature. In this work we discuss quantum differential privacy in an information theoretic framework by casting it as a quantum divergence. A main advantage of this approach is that differential privacy becomes a property solely based on the output states of the computation, without the need to check it for every measurement. This leads to simpler proofs and generalized statements of its properties as well as several new bounds for both, general and specific, noise models. In particular, these include common representations of quantum circuits and quantum machine learning concepts. Here, we focus on the difference in the amount of noise required to achieve certain levels of differential privacy versus the amount that would make any computation useless. Finally, we also generalize the classical concepts of local differential privacy, R\'enyi differential privacy and the hypothesis testing interpretation to the quantum setting, providing several new properties and insights.