Gradient Flows and Riemannian Structure in the Gromov-Wasserstein Geometry

The Wasserstein space of probability measures is known for its intricate Riemannian structure, which underpins the Wasserstein geometry and enables gradient flow algorithms. However, the Wasserstein geometry may not be suitable for certain tasks or data modalities. Motivated by scenarios where the global structure of the data needs to be preserved, this work initiates the study of gradient flows and Riemannian structure in the Gromov-Wasserstein (GW) geometry, which is particularly suited for such purposes. We focus on the inner product GW (IGW) distance between distributions on $\mathbb{R}^d$. Given a functional $\mathsf{F}:\mathcal{P}_2(\mathbb{R}^d)\to\mathbb{R}$ to optimize, we present an implicit IGW minimizing movement scheme that generates a sequence of distributions $\{\rho_i\}_{i=0}^n$, which are close in IGW and aligned in the 2-Wasserstein sense. Taking the time step to zero, we prove that the discrete solution converges to an IGW generalized minimizing movement (GMM) $(\rho_t)_t$ that follows the continuity equation with a velocity field $v_t\in L^2(\rho_t;\mathbb{R}^d)$, specified by a global transformation of the Wasserstein gradient of $\mathsf{F}$. The transformation is given by a mobility operator that modifies the Wasserstein gradient to encode not only local information, but also global structure. Our gradient flow analysis leads us to identify the Riemannian structure that gives rise to the intrinsic IGW geometry, using which we establish a Benamou-Brenier-like formula for IGW. We conclude with a formal derivation, akin to the Otto calculus, of the IGW gradient as the inverse mobility acting on the Wasserstein gradient. Numerical experiments validating our theory and demonstrating the global nature of IGW interpolations are provided.

Robust Distribution Learning with Local and Global Adversarial Corruptions

We consider learning in an adversarial environment, where an $\varepsilon$-fraction of samples from a distribution $P$ are arbitrarily modified (*global* corruptions) and the remaining perturbations have average magnitude bounded by $\rho$ (*local* corruptions). Given access to $n$ such corrupted samples, we seek a computationally efficient estimator $\hat{P}_n$ that minimizes the Wasserstein distance $\mathsf{W}_1(\hat{P}_n,P)$. In fact, we attack the fine-grained task of minimizing $\mathsf{W}_1(\Pi_\# \hat{P}_n, \Pi_\# P)$ for all orthogonal projections $\Pi \in \mathbb{R}^{d \times d}$, with performance scaling with $\mathrm{rank}(\Pi) = k$. This allows us to account simultaneously for mean estimation ($k=1$), distribution estimation ($k=d$), as well as the settings interpolating between these two extremes. We characterize the optimal population-limit risk for this task and then develop an efficient finite-sample algorithm with error bounded by $\sqrt{\varepsilon k} + \rho + d^{O(1)}\tilde{O}(n^{-1/k})$ when $P$ has bounded moments of order $2+\delta$, for constant $\delta > 0$. For data distributions with bounded covariance, our finite-sample bounds match the minimax population-level optimum for large sample sizes. Our efficient procedure relies on a novel trace norm approximation of an ideal yet intractable 2-Wasserstein projection estimator. We apply this algorithm to robust stochastic optimization, and, in the process, uncover a new method for overcoming the curse of dimensionality in Wasserstein distributionally robust optimization.

Information-Theoretic Generalization Bounds for Deep Neural Networks

Deep neural networks (DNNs) exhibit an exceptional capacity for generalization in practical applications. This work aims to capture the effect and benefits of depth for supervised learning via information-theoretic generalization bounds. We first derive two hierarchical bounds on the generalization error in terms of the Kullback-Leibler (KL) divergence or the 1-Wasserstein distance between the train and test distributions of the network internal representations. The KL divergence bound shrinks as the layer index increases, while the Wasserstein bound implies the existence of a layer that serves as a generalization funnel, which attains a minimal 1-Wasserstein distance. Analytic expressions for both bounds are derived under the setting of binary Gaussian classification with linear DNNs. To quantify the contraction of the relevant information measures when moving deeper into the network, we analyze the strong data processing inequality (SDPI) coefficient between consecutive layers of three regularized DNN models: Dropout, DropConnect, and Gaussian noise injection. This enables refining our generalization bounds to capture the contraction as a function of the network architecture parameters. Specializing our results to DNNs with a finite parameter space and the Gibbs algorithm reveals that deeper yet narrower network architectures generalize better in those examples, although how broadly this statement applies remains a question.

Outlier-Robust Wasserstein DRO

Distributionally robust optimization (DRO) is an effective approach for data-driven decision-making in the presence of uncertainty. Geometric uncertainty due to sampling or localized perturbations of data points is captured by Wasserstein DRO (WDRO), which seeks to learn a model that performs uniformly well over a Wasserstein ball centered around the observed data distribution. However, WDRO fails to account for non-geometric perturbations such as adversarial outliers, which can greatly distort the Wasserstein distance measurement and impede the learned model. We address this gap by proposing a novel outlier-robust WDRO framework for decision-making under both geometric (Wasserstein) perturbations and non-geometric (total variation (TV)) contamination that allows an $\varepsilon$-fraction of data to be arbitrarily corrupted. We design an uncertainty set using a certain robust Wasserstein ball that accounts for both perturbation types and derive minimax optimal excess risk bounds for this procedure that explicitly capture the Wasserstein and TV risks. We prove a strong duality result that enables tractable convex reformulations and efficient computation of our outlier-robust WDRO problem. When the loss function depends only on low-dimensional features of the data, we eliminate certain dimension dependencies from the risk bounds that are unavoidable in the general setting. Finally, we present experiments validating our theory on standard regression and classification tasks.

Max-Sliced Mutual Information

Quantifying the dependence between high-dimensional random variables is central to statistical learning and inference. Two classical methods are canonical correlation analysis (CCA), which identifies maximally correlated projected versions of the original variables, and Shannon's mutual information, which is a universal dependence measure that also captures high-order dependencies. However, CCA only accounts for linear dependence, which may be insufficient for certain applications, while mutual information is often infeasible to compute/estimate in high dimensions. This work proposes a middle ground in the form of a scalable information-theoretic generalization of CCA, termed max-sliced mutual information (mSMI). mSMI equals the maximal mutual information between low-dimensional projections of the high-dimensional variables, which reduces back to CCA in the Gaussian case. It enjoys the best of both worlds: capturing intricate dependencies in the data while being amenable to fast computation and scalable estimation from samples. We show that mSMI retains favorable structural properties of Shannon's mutual information, like variational forms and identification of independence. We then study statistical estimation of mSMI, propose an efficiently computable neural estimator, and couple it with formal non-asymptotic error bounds. We present experiments that demonstrate the utility of mSMI for several tasks, encompassing independence testing, multi-view representation learning, algorithmic fairness, and generative modeling. We observe that mSMI consistently outperforms competing methods with little-to-no computational overhead.

Quantum Neural Estimation of Entropies

Entropy measures quantify the amount of information and correlations present in a quantum system. In practice, when the quantum state is unknown and only copies thereof are available, one must resort to the estimation of such entropy measures. Here we propose a variational quantum algorithm for estimating the von Neumann and R\'enyi entropies, as well as the measured relative entropy and measured R\'enyi relative entropy. Our approach first parameterizes a variational formula for the measure of interest by a quantum circuit and a classical neural network, and then optimizes the resulting objective over parameter space. Numerical simulations of our quantum algorithm are provided, using a noiseless quantum simulator. The algorithm provides accurate estimates of the various entropy measures for the examples tested, which renders it as a promising approach for usage in downstream tasks.

Quantum Pufferfish Privacy: A Flexible Privacy Framework for Quantum Systems

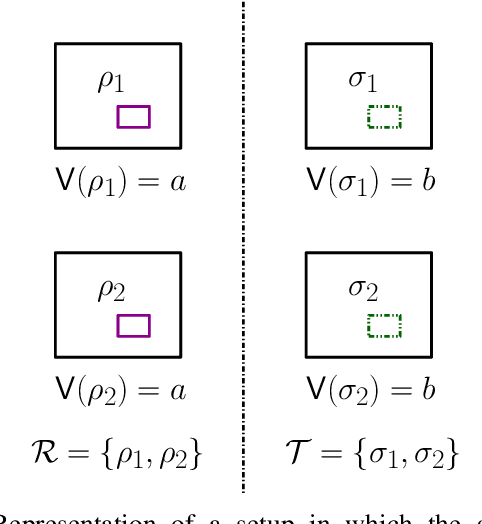
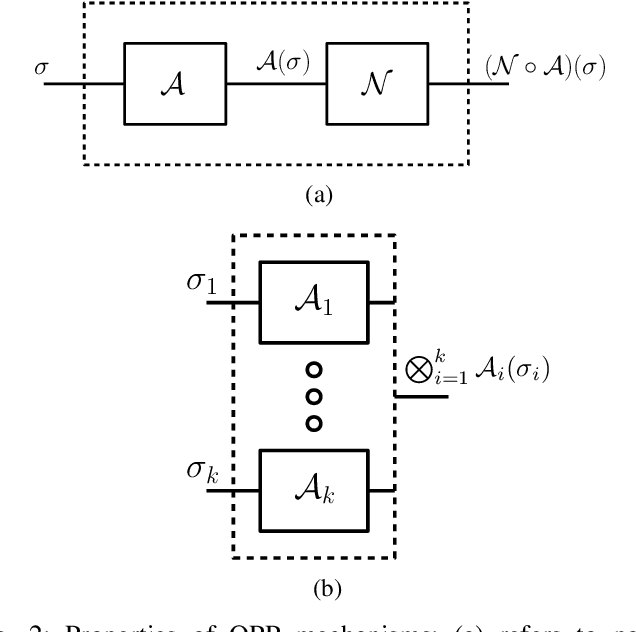
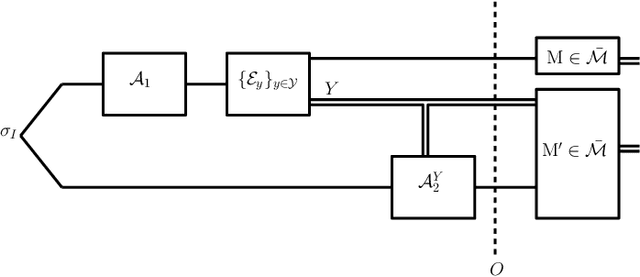
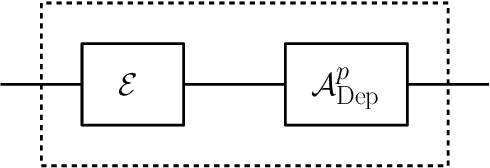
We propose a versatile privacy framework for quantum systems, termed quantum pufferfish privacy (QPP). Inspired by classical pufferfish privacy, our formulation generalizes and addresses limitations of quantum differential privacy by offering flexibility in specifying private information, feasible measurements, and domain knowledge. We show that QPP can be equivalently formulated in terms of the Datta-Leditzky information spectrum divergence, thus providing the first operational interpretation thereof. We reformulate this divergence as a semi-definite program and derive several properties of it, which are then used to prove convexity, composability, and post-processing of QPP mechanisms. Parameters that guarantee QPP of the depolarization mechanism are also derived. We analyze the privacy-utility tradeoff of general QPP mechanisms and, again, study the depolarization mechanism as an explicit instance. The QPP framework is then applied to privacy auditing for identifying privacy violations via a hypothesis testing pipeline that leverages quantum algorithms. Connections to quantum fairness and other quantum divergences are also explored and several variants of QPP are examined.

Robust Estimation under the Wasserstein Distance

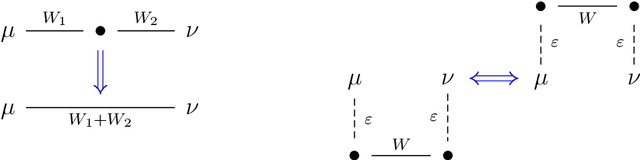
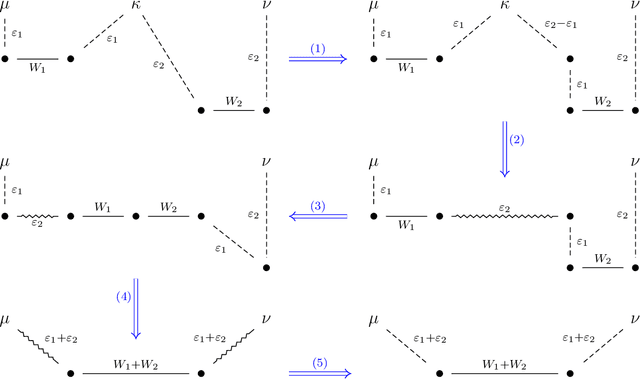
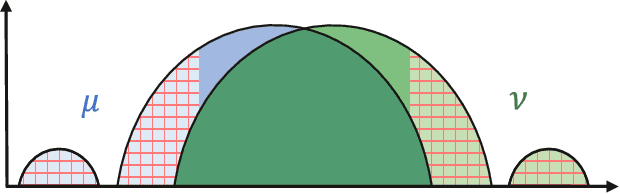
We study the problem of robust distribution estimation under the Wasserstein metric, a popular discrepancy measure between probability distributions rooted in optimal transport (OT) theory. We introduce a new outlier-robust Wasserstein distance $\mathsf{W}_p^\varepsilon$ which allows for $\varepsilon$ outlier mass to be removed from its input distributions, and show that minimum distance estimation under $\mathsf{W}_p^\varepsilon$ achieves minimax optimal robust estimation risk. Our analysis is rooted in several new results for partial OT, including an approximate triangle inequality, which may be of independent interest. To address computational tractability, we derive a dual formulation for $\mathsf{W}_p^\varepsilon$ that adds a simple penalty term to the classic Kantorovich dual objective. As such, $\mathsf{W}_p^\varepsilon$ can be implemented via an elementary modification to standard, duality-based OT solvers. Our results are extended to sliced OT, where distributions are projected onto low-dimensional subspaces, and applications to homogeneity and independence testing are explored. We illustrate the virtues of our framework via applications to generative modeling with contaminated datasets.

Data-Driven Optimization of Directed Information over Discrete Alphabets

Directed information (DI) is a fundamental measure for the study and analysis of sequential stochastic models. In particular, when optimized over input distributions it characterizes the capacity of general communication channels. However, analytic computation of DI is typically intractable and existing optimization techniques over discrete input alphabets require knowledge of the channel model, which renders them inapplicable when only samples are available. To overcome these limitations, we propose a novel estimation-optimization framework for DI over discrete input spaces. We formulate DI optimization as a Markov decision process and leverage reinforcement learning techniques to optimize a deep generative model of the input process probability mass function (PMF). Combining this optimizer with the recently developed DI neural estimator, we obtain an end-to-end estimation-optimization algorithm which is applied to estimating the (feedforward and feedback) capacity of various discrete channels with memory. Furthermore, we demonstrate how to use the optimized PMF model to (i) obtain theoretical bounds on the feedback capacity of unifilar finite-state channels; and (ii) perform probabilistic shaping of constellations in the peak power-constrained additive white Gaussian noise channel.

Statistical, Robustness, and Computational Guarantees for Sliced Wasserstein Distances

Sliced Wasserstein distances preserve properties of classic Wasserstein distances while being more scalable for computation and estimation in high dimensions. The goal of this work is to quantify this scalability from three key aspects: (i) empirical convergence rates; (ii) robustness to data contamination; and (iii) efficient computational methods. For empirical convergence, we derive fast rates with explicit dependence of constants on dimension, subject to log-concavity of the population distributions. For robustness, we characterize minimax optimal, dimension-free robust estimation risks, and show an equivalence between robust sliced 1-Wasserstein estimation and robust mean estimation. This enables lifting statistical and algorithmic guarantees available for the latter to the sliced 1-Wasserstein setting. Moving on to computational aspects, we analyze the Monte Carlo estimator for the average-sliced distance, demonstrating that larger dimension can result in faster convergence of the numerical integration error. For the max-sliced distance, we focus on a subgradient-based local optimization algorithm that is frequently used in practice, albeit without formal guarantees, and establish an $O(\epsilon^{-4})$ computational complexity bound for it. Our theory is validated by numerical experiments, which altogether provide a comprehensive quantitative account of the scalability question.