The Limits of Transfer Reinforcement Learning with Latent Low-rank Structure

Many reinforcement learning (RL) algorithms are too costly to use in practice due to the large sizes $S, A$ of the problem's state and action space. To resolve this issue, we study transfer RL with latent low rank structure. We consider the problem of transferring a latent low rank representation when the source and target MDPs have transition kernels with Tucker rank $(S , d, A )$, $(S , S , d), (d, S, A )$, or $(d , d , d )$. In each setting, we introduce the transfer-ability coefficient $\alpha$ that measures the difficulty of representational transfer. Our algorithm learns latent representations in each source MDP and then exploits the linear structure to remove the dependence on $S, A $, or $S A$ in the target MDP regret bound. We complement our positive results with information theoretic lower bounds that show our algorithms (excluding the ($d, d, d$) setting) are minimax-optimal with respect to $\alpha$.

Entry-Specific Matrix Estimation under Arbitrary Sampling Patterns through the Lens of Network Flows

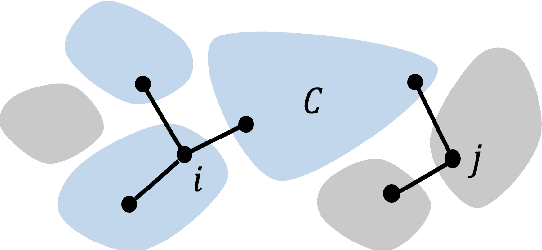
Matrix completion tackles the task of predicting missing values in a low-rank matrix based on a sparse set of observed entries. It is often assumed that the observation pattern is generated uniformly at random or has a very specific structure tuned to a given algorithm. There is still a gap in our understanding when it comes to arbitrary sampling patterns. Given an arbitrary sampling pattern, we introduce a matrix completion algorithm based on network flows in the bipartite graph induced by the observation pattern. For additive matrices, the particular flow we used is the electrical flow and we establish error upper bounds customized to each entry as a function of the observation set, along with matching minimax lower bounds. Our results show that the minimax squared error for recovery of a particular entry in the matrix is proportional to the effective resistance of the corresponding edge in the graph. Furthermore, we show that our estimator is equivalent to the least squares estimator. We apply our estimator to the two-way fixed effects model and show that it enables us to accurately infer individual causal effects and the unit-specific and time-specific confounders. For rank-$1$ matrices, we use edge-disjoint paths to form an estimator that achieves minimax optimal estimation when the sampling is sufficiently dense. Our discovery introduces a new family of estimators parametrized by network flows, which provide a fine-grained and intuitive understanding of the impact of the given sampling pattern on the relative difficulty of estimation at an entry-specific level. This graph-based approach allows us to quantify the inherent complexity of matrix completion for individual entries, rather than relying solely on global measures of performance.

Information-Theoretic Generalization Bounds for Deep Neural Networks

Deep neural networks (DNNs) exhibit an exceptional capacity for generalization in practical applications. This work aims to capture the effect and benefits of depth for supervised learning via information-theoretic generalization bounds. We first derive two hierarchical bounds on the generalization error in terms of the Kullback-Leibler (KL) divergence or the 1-Wasserstein distance between the train and test distributions of the network internal representations. The KL divergence bound shrinks as the layer index increases, while the Wasserstein bound implies the existence of a layer that serves as a generalization funnel, which attains a minimal 1-Wasserstein distance. Analytic expressions for both bounds are derived under the setting of binary Gaussian classification with linear DNNs. To quantify the contraction of the relevant information measures when moving deeper into the network, we analyze the strong data processing inequality (SDPI) coefficient between consecutive layers of three regularized DNN models: Dropout, DropConnect, and Gaussian noise injection. This enables refining our generalization bounds to capture the contraction as a function of the network architecture parameters. Specializing our results to DNNs with a finite parameter space and the Gibbs algorithm reveals that deeper yet narrower network architectures generalize better in those examples, although how broadly this statement applies remains a question.

Entry-Specific Bounds for Low-Rank Matrix Completion under Highly Non-Uniform Sampling

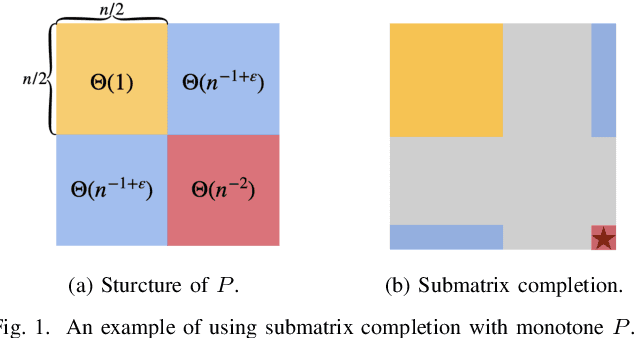
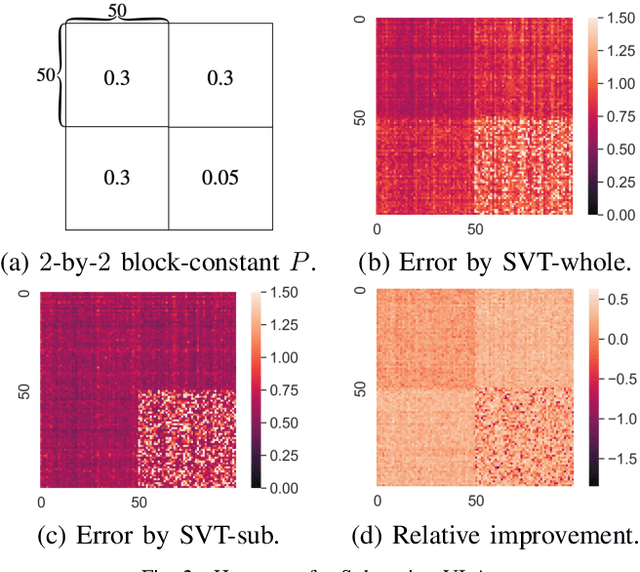
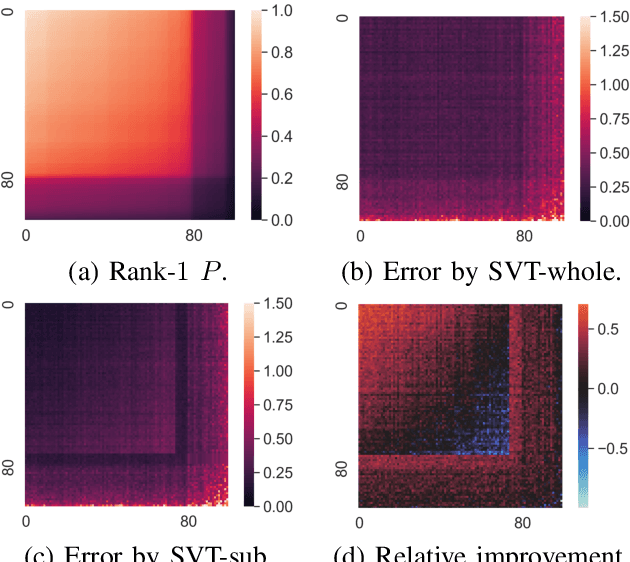
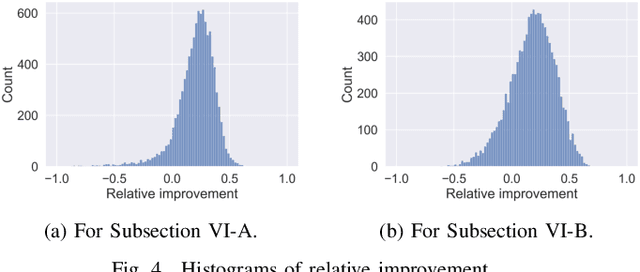
Low-rank matrix completion concerns the problem of estimating unobserved entries in a matrix using a sparse set of observed entries. We consider the non-uniform setting where the observed entries are sampled with highly varying probabilities, potentially with different asymptotic scalings. We show that under structured sampling probabilities, it is often better and sometimes optimal to run estimation algorithms on a smaller submatrix rather than the entire matrix. In particular, we prove error upper bounds customized to each entry, which match the minimax lower bounds under certain conditions. Our bounds characterize the hardness of estimating each entry as a function of the localized sampling probabilities. We provide numerical experiments that confirm our theoretical findings.

The SMART approach to instance-optimal online learning

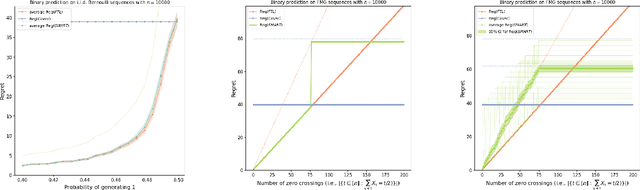
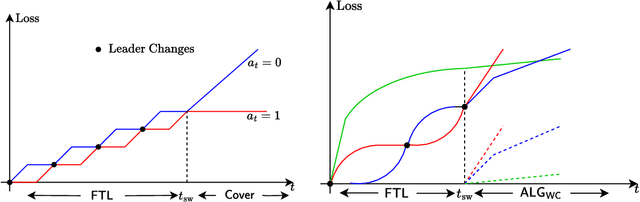
We devise an online learning algorithm -- titled Switching via Monotone Adapted Regret Traces (SMART) -- that adapts to the data and achieves regret that is instance optimal, i.e., simultaneously competitive on every input sequence compared to the performance of the follow-the-leader (FTL) policy and the worst case guarantee of any other input policy. We show that the regret of the SMART policy on any input sequence is within a multiplicative factor $e/(e-1) \approx 1.58$ of the smaller of: 1) the regret obtained by FTL on the sequence, and 2) the upper bound on regret guaranteed by the given worst-case policy. This implies a strictly stronger guarantee than typical `best-of-both-worlds' bounds as the guarantee holds for every input sequence regardless of how it is generated. SMART is simple to implement as it begins by playing FTL and switches at most once during the time horizon to the worst-case algorithm. Our approach and results follow from an operational reduction of instance optimal online learning to competitive analysis for the ski-rental problem. We complement our competitive ratio upper bounds with a fundamental lower bound showing that over all input sequences, no algorithm can get better than a $1.43$-fraction of the minimum regret achieved by FTL and the minimax-optimal policy. We also present a modification of SMART that combines FTL with a ``small-loss" algorithm to achieve instance optimality between the regret of FTL and the small loss regret bound.

Faster Rates for Switchback Experiments

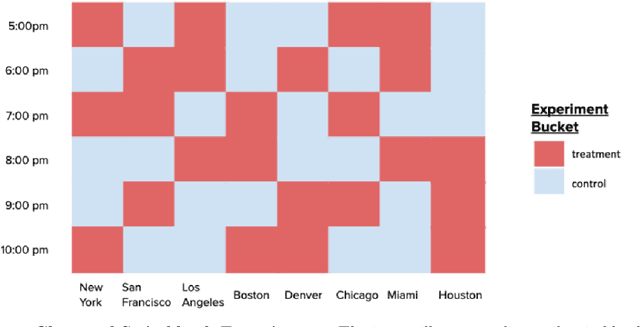
Switchback experimental design, wherein a single unit (e.g., a whole system) is exposed to a single random treatment for interspersed blocks of time, tackles both cross-unit and temporal interference. Hu and Wager (2022) recently proposed a treatment-effect estimator that truncates the beginnings of blocks and established a $T^{-1/3}$ rate for estimating the global average treatment effect (GATE) in a Markov setting with rapid mixing. They claim this rate is optimal and suggest focusing instead on a different (and design-dependent) estimand so as to enjoy a faster rate. For the same design we propose an alternative estimator that uses the whole block and surprisingly show that it in fact achieves an estimation rate of $\sqrt{\log T/T}$ for the original design-independent GATE estimand under the same assumptions.

Matrix Estimation for Offline Reinforcement Learning with Low-Rank Structure

We consider offline Reinforcement Learning (RL), where the agent does not interact with the environment and must rely on offline data collected using a behavior policy. Previous works provide policy evaluation guarantees when the target policy to be evaluated is covered by the behavior policy, that is, state-action pairs visited by the target policy must also be visited by the behavior policy. We show that when the MDP has a latent low-rank structure, this coverage condition can be relaxed. Building on the connection to weighted matrix completion with non-uniform observations, we propose an offline policy evaluation algorithm that leverages the low-rank structure to estimate the values of uncovered state-action pairs. Our algorithm does not require a known feature representation, and our finite-sample error bound involves a novel discrepancy measure quantifying the discrepancy between the behavior and target policies in the spectral space. We provide concrete examples where our algorithm achieves accurate estimation while existing coverage conditions are not satisfied. Building on the above evaluation algorithm, we further design an offline policy optimization algorithm and provide non-asymptotic performance guarantees.

Network Synthetic Interventions: A Framework for Panel Data with Network Interference

We propose a generalization of the synthetic controls and synthetic interventions methodology to incorporate network interference. We consider the estimation of unit-specific treatment effects from panel data where there are spillover effects across units and in the presence of unobserved confounding. Key to our approach is a novel latent factor model that takes into account network interference and generalizes the factor models typically used in panel data settings. We propose an estimator, "network synthetic interventions", and show that it consistently estimates the mean outcomes for a unit under an arbitrary sequence of treatments for itself and its neighborhood, given certain observation patterns hold in the data. We corroborate our theoretical findings with simulations.

Artificial Replay: A Meta-Algorithm for Harnessing Historical Data in Bandits

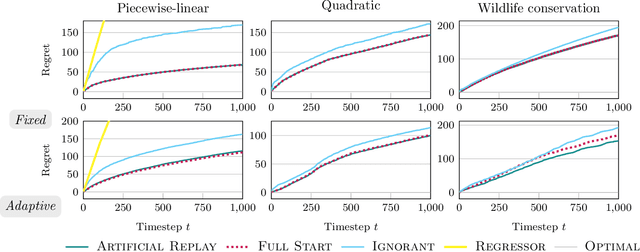
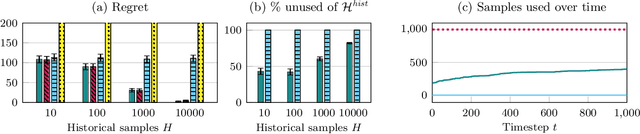
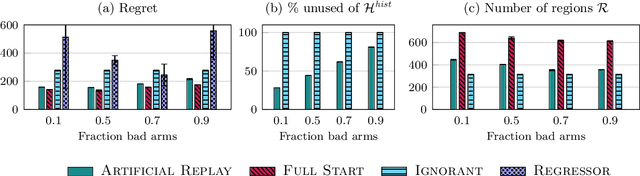
While standard bandit algorithms sometimes incur high regret, their performance can be greatly improved by "warm starting" with historical data. Unfortunately, how best to incorporate historical data is unclear: naively initializing reward estimates using all historical samples can suffer from spurious data and imbalanced data coverage, leading to computational and storage issues - particularly in continuous action spaces. We address these two challenges by proposing Artificial Replay, a meta-algorithm for incorporating historical data into any arbitrary base bandit algorithm. Artificial Replay uses only a subset of the historical data as needed to reduce computation and storage. We show that for a broad class of base algorithms that satisfy independence of irrelevant data (IIData), a novel property that we introduce, our method achieves equal regret as a full warm-start approach while potentially using only a fraction of the historical data. We complement these theoretical results with a case study of $K$-armed and continuous combinatorial bandit algorithms, including on a green security domain using real poaching data, to show the practical benefits of Artificial Replay in achieving optimal regret alongside low computational and storage costs.

Overcoming the Long Horizon Barrier for Sample-Efficient Reinforcement Learning with Latent Low-Rank Structure

The practicality of reinforcement learning algorithms has been limited due to poor scaling with respect to the problem size, as the sample complexity of learning an $\epsilon$-optimal policy is $\Tilde{\Omega}\left(|S||A|H^3 / \eps^2\right)$ over worst case instances of an MDP with state space $S$, action space $A$, and horizon $H$. We consider a class of MDPs that exhibit low rank structure, where the latent features are unknown. We argue that a natural combination of value iteration and low-rank matrix estimation results in an estimation error that grows doubly exponentially in the horizon $H$. We then provide a new algorithm along with statistical guarantees that efficiently exploits low rank structure given access to a generative model, achieving a sample complexity of $\Tilde{O}\left(d^5(|S|+|A|)\mathrm{poly}(H)/\eps^2\right)$ for a rank $d$ setting, which is minimax optimal with respect to the scaling of $|S|, |A|$, and $\eps$. In contrast to literature on linear and low-rank MDPs, we do not require a known feature mapping, our algorithm is computationally simple, and our results hold for long time horizons. Our results provide insights on the minimal low-rank structural assumptions required on the MDP with respect to the transition kernel versus the optimal action-value function.