Non-Stationary Inventory Control with Lead Times

We study non-stationary single-item, periodic-review inventory control problems in which the demand distribution is unknown and may change over time. We analyze how demand non-stationarity affects learning performance across inventory models, including systems with demand backlogging or lost-sales, both with and without lead times. For each setting, we propose an adaptive online algorithm that optimizes over the class of base-stock policies and establish performance guarantees in terms of dynamic regret relative to the optimal base-stock policy at each time step. Our results reveal a sharp separation across inventory models. In backlogging systems and lost-sales models with zero lead time, we show that it is possible to adapt to demand changes without incurring additional performance loss in stationary environments, even without prior knowledge of the demand distributions or the number of demand shifts. In contrast, for lost-sales systems with positive lead times, we establish weaker guarantees that reflect fundamental limitations imposed by delayed replenishment in combination with censored feedback. Our algorithms leverage the convexity and one-sided feedback structure of inventory costs to enable counterfactual policy evaluation despite demand censoring. We complement the theoretical analysis with simulation results showing that our methods significantly outperform existing benchmarks.

Is Pure Exploitation Sufficient in Exogenous MDPs with Linear Function Approximation?

Exogenous MDPs (Exo-MDPs) capture sequential decision-making where uncertainty comes solely from exogenous inputs that evolve independently of the learner's actions. This structure is especially common in operations research applications such as inventory control, energy storage, and resource allocation, where exogenous randomness (e.g., demand, arrivals, or prices) drives system behavior. Despite decades of empirical evidence that greedy, exploitation-only methods work remarkably well in these settings, theory has lagged behind: all existing regret guarantees for Exo-MDPs rely on explicit exploration or tabular assumptions. We show that exploration is unnecessary. We propose Pure Exploitation Learning (PEL) and prove the first general finite-sample regret bounds for exploitation-only algorithms in Exo-MDPs. In the tabular case, PEL achieves $\widetilde{O}(H^2|Ξ|\sqrt{K})$. For large, continuous endogenous state spaces, we introduce LSVI-PE, a simple linear-approximation method whose regret is polynomial in the feature dimension, exogenous state space, and horizon, independent of the endogenous state and action spaces. Our analysis introduces two new tools: counterfactual trajectories and Bellman-closed feature transport, which together allow greedy policies to have accurate value estimates without optimism. Experiments on synthetic and resource-management tasks show that PEL consistently outperforming baselines. Overall, our results overturn the conventional wisdom that exploration is required, demonstrating that in Exo-MDPs, pure exploitation is enough.

Reinforcement Learning in MDPs with Information-Ordered Policies

We propose an epoch-based reinforcement learning algorithm for infinite-horizon average-cost Markov decision processes (MDPs) that leverages a partial order over a policy class. In this structure, $\pi' \leq \pi$ if data collected under $\pi$ can be used to estimate the performance of $\pi'$, enabling counterfactual inference without additional environment interaction. Leveraging this partial order, we show that our algorithm achieves a regret bound of $O(\sqrt{w \log(|\Theta|) T})$, where $w$ is the width of the partial order. Notably, the bound is independent of the state and action space sizes. We illustrate the applicability of these partial orders in many domains in operations research, including inventory control and queuing systems. For each, we apply our framework to that problem, yielding new theoretical guarantees and strong empirical results without imposing extra assumptions such as convexity in the inventory model or specialized arrival-rate structure in the queuing model.

The Data-Driven Censored Newsvendor Problem

We study a censored variant of the data-driven newsvendor problem, where the decision-maker must select an ordering quantity that minimizes expected overage and underage costs based only on censored sales data, rather than historical demand realizations. To isolate the impact of demand censoring on this problem, we adopt a distributionally robust optimization framework, evaluating policies according to their worst-case regret over an ambiguity set of distributions. This set is defined by the largest historical order quantity (the observable boundary of the dataset), and contains all distributions matching the true demand distribution up to this boundary, while allowing them to be arbitrary afterwards. We demonstrate a spectrum of achievability under demand censoring by deriving a natural necessary and sufficient condition under which vanishing regret is an achievable goal. In regimes in which it is not, we exactly characterize the information loss due to censoring: an insurmountable lower bound on the performance of any policy, even when the decision-maker has access to infinitely many demand samples. We then leverage these sharp characterizations to propose a natural robust algorithm that adapts to the historical level of demand censoring. We derive finite-sample guarantees for this algorithm across all possible censoring regimes, and show its near-optimality with matching lower bounds (up to polylogarithmic factors). We moreover demonstrate its robust performance via extensive numerical experiments on both synthetic and real-world datasets.

Exploiting Exogenous Structure for Sample-Efficient Reinforcement Learning

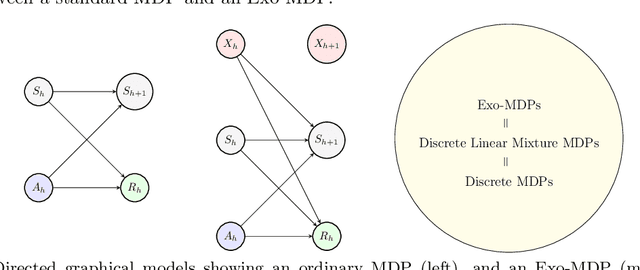
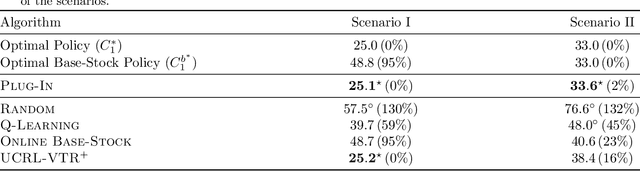
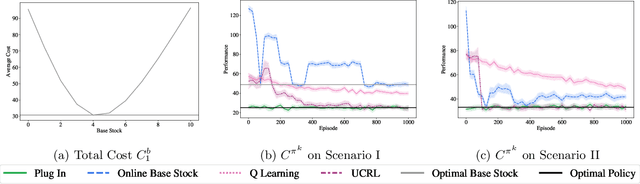
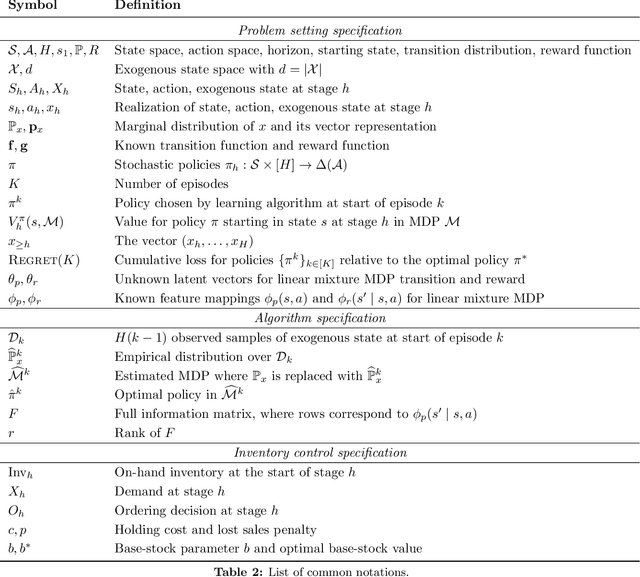
We study a class of structured Markov Decision Processes (MDPs) known as Exo-MDPs, characterized by a partition of the state space into two components. The exogenous states evolve stochastically in a manner not affected by the agent's actions, whereas the endogenous states are affected by the actions, and evolve in a deterministic and known way conditional on the exogenous states. Exo-MDPs are a natural model for various applications including inventory control, finance, power systems, ride sharing, among others. Despite seeming restrictive, this work establishes that any discrete MDP can be represented as an Exo-MDP. Further, Exo-MDPs induce a natural representation of the transition and reward dynamics as linear functions of the exogenous state distribution. This linear representation leads to near-optimal algorithms with regret guarantees scaling only with the (effective) size of the exogenous state space $d$, independent of the sizes of the endogenous state and action spaces. Specifically, when the exogenous state is fully observed, a simple plug-in approach achieves a regret upper bound of $O(H^{3/2}\sqrt{dK})$, where $H$ denotes the horizon and $K$ denotes the total number of episodes. When the exogenous state is unobserved, the linear representation leads to a regret upper bound of $O(H^{3/2}d\sqrt{K})$. We also establish a nearly matching regret lower bound of $\Omega(Hd\sqrt{K})$ for the no observation regime. We complement our theoretical findings with an experimental study on inventory control problems.

Online Fair Allocation of Perishable Resources

We consider a practically motivated variant of the canonical online fair allocation problem: a decision-maker has a budget of perishable resources to allocate over a fixed number of rounds. Each round sees a random number of arrivals, and the decision-maker must commit to an allocation for these individuals before moving on to the next round. The goal is to construct a sequence of allocations that is envy-free and efficient. Our work makes two important contributions toward this problem: we first derive strong lower bounds on the optimal envy-efficiency trade-off that demonstrate that a decision-maker is fundamentally limited in what she can hope to achieve relative to the no-perishing setting; we then design an algorithm achieving these lower bounds which takes as input $(i)$ a prediction of the perishing order, and $(ii)$ a desired bound on envy. Given the remaining budget in each period, the algorithm uses forecasts of future demand and perishing to adaptively choose one of two carefully constructed guardrail quantities. We demonstrate our algorithm's strong numerical performance - and state-of-the-art, perishing-agnostic algorithms' inefficacy - on simulations calibrated to a real-world dataset.

Artificial Replay: A Meta-Algorithm for Harnessing Historical Data in Bandits

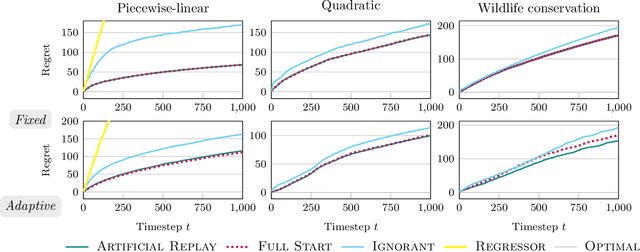
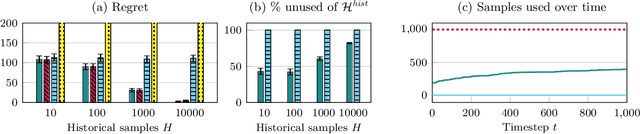
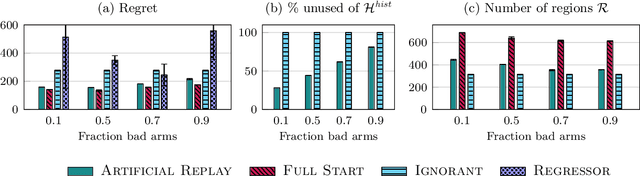
While standard bandit algorithms sometimes incur high regret, their performance can be greatly improved by "warm starting" with historical data. Unfortunately, how best to incorporate historical data is unclear: naively initializing reward estimates using all historical samples can suffer from spurious data and imbalanced data coverage, leading to computational and storage issues - particularly in continuous action spaces. We address these two challenges by proposing Artificial Replay, a meta-algorithm for incorporating historical data into any arbitrary base bandit algorithm. Artificial Replay uses only a subset of the historical data as needed to reduce computation and storage. We show that for a broad class of base algorithms that satisfy independence of irrelevant data (IIData), a novel property that we introduce, our method achieves equal regret as a full warm-start approach while potentially using only a fraction of the historical data. We complement these theoretical results with a case study of $K$-armed and continuous combinatorial bandit algorithms, including on a green security domain using real poaching data, to show the practical benefits of Artificial Replay in achieving optimal regret alongside low computational and storage costs.

Hindsight Learning for MDPs with Exogenous Inputs

We develop a reinforcement learning (RL) framework for applications that deal with sequential decisions and exogenous uncertainty, such as resource allocation and inventory management. In these applications, the uncertainty is only due to exogenous variables like future demands. A popular approach is to predict the exogenous variables using historical data and then plan with the predictions. However, this indirect approach requires high-fidelity modeling of the exogenous process to guarantee good downstream decision-making, which can be impractical when the exogenous process is complex. In this work we propose an alternative approach based on hindsight learning which sidesteps modeling the exogenous process. Our key insight is that, unlike Sim2Real RL, we can revisit past decisions in the historical data and derive counterfactual consequences for other actions in these applications. Our framework uses hindsight-optimal actions as the policy training signal and has strong theoretical guarantees on decision-making performance. We develop an algorithm using our framework to allocate compute resources for real-world Microsoft Azure workloads. The results show our approach learns better policies than domain-specific heuristics and Sim2Real RL baselines.

Adaptive Discretization in Online Reinforcement Learning

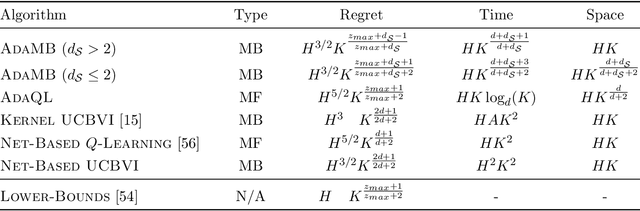
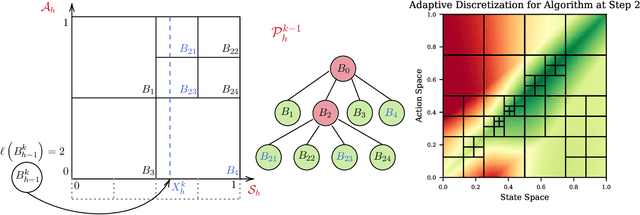
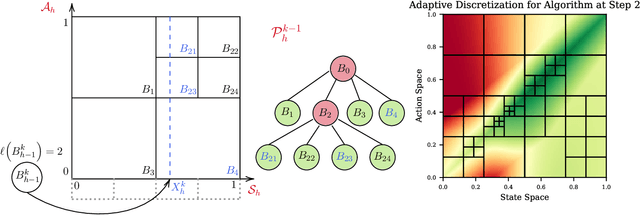
Discretization based approaches to solving online reinforcement learning problems have been studied extensively in practice on applications ranging from resource allocation to cache management. Two major questions in designing discretization-based algorithms are how to create the discretization and when to refine it. While there have been several experimental results investigating heuristic solutions to these questions, there has been little theoretical treatment. In this paper we provide a unified theoretical analysis of tree-based hierarchical partitioning methods for online reinforcement learning, providing model-free and model-based algorithms. We show how our algorithms are able to take advantage of inherent structure of the problem by providing guarantees that scale with respect to the 'zooming dimension' instead of the ambient dimension, an instance-dependent quantity measuring the benignness of the optimal $Q_h^\star$ function. Many applications in computing systems and operations research requires algorithms that compete on three facets: low sample complexity, mild storage requirements, and low computational burden. Our algorithms are easily adapted to operating constraints, and our theory provides explicit bounds across each of the three facets. This motivates its use in practical applications as our approach automatically adapts to underlying problem structure even when very little is known a priori about the system.

Adaptive Discretization for Model-Based Reinforcement Learning

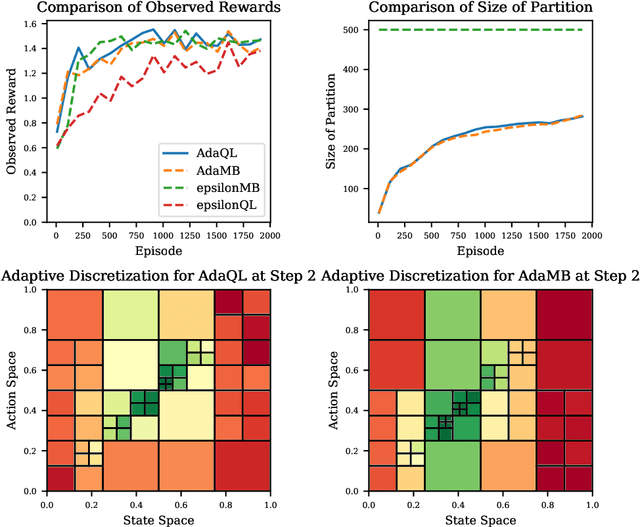
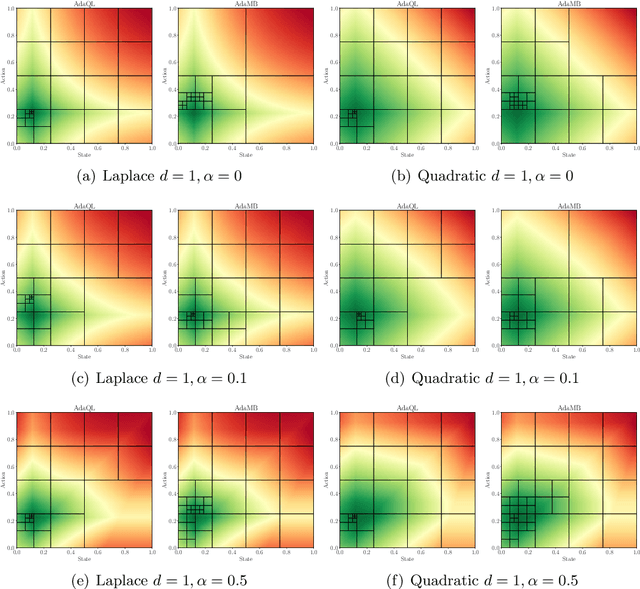
We introduce the technique of adaptive discretization to design efficient model-based episodic reinforcement learning algorithms in large (potentially continuous) state-action spaces. Our algorithm is based on optimistic one-step value iteration extended to maintain an adaptive discretization of the space. From a theoretical perspective, we provide worst-case regret bounds for our algorithm, which are competitive compared to the state-of-the-art model-based algorithms; moreover, our bounds are obtained via a modular proof technique, which can potentially extend to incorporate additional structure on the problem. From an implementation standpoint, our algorithm has much lower storage and computational requirements, due to maintaining a more efficient partition of the state and action spaces. We illustrate this via experiments on several canonical control problems, which shows that our algorithm empirically performs significantly better than fixed discretization in terms of both faster convergence and lower memory usage. Interestingly, we observe empirically that while fixed-discretization model-based algorithms vastly outperform their model-free counterparts, the two achieve comparable performance with adaptive discretization.